Towards the end of their evolution, stars with masses greater than
about ![]() explode, producing one of the most energetic
observable events in our Galaxy and external galaxies. The generally
accepted sequence of events leading to this outcome is as follows. A
star is said to have formed when a self-gravitating cloud of gas
(mostly hydrogen) collapses under its own gravity to densities and
temperatures at which, hydrogen burning begins. Under the action of
gravity, the centre gets denser and hotter resulting into a well
defined series of nuclear reactions. These reactions, starting from
hydrogen burning and going all the way to the formation of iron, start
at the centre and feed on the products of earlier reactions, which
continue to occur further out. With time, a series of concentric
shells are formed around the core, consisting of various elements
produced in the these reactions. This model is usually referred to as
the ``onion-skin model'' with a core of iron surrounded by shells of
lighter elements with the outer most shell consisting of hydrogen (and
possibly some He, Ne, O, N and C). Simulations show that, depending
upon the initial masses, some stars complete the full sequence of
nuclear reactions while for others this sequence is interrupted
(Woosley & Weaver1986; Trimble1982, and references therein).
Single stars with initial masses greater than about
explode, producing one of the most energetic
observable events in our Galaxy and external galaxies. The generally
accepted sequence of events leading to this outcome is as follows. A
star is said to have formed when a self-gravitating cloud of gas
(mostly hydrogen) collapses under its own gravity to densities and
temperatures at which, hydrogen burning begins. Under the action of
gravity, the centre gets denser and hotter resulting into a well
defined series of nuclear reactions. These reactions, starting from
hydrogen burning and going all the way to the formation of iron, start
at the centre and feed on the products of earlier reactions, which
continue to occur further out. With time, a series of concentric
shells are formed around the core, consisting of various elements
produced in the these reactions. This model is usually referred to as
the ``onion-skin model'' with a core of iron surrounded by shells of
lighter elements with the outer most shell consisting of hydrogen (and
possibly some He, Ne, O, N and C). Simulations show that, depending
upon the initial masses, some stars complete the full sequence of
nuclear reactions while for others this sequence is interrupted
(Woosley & Weaver1986; Trimble1982, and references therein).
Single stars with initial masses greater than about
![]() , explode
producing Type II supernovae (SNe) which are characterized by the
presence of hydrogen lines in their spectra and are usually found in
the spiral arms for spiral galaxies. Type I SNe on the other hand are
produced due to a white dwarf reaching the critical mass due to
accretion from a companion star in a binary system. These SNe are
devoid of hydrogen lines in their spectra and occur in all types of
galaxies. The star is completely disrupted in the case of Type I SNe
and no compact core remains (Woosley & Weaver1986). The
central part of the iron core in Type II SNe, however, is compressed
to nuclear densities and is left behind as a spinning degenerate
neutron star, which is, in some cases, detected as a pulsar. After
the core collapse, the rest of the material which is still in-falling,
rebounds (since the neutron core cannot be further compressed)
creating a powerful shock wave which ploughs though the the outer
layers of the star and finally emerges out of the circumstellar
material. The core collapse releases
, explode
producing Type II supernovae (SNe) which are characterized by the
presence of hydrogen lines in their spectra and are usually found in
the spiral arms for spiral galaxies. Type I SNe on the other hand are
produced due to a white dwarf reaching the critical mass due to
accretion from a companion star in a binary system. These SNe are
devoid of hydrogen lines in their spectra and occur in all types of
galaxies. The star is completely disrupted in the case of Type I SNe
and no compact core remains (Woosley & Weaver1986). The
central part of the iron core in Type II SNe, however, is compressed
to nuclear densities and is left behind as a spinning degenerate
neutron star, which is, in some cases, detected as a pulsar. After
the core collapse, the rest of the material which is still in-falling,
rebounds (since the neutron core cannot be further compressed)
creating a powerful shock wave which ploughs though the the outer
layers of the star and finally emerges out of the circumstellar
material. The core collapse releases ![]() erg of gravitational
energy in the form of neutrinos which, along with the blast wave,
couple with the outer layers and eject them at high speeds. The
explosion in both types of SNe releases
erg of gravitational
energy in the form of neutrinos which, along with the blast wave,
couple with the outer layers and eject them at high speeds. The
explosion in both types of SNe releases
![]() erg of kinetic
energy, which produces a shock wave travelling outwards. The cores of
massive stars with initial masses in the range of
erg of kinetic
energy, which produces a shock wave travelling outwards. The cores of
massive stars with initial masses in the range of
![]() can
also first explode as SNe and then collapse into low mass black holes
(Brown & Bethe1994). In such an event, a heavy star collapses
into a black hole without returning matter to the galaxy. The
empirical value of
can
also first explode as SNe and then collapse into low mass black holes
(Brown & Bethe1994). In such an event, a heavy star collapses
into a black hole without returning matter to the galaxy. The
empirical value of
![]() (the relative helium to metal
enrichment) implies a maximum mass of the star, after which the
nucleosynthesis must cut off (i.e., stars more massive than this limit
cannot contribute higher metals to the galaxy). This maximum mass
limit derived from the value of
(the relative helium to metal
enrichment) implies a maximum mass of the star, after which the
nucleosynthesis must cut off (i.e., stars more massive than this limit
cannot contribute higher metals to the galaxy). This maximum mass
limit derived from the value of
![]() and that derived
from the computation by Brown & Bethe (1994) are in good
agreement.
and that derived
from the computation by Brown & Bethe (1994) are in good
agreement.
![\includegraphics[scale=0.8]{RSN_light_curve.ps}](img37.png)
|
The interaction of the above shock wave with the in-falling circumstellar material produces the initial radiation, which announces the onset of the explosive event to observers on Earth. The shape of the initial optical light curve and the spectra at the peak of optical emission can be used to differentiate between the Type I and Type II SNe (Weiler & Sramek1988). Type-I SNe are characterized by the absence of hydrogen lines in their peak optical spectra while Type-II exhibit hydrogen lines in their spectra. Based on further finer details of the light curve, SNe are further sub-divided into Type Ia, Ib, II-L (linear) and II-P (plateau). However, initial radio emission has been detected from Type-Ia SNe. The optical light curve of Type II-L decreases monotonically in intensity after reaching a peak value while that of Type II-P, on the other hand goes through a flat plateau before starting to decay further. The peak absolute blue magnitude of Type Ia SNe has been found to be remarkably constant for different events; these can hence be used as ideal standard candles in the universe. Hubble constant can therefore be derived from the observations of extragalactic Type Ia SNe light curves. It is this property of Type Ia SNe which is responsible for the currently thriving industry of Supernova Cosmology (Branch1998, and references therein).
Typically, radio emission is first detected at higher frequencies, and
later, at successively lower frequencies due to changes in the optical
depth for external free-free absorption (Weiler et al.1986). A
typical example of radio light curve for a Type II-L SN is shown in
Fig. 1.1. The shape and spectral behavior of this
initial radio light curve is thought to be typical of the class.
Radio emission is detected significantly after the optical light is
detected. The spectral index ![]() (
(
![]() )
evolves from a value of
)
evolves from a value of ![]() to a relatively constant value of
to a relatively constant value of
![]() when the emitting region becomes optically thin for radio
photons (Fig. 1.2). Observations of SN1983N, a Type Ib
SN, on the other hand, exhibited a far more rapid rise as well as
decay in the flux density compared to that of Type II-L SN. This
difference in the radio light curves of the two types have been
interpreted as being due to significant differences between the
environments of Type Ib and II-L SNe.
when the emitting region becomes optically thin for radio
photons (Fig. 1.2). Observations of SN1983N, a Type Ib
SN, on the other hand, exhibited a far more rapid rise as well as
decay in the flux density compared to that of Type II-L SN. This
difference in the radio light curves of the two types have been
interpreted as being due to significant differences between the
environments of Type Ib and II-L SNe.
After the blast wave crosses the denser circumstellar envelope into
the more tenuous interstellar medium (ISM), this initial radio
emission ultimately dies down, over time scales of several weeks for
Type I SNe to many years for Type II SNe. The evolution of the blast
wave as it ploughs though the ISM can be roughly described in four
distinct stages (Reynolds & Chevalier1984). This interaction of
the blast wave with the ISM, at much later times, produces sources of
synchrotron emission in the sky, called Supernova Remnants (SNRs).
SNRs are visible at radio bands (and at optical and X-ray bands in
regions where the obscuration by the Galactic plane is relatively low)
for up to
![]() years after the initial explosion. This
dissertation is concerned with the observations of such Galactic SNRs
at low radio frequencies.
years after the initial explosion. This
dissertation is concerned with the observations of such Galactic SNRs
at low radio frequencies.
![\includegraphics[scale=0.8]{RSN_SpNdx.ps}](img41.png)
|
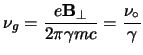 |
(4.1) |
| (4.2) |
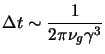 |
(4.3) |
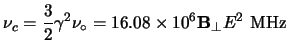 |
(4.4) |
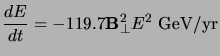 |
(4.5) |
For a homogeneous and isotropic ensemble of electrons with energy
density distribution ![]() , the total intensity will be given by
, the total intensity will be given by
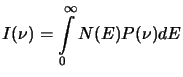 |
(4.6) |
Emission from a single electron will clearly be elliptically polarized with the electric field vector perpendicular to the projected magnetic field vector. However, for an ensemble of electrons with a random distribution of pitch angles, the observed radiation will be partially linearly polarized with the degree of polarization in a uniform magnetic field given by
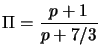 |
(4.8) |
A large number of SNRs are radio sources with only less than 30%
visible in optical and X-ray bands. The lack of optical and X-ray
radiation is primarily due to obscuration by the Galactic disk. Out
of the 225 Galactic SNRs listed in the catalogue of Galactic SNRs
(Green2000), about 80% are of shell-type morphology (see
Section 1.2.4) with a median size of ![]() arcmin.
The emission is polarized (fractional polarization at
arcmin.
The emission is polarized (fractional polarization at ![]() level
for the shell-type SNRs and much higher for filled centre SNRs) with a
negative spectral index and is therefore believed to be synchrotron
radiation. These gross observed radio properties of the radio
emission from SNRs can be understood by modeling the shock wave as a
spherical supersonic piston propagating in a uniform medium (the ISM)
sweeping up the ISM mass as it moves. Its evolution is described as
four distinct stages (Reynolds1988, and references
therein):
level
for the shell-type SNRs and much higher for filled centre SNRs) with a
negative spectral index and is therefore believed to be synchrotron
radiation. These gross observed radio properties of the radio
emission from SNRs can be understood by modeling the shock wave as a
spherical supersonic piston propagating in a uniform medium (the ISM)
sweeping up the ISM mass as it moves. Its evolution is described as
four distinct stages (Reynolds1988, and references
therein):
In this stage of the evolution, the ejected mass ![]() is much
more than the mass swept-up by the shock front, i.e.
is much
more than the mass swept-up by the shock front, i.e.
![]() where
where ![]() is the shock radius and
is the shock radius and ![]() the
pre-shock density. The influence of the ISM on the dynamics of the
ejecta in this stage is negligible and the initial properties of the
explosion dominate the evolution. Consequently the blast wave
freely expands into the medium.
the
pre-shock density. The influence of the ISM on the dynamics of the
ejecta in this stage is negligible and the initial properties of the
explosion dominate the evolution. Consequently the blast wave
freely expands into the medium.
With time, the shock front sweeps up the ISM material and enters
this phase when the swept-up ISM mass is comparable to that of the
ejected mass. The shock is still strong and the pressure due to the
swept-up mass is negligible. The expansion is essentially adiabatic
(which is the other name this phase goes by) and the dynamical
evolution is given by Sedov (1959) solution for the dynamics
of a point explosion in a uniform medium. For a gas with the ratio
of specific heats of 5/3, the shock radius and velocity (![]() ) are
given by
) are
given by
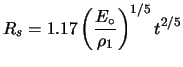 |
(4.9) |
| (4.10) |
Once the age of the remnant becomes comparable to the radiative cooling time scales near the shock, the blast wave enters the radiative phase. The deceleration becomes rapid and the shock compression becomes large. By this time, the dynamics and the resulting observed morphologies are significantly affected by the structure of the ISM, particularly the inhomogeneity of the ISM.
The time at which this phase begins and the shock velocity at this time is given by
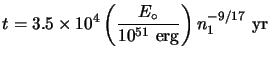 |
(4.11) |
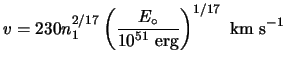 |
(4.12) |
Once the expansion velocity of the shock decreases below the local
sound speed, it dissipates and merges with the ISM on time scales of
![]() years.
years.
This simple model of a shock wave propagating in a uniform medium,
however, ignores a number of other effects such as dynamical effects
of the magnetic field, pressure forces in the radiative phase and
inhomogeneities in the ISM (Woltjer1972). Hydrodynamic
calculations show that SNe produce ejecta with a uniform density
towards the outer parts while the inner parts (close to the star) have
a steep density profile (like
![]() ). A reasonable
density profile for Type I SNe has a constant density ejecta for the
inner four-sevenths of the mass, and the outer three-sevenths obeying
). A reasonable
density profile for Type I SNe has a constant density ejecta for the
inner four-sevenths of the mass, and the outer three-sevenths obeying
![]() . Numerical simulations for Type I SNe with such
a density profile modified the evolution of the shock radius to
. Numerical simulations for Type I SNe with such
a density profile modified the evolution of the shock radius to
![]() when the Sedov phase is reached, which is closer to
the observed value of the exponent (e.g. for Tycho and SN 1006).
when the Sedov phase is reached, which is closer to
the observed value of the exponent (e.g. for Tycho and SN 1006).
As mentioned earlier, radio emission from SNRs is believed to be
synchrotron radiation which requires understanding of the origin of
the relativistic electrons and magnetic field. Broadly, the central
pulsar is thought to be the source of both these quantities for
Crab-like SNRs (see Section 1.2.4), while, for
shell-type SNRs, both come from the ambient ISM. The inferred
magnetic fields in SNRs, measured from the rotation measure
measurements of background radio sources, X-ray observations and
Zeeman splitting of OH maser lines (Brogan et al.2000), is however
![]() order of magnitude higher than the ambient magnetic field,
requiring magnetic field amplification mechanisms as well. Although
it is easy to imagine amplification of the frozen-in magnetic field in
the SNR shells, the observed brightness of young shell-type SNRs is
often more than can be explained by magnetic field amplification due
to compression by the shock alone (although, magnetic field strengths
measured for a few SNRs using the Zeeman splitting of OH (1720 MHz) lines
are consistent with the hypothesis that ambient molecular cloud
magnetic fields are compressed via the SNR shock to the observed
values (Brogan et al.2000)). The observationally deduced magnetic
field for Cas A is far too high to be explained by magnetic field
amplification by compression by a factor 4 compression. Similarly,
the deduced magnetic field for the shell-type Kepler's SNR
(Matsui et al.1984) is too high to be produced by the
amplification of the ambient field in the shock front. It is
therefore believed that for shell-type SNRs, a combination of particle
acceleration in the shock front (Bell1978a; Bell1978b) and
magnetic field amplification as well as particle acceleration behind
the shock (Cowsik & Sarkar1984; Gull1973) are responsible for the
observed radio brightness. On the other hand, the observed properties
and the evolution of Crab-type SNRs are believed to be dominated by
rotational energy loss from the central pulsar
(Reynolds & Chevalier1984).
order of magnitude higher than the ambient magnetic field,
requiring magnetic field amplification mechanisms as well. Although
it is easy to imagine amplification of the frozen-in magnetic field in
the SNR shells, the observed brightness of young shell-type SNRs is
often more than can be explained by magnetic field amplification due
to compression by the shock alone (although, magnetic field strengths
measured for a few SNRs using the Zeeman splitting of OH (1720 MHz) lines
are consistent with the hypothesis that ambient molecular cloud
magnetic fields are compressed via the SNR shock to the observed
values (Brogan et al.2000)). The observationally deduced magnetic
field for Cas A is far too high to be explained by magnetic field
amplification by compression by a factor 4 compression. Similarly,
the deduced magnetic field for the shell-type Kepler's SNR
(Matsui et al.1984) is too high to be produced by the
amplification of the ambient field in the shock front. It is
therefore believed that for shell-type SNRs, a combination of particle
acceleration in the shock front (Bell1978a; Bell1978b) and
magnetic field amplification as well as particle acceleration behind
the shock (Cowsik & Sarkar1984; Gull1973) are responsible for the
observed radio brightness. On the other hand, the observed properties
and the evolution of Crab-type SNRs are believed to be dominated by
rotational energy loss from the central pulsar
(Reynolds & Chevalier1984).
Two classes of electron acceleration mechanisms have been used: turbulent acceleration at the unstable contact discontinuity and acceleration in the shock front itself. The first mechanism uses ``second-order Fermi acceleration'' and explains the morphology and emission from SNRs like Cas A. The latter mechanism uses the more efficient ``first-order Fermi acceleration''. This has the added advantage that the inferred electron energy spectra is naturally a power law and explains the morphology and the spectra of typical shell-type SNRs (Reynolds & Ellison1992). Mechanisms for magnetic field amplification are however far less well understood. Magnetic fields measured in a few SNRs are much too high to be explained by compression alone. Observed magnetic fields which are predominantly radial in young SNRs (Dickel & Milne1976) also argue against the amplified field being the swept-up ambient field. Magnetic field amplification in the Rayleigh-Taylor instability due to the deceleration of the ejecta (Jun et al.1996; Jun & Norman1996b; Jun & Norman1996a), is an attractive model, especially for clumpy ejecta and/or circulstellar medium in the sense that it can explain the mostly radial orientation of the magnetic field in the SNR shells. Their simulation also shows that such magnetic field amplification is dependent on the orientation of the field and can produce morphologies similar to those of ``barrel-shaped'' SNRs.
Although the details of the particle acceleration and magnetic field
amplification mechanism are still not well understood, it is clear
from the observed data that the radio emission from SNRs is
synchrotron radiation. Radio emission from SNRs above ![]() MHz
has a non-thermal spectrum (Equation 1.7) and
significant linear polarization (
MHz
has a non-thermal spectrum (Equation 1.7) and
significant linear polarization (![]() % for shell-type SNRs and up
to 30% for filled centre SNRs). Both these gross properties are
considered to be defining properties of synchrotron emission.
Integrated continuum radio spectra are therefore the primary
signatures used to identify SNRs. As is also obvious, SNRs also
produce sources of extended emission. Radio SNRs are classified into
roughly four categories (see Section 1.2.4) based on
the radio morphology. Radio morphology also provides information
about the SNR type, its interaction with the ambient ISM as well as
with the ambient magnetic field (Dickel & Milne1976). Candidate
SNRs are therefore often identified from single frequency observations
based on the morphological evidence. However, H II regions in the
Galaxy also exhibit extended radio emission easily detected at higher
frequencies and, in some cases even exhibit morphologies similar to
those of SNRs. Identifications of SNRs based on a single high
frequency observation are therefore unreliable; observations at at
least two frequencies are therefore usually required for proper
identification of extended radio sources, to get a handle on the
spectral index. Non-detection of thermal infrared emission, and where
possible, lack of radio recombination lines (RRLs) are also used as
supporting evidences to distinguish synchrotron sources from sources
of thermal emission. However, RRL observations in the Galaxy are
usually at coarse resolution and have a patchy coverage of the
Galactic plane. High frequency observations in the Galactic plane
also suffer from contaminating thermal emission (see
Section 1.2.3), which has a relatively flat spectrum
above
% for shell-type SNRs and up
to 30% for filled centre SNRs). Both these gross properties are
considered to be defining properties of synchrotron emission.
Integrated continuum radio spectra are therefore the primary
signatures used to identify SNRs. As is also obvious, SNRs also
produce sources of extended emission. Radio SNRs are classified into
roughly four categories (see Section 1.2.4) based on
the radio morphology. Radio morphology also provides information
about the SNR type, its interaction with the ambient ISM as well as
with the ambient magnetic field (Dickel & Milne1976). Candidate
SNRs are therefore often identified from single frequency observations
based on the morphological evidence. However, H II regions in the
Galaxy also exhibit extended radio emission easily detected at higher
frequencies and, in some cases even exhibit morphologies similar to
those of SNRs. Identifications of SNRs based on a single high
frequency observation are therefore unreliable; observations at at
least two frequencies are therefore usually required for proper
identification of extended radio sources, to get a handle on the
spectral index. Non-detection of thermal infrared emission, and where
possible, lack of radio recombination lines (RRLs) are also used as
supporting evidences to distinguish synchrotron sources from sources
of thermal emission. However, RRL observations in the Galaxy are
usually at coarse resolution and have a patchy coverage of the
Galactic plane. High frequency observations in the Galactic plane
also suffer from contaminating thermal emission (see
Section 1.2.3), which has a relatively flat spectrum
above ![]() GHz. Below this frequency, typical thermal emission
strongly turns over due to free-free absorption. Synchrotron emission
on the other hand, has a negative spectral index for a large range of
frequencies. As a result, the emission from SNRs is usually stronger
at lower frequencies while the thermal emission is severely
diminished. For these reasons, high resolution observations at low
frequencies where the non-thermal emission is stronger than the
thermal emission can identify SNRs unambiguously and also measure
spatially resolved brightness variations. The latter provide crucial
information about the interaction of the blast wave with the ISM as
well about particle acceleration/magnetic field amplification.
GHz. Below this frequency, typical thermal emission
strongly turns over due to free-free absorption. Synchrotron emission
on the other hand, has a negative spectral index for a large range of
frequencies. As a result, the emission from SNRs is usually stronger
at lower frequencies while the thermal emission is severely
diminished. For these reasons, high resolution observations at low
frequencies where the non-thermal emission is stronger than the
thermal emission can identify SNRs unambiguously and also measure
spatially resolved brightness variations. The latter provide crucial
information about the interaction of the blast wave with the ISM as
well about particle acceleration/magnetic field amplification.
The spectral index depends on the kinetic energy input mechanism (e.g.
turbulence in the shells of shell-type SNRs and the central pulsar in
Crab-type SNRs), localized particle acceleration mechanisms
(e.g. interaction of the shock front with higher density ISM) and the
properties of the intervening ISM (e.g. differential free-free
absorption across SNRs). About 80% of the known Galactic SNRs are of
shell-type (Green2000) and exhibit a broad range of spectral
indices (
![]() ) with a mean value of
) with a mean value of ![]() .
This implies a mean electron energy spectrum
.
This implies a mean electron energy spectrum
![]() , close
to what is expected from theoretical models for acceleration in strong
shocks. Implied electron energy spectra corresponding to the lower
range of
, close
to what is expected from theoretical models for acceleration in strong
shocks. Implied electron energy spectra corresponding to the lower
range of ![]() are explained by attributing them to weaker shocks
while those corresponding to the higher range require the inclusion of
non-linear effects. Data also suggests a trend in the spectral index
with the remnant age (i.e. with diameter). Smaller diameter SNRs,
considered to be younger, have
are explained by attributing them to weaker shocks
while those corresponding to the higher range require the inclusion of
non-linear effects. Data also suggests a trend in the spectral index
with the remnant age (i.e. with diameter). Smaller diameter SNRs,
considered to be younger, have
![]() while older, larger
diameter SNRs have flatter spectra. However it must also be kept in
mind that the measured diameter is subject to (often large) errors in
the distance estimate. Even if the distance is well known, the
diameter of the SNR can be strongly influenced by the properties of
the progenitor star and the local ISM and the inferred age may be
quite different from the true age. Spectral indices for most SNRs
have been obtained from measurements carried out with a variety of
telescopes and techniques, resulting into uncertainties in flux
density scales. As a result, the spectral indices are seldom known to
accuracies better than
while older, larger
diameter SNRs have flatter spectra. However it must also be kept in
mind that the measured diameter is subject to (often large) errors in
the distance estimate. Even if the distance is well known, the
diameter of the SNR can be strongly influenced by the properties of
the progenitor star and the local ISM and the inferred age may be
quite different from the true age. Spectral indices for most SNRs
have been obtained from measurements carried out with a variety of
telescopes and techniques, resulting into uncertainties in flux
density scales. As a result, the spectral indices are seldom known to
accuracies better than ![]() .
.
Measurements of spatial and/or temporal variations in the radio
spectra of SNRs are probably the best way to study the nature of
electron acceleration mechanisms. Spatial spectral variations provide
information about the local dynamics and require spatially resolved
observations at at least at two frequencies. High resolution
observations are usually done using interferometric telescopes.
However, the set of the spatial frequencies measured by such
instruments with fixed physical separation between the antennas are a
function of the observing frequency. As a result the spatial
frequencies sampled at two different frequencies are in general
different and dividing the two images at different frequencies to
obtain spectral index maps produces artifacts. In telescopes like the
Very Large Array (VLA) this problem is solved by scaling the array in
proportion to the observing frequency, but for most other
interferometric telescopes, this remains a problem. Observations with
interferometric telescopes also suffer from missing larger scale
emission which in turn result into differences in flux density
base-level. Similarly, single dish observations also suffer from
base-level problems due to very large scale background emission within
the field of view of the telescope. To minimize the errors in the
measurement of spectral index due to these effects,
Anderson & Rudnick (1993) used the so called ``T-T plot'' to
measure the local gradient in the maps at two frequencies. This
method is insensitive to large scale base-level variations in the two
maps and gives a more reliable spatially resolved spectral index
measurement. They find a spatial variation from ![]() to
to ![]() across a few, hopefully representative, SNRs. More recently
Katz-Stone et al. (2000a) used the method of spectral tomography to
measure spectral variations within Tycho's SNR. They identified a
number of filaments with spectral index different from that of the
smoother background. The filaments in the outer rim show a trend such
that brighter filaments have a flatter spectral index which could be
due to the interaction of the blast wave with a inhomogeneous ambient
medium or due to inhomogeneities in the magnetic field.
across a few, hopefully representative, SNRs. More recently
Katz-Stone et al. (2000a) used the method of spectral tomography to
measure spectral variations within Tycho's SNR. They identified a
number of filaments with spectral index different from that of the
smoother background. The filaments in the outer rim show a trend such
that brighter filaments have a flatter spectral index which could be
due to the interaction of the blast wave with a inhomogeneous ambient
medium or due to inhomogeneities in the magnetic field.
![\includegraphics[scale=0.8]{G043.3-0.2.epsi}](img98.png)
|
In their classic papers on the measurement of low-frequency continuum
spectra of Galactic supernova remnants, Dulk & Slee (1975)
reported spectral turnovers in several SNRs in the galactic plane at
low frequencies. Such a turnover in the spectra of SNRs has since
been confirmed by more extensive measurements at ![]() MHz
(Kassim1989). The spectral index above
MHz
(Kassim1989). The spectral index above ![]() MHz is
negative and is typical of most SNRs
(Fig.1.34.1). The spectra however turns-over below this frequency
due to absorption by low density ionized gas in the intervening ISM
(Kassim1989). The observed flux density at a frequency
MHz is
negative and is typical of most SNRs
(Fig.1.34.1). The spectra however turns-over below this frequency
due to absorption by low density ionized gas in the intervening ISM
(Kassim1989). The observed flux density at a frequency ![]() in the presence of absorbing foreground medium of free-free optical
depth
in the presence of absorbing foreground medium of free-free optical
depth
![]() at a reference frequency
at a reference frequency ![]() can be
written as
can be
written as
| (4.14) |
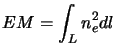 |
(4.15) |
Evidence for the existence of a widespread low-density ionized
component in the inner Galaxy has come from observations of radio
recombination lines (RRLs) near 1400 MHz (Heiles et al.1996; Hart & Pedlar1976; Lockman1980) and near 327 MHz
(Anantharamaiah1985b; Roshi & Anantharamaiah2000). These RRLs have been detected at
almost every observed position in the inner Galaxy (with
![]() and
and
![]() ) including those positions where there are no
discrete radio continuum sources (i.e. blank regions). This is
believed to be the extended H II region envelopes (EHEs)
(Anantharamaiah1985a). The parameters of the gas derived from the
RRL observations are
) including those positions where there are no
discrete radio continuum sources (i.e. blank regions). This is
believed to be the extended H II region envelopes (EHEs)
(Anantharamaiah1985a). The parameters of the gas derived from the
RRL observations are
![]() K,
K,
![]() cm
cm![]() ,
with a filling factor of
,
with a filling factor of ![]() . Based on the statistics of spectral
turnovers in a number of SNRs and the properties of the low-density
envelopes derived using RRL data, Kassim (1989) has argued in
favor of a connection between the RRL-gas and the free-free-absorbing
gas towards SNRs. The optical depth towards a few SNRs inferred from
the low frequency spectral turn over and that from RRL observations
agree well with each other, lending support to this suggestion. On
the theoretical front, McKee & Williams (1997) considered the
luminosity function of OB associations in the Galaxy and found that
about 65% of the ionizing photons emitted by O and B stars are
absorbed outside the known HII regions. About 10% of these photons
are needed to maintain the Warm Ionized Medium (WIM). The majority of
the escaping photons can thus generate large HII envelopes. These HII
envelopes are thus a reservoir of more than 50% of the ionizing
photons emitted by all the O and B stars. An understanding of the
properties of this ionized component is thus important in the galactic
context. However the evidence remains circumstantial. The resolution
of the low frequency RRL observations was too coarse to localize the
source of RRL emission. High resolution RRL observation towards SNRs
which do show spatially resolved low frequency absorption will provide
a direct test for this. The Giant Meterwave Radio Telescope (GMRT)
offers the right range of frequencies, resolution and sensitivity for
these observations and is an ideal instrument for such a study.
. Based on the statistics of spectral
turnovers in a number of SNRs and the properties of the low-density
envelopes derived using RRL data, Kassim (1989) has argued in
favor of a connection between the RRL-gas and the free-free-absorbing
gas towards SNRs. The optical depth towards a few SNRs inferred from
the low frequency spectral turn over and that from RRL observations
agree well with each other, lending support to this suggestion. On
the theoretical front, McKee & Williams (1997) considered the
luminosity function of OB associations in the Galaxy and found that
about 65% of the ionizing photons emitted by O and B stars are
absorbed outside the known HII regions. About 10% of these photons
are needed to maintain the Warm Ionized Medium (WIM). The majority of
the escaping photons can thus generate large HII envelopes. These HII
envelopes are thus a reservoir of more than 50% of the ionizing
photons emitted by all the O and B stars. An understanding of the
properties of this ionized component is thus important in the galactic
context. However the evidence remains circumstantial. The resolution
of the low frequency RRL observations was too coarse to localize the
source of RRL emission. High resolution RRL observation towards SNRs
which do show spatially resolved low frequency absorption will provide
a direct test for this. The Giant Meterwave Radio Telescope (GMRT)
offers the right range of frequencies, resolution and sensitivity for
these observations and is an ideal instrument for such a study.
Apart from non-thermal emission, the Galactic plane, particularly at low Galactic latitudes, is also a sources of significant radio emission with a thermal spectrum. This emission is from H II regions and planetary nebulae in the Galaxy and is caused by the interaction between free charged particles, referred to as free-free or thermal bremsstrahlung emission.
The observed intensity from an emitting region of linear size ![]() with
a foreground radiation intensity of
with
a foreground radiation intensity of ![]() and background intensity
of
and background intensity
of ![]() is given by
is given by
A charged particle moving in the electric field of another charged
particle undergoes a change in its direction of motion. This change
of direction requires acceleration and as a result the particle emits
electromagnetic radiation. In a realistic situation, however, there
is a distribution of particle velocities and the total radiation is
determined by integrating the emission during one interaction over the
velocity distribution. To compute this, it is assumed (1) that the
electric field in which the particle is moving is effective only over
a finite distance, (2) that the radiated energy is small compared to
the kinetic energy of the moving particle (i.e. the encounter is
adiabatic) and (3) the period of the emitted wave is small compared to
the duration of the encounter. For a Maxwellian velocity
distribution,
![]() where
where
![]() is the Plank function. For
is the Plank function. For
![]() , this can be approximated by
, this can be approximated by
![]() - the usual Rayleigh-Jeans
approximation. For a source of homogeneous density and temperature
with
- the usual Rayleigh-Jeans
approximation. For a source of homogeneous density and temperature
with ![]() , and using the Rayleigh-Jeans approximation,
Equation 1.16 can be written as
, and using the Rayleigh-Jeans approximation,
Equation 1.16 can be written as
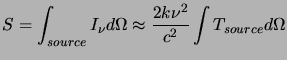 |
(4.18) |
From the point of view of radio study of SNRs, the important point to
note is that thermal emission progressively diminishes at frequencies
below ![]() GHz while the non-thermal emission progressively
becomes stronger in this range of frequencies. Strong emission from
H II regions has been observed all along the Galactic plane. High
frequency observations close to or above this frequency are more
sensitive to thermal emission and not well suited to the study of
SNRs which emit non-thermal radiation at radio bands. On the other
hand, at lower frequencies, thermal emission is diminished while
non-thermal emission from SNRs progressively becomes stronger (see
Fig. 5.15). Low frequency observations, where the
contamination from thermal emission is minimized, are therefore more
suited for the study of SNRs.
GHz while the non-thermal emission progressively
becomes stronger in this range of frequencies. Strong emission from
H II regions has been observed all along the Galactic plane. High
frequency observations close to or above this frequency are more
sensitive to thermal emission and not well suited to the study of
SNRs which emit non-thermal radiation at radio bands. On the other
hand, at lower frequencies, thermal emission is diminished while
non-thermal emission from SNRs progressively becomes stronger (see
Fig. 5.15). Low frequency observations, where the
contamination from thermal emission is minimized, are therefore more
suited for the study of SNRs.
As mentioned above, angular resolution is important from the point of view of SNR identification and other detailed studies (particle acceleration, interaction with the local ISM, brightness variation as a function of galactic latitude, etc.). Since emission in the galactic plane occurs at all angular scales, it is also important that the observations be sensitive to large scale emission. To meet the requirement of high angular resolution with sensitivity to large scale emission, many observations of SNRs have been done at high frequencies either single dish instruments (Clark et al.1975b; Duncan et al.1997b; Clark et al.1975a; Duncan et al.1997a) or using interferometric telescopes (Gray1994b; Gray1994a; Kesteven & Caswell1987; Whiteoak & Green1996). However the uv-coverage of these interferometric observations was not good resulting into severe artifacts in the images. Also, these observations often suffer from contamination by thermal emission, particularly for fields in the Galactic plane.
The GMRT, operating at 150, 233, 327, 610 and 1400 MHz provides
frequency coverage where, typically, non-thermal emission is dominant.
With a shortest physical antenna separation of ![]() m and
largest separation of
m and
largest separation of ![]() km, it also provides high angular
resolution at these low frequencies (
km, it also provides high angular
resolution at these low frequencies (![]() arcsec to
arcsec to
![]() arcsec) while remaining sensitive to emission at large angular
scales (
arcsec) while remaining sensitive to emission at large angular
scales (
![]() to
to ![]() arcmin). With a large collecting
area, GMRT offers many advantages for the study of Galactic
non-thermal emission in general and SNRs in particular. High
resolution multi-frequency mapping of the galactic plane will also
make it possible to identify compact sources of non-thermal emission
(possibly compact SNRs) which may be confused with compact thermal
sources in high frequency observations.
arcmin). With a large collecting
area, GMRT offers many advantages for the study of Galactic
non-thermal emission in general and SNRs in particular. High
resolution multi-frequency mapping of the galactic plane will also
make it possible to identify compact sources of non-thermal emission
(possibly compact SNRs) which may be confused with compact thermal
sources in high frequency observations.
The gross morphology of SNRs is largely governed by (1) properties of the progenitor and the pre-supernova circumstellar environment and (2) properties of the local interstellar medium and magnetic field. Traditionally, Galactic SNRs are classified in four different categories namely (1) shell-type, (2) filled centre (or Crab-type), (3) composite and (4) barrel shaped. About 80% of the SNRs in the Galactic SNR catalogue compiled and maintained by Green (2000) exhibit what is referred to as the shell-type morphology. This is expected from the generic model of an isotropic blast wave ploughing though the ISM and producing a bubble of emission after it slows down, having gathered enough ISM mass at the shock front. In projection, the bubble appears as a ring or shell of emission. On the other hand Crab-type SNRs exhibit a nebula of flat spectrum emission and is believed to be powered by the central neutron star. Variations of these basic morphologies are produced either due to a difference in the progenitor or in the local interstellar environment. The observed properties of these classes of SNRs are also therefore characteristic of the class and are briefly described below.
As mentioned above, 80% of the known Galactic SNRs are of this type. Typical examples are Kepler's and Tycho's SNR, SN 1006 (Fig. 1.4). These SNRs are characterized by a ring of emission which is often incomplete. As the blast wave decelerates, it enters the radiative phase of its evolution. The contact discontinuity between the shock front and the shocked medium is unstable and produces a thin shell of turbulence. The turbulence in the shell is believed to be the source of particle acceleration within the shell and magnetic field amplification by turbulent mixing (Chevalier1982). A reverse shock develops just behind the shell and moves into the out-flowing ejecta, heating it to sufficiently high temperatures to produce the observed X-ray emission (Chevalier & Fransson1994).
![\includegraphics[scale=0.5]{SN1006.rot90.ps}](img154.png)
|
The typical average spectral index ![]() along the shell ranges
from
along the shell ranges
from ![]() to
to ![]() . In some of the sensitive images of shell-type
SNRs, weak emission (from the bubble) is sometimes seen in projection,
filling the interior of the ring. The spectral index of this emission
and the ring is, however the same, indicating that this corresponds to
the bubble of emission seen projected at the centre of the shell.
Substantial variation in the brightness across the shell of emission
is often seen and may be due to the inhomogeneity of the local ISM
with which the shock front interacts. This also produces spectral
index variations in some cases (Anderson & Rudnick1993)
indicating sites of enhanced particle acceleration or magnetic field
amplification. The emission from the shell is linearly polarized at
. In some of the sensitive images of shell-type
SNRs, weak emission (from the bubble) is sometimes seen in projection,
filling the interior of the ring. The spectral index of this emission
and the ring is, however the same, indicating that this corresponds to
the bubble of emission seen projected at the centre of the shell.
Substantial variation in the brightness across the shell of emission
is often seen and may be due to the inhomogeneity of the local ISM
with which the shock front interacts. This also produces spectral
index variations in some cases (Anderson & Rudnick1993)
indicating sites of enhanced particle acceleration or magnetic field
amplification. The emission from the shell is linearly polarized at
![]() level and the inferred projected magnetic field is usually
radial.
level and the inferred projected magnetic field is usually
radial.
These types of SNRs are characterized by a flat spectrum plerionic
emission (
![]() ) almost uniformly filling the emission
region. Less than 10% of the known Galactic SNRs are of this type.
Strong linear polarization up to 30% level has been observed from
such SNRs. A typical example of this class of SNRs, not
surprisingly, is the Crab SNR (Fig. 1.5) or 3C58.
Reynolds & Chevalier (1984) modeled a plerion as a spherical,
homogeneous bubble of relativistic particles and magnetic field
inflated by a central neutron star amidst uniformly expanding
supernova ejecta. The plerionic emission is believed to be driven
by the rotational energy losses of the central neutron star, which
is seen as a pulsar at the centre of the Crab nebula. The central
neutron star is believed to be the source of the magnetic field as
well as of the energy which accelerates the electron in the medium
thereby maintaining the flat spectrum of the emission. With the
advent of high resolution X-ray telescopes, many plerionic SNRs have
been found to be strong X-ray sources where the X-ray emission comes
from the central region.
) almost uniformly filling the emission
region. Less than 10% of the known Galactic SNRs are of this type.
Strong linear polarization up to 30% level has been observed from
such SNRs. A typical example of this class of SNRs, not
surprisingly, is the Crab SNR (Fig. 1.5) or 3C58.
Reynolds & Chevalier (1984) modeled a plerion as a spherical,
homogeneous bubble of relativistic particles and magnetic field
inflated by a central neutron star amidst uniformly expanding
supernova ejecta. The plerionic emission is believed to be driven
by the rotational energy losses of the central neutron star, which
is seen as a pulsar at the centre of the Crab nebula. The central
neutron star is believed to be the source of the magnetic field as
well as of the energy which accelerates the electron in the medium
thereby maintaining the flat spectrum of the emission. With the
advent of high resolution X-ray telescopes, many plerionic SNRs have
been found to be strong X-ray sources where the X-ray emission comes
from the central region.
![\includegraphics[scale=0.5]{CRAB.rot90.ps}](img158.png)
|
The blast wave should however produce a shell of emission outside such
a nebula where it interacts with the ISM. The existence of a
high-velocity, hydrogen-rich envelope corresponding to the initial
blast wave is also required to account for the low total mass and
kinetic energy of the observed nebula. No shell of emission has
however been detected for such SNRs - at least not at radio
frequencies. A deep search for the shell around the Crab nebula did
not reveal any shell emission and this has been interpreted as being
due to the blast wave expanding into a low density medium
(Frail et al.1995). The spectral index of the plerionic emission
for the Crab nebula is
![]() . If the shell is close to the
edge of the nebula, it can be distinguished from the nebula by the
change in the spectral index from this value to close to
. If the shell is close to the
edge of the nebula, it can be distinguished from the nebula by the
change in the spectral index from this value to close to ![]() ,
typical for shock accelerated shell emission. No evidence for a
significant change in the spectral index was found by these authors.
Similarly no such shell has been found in H
,
typical for shock accelerated shell emission. No evidence for a
significant change in the spectral index was found by these authors.
Similarly no such shell has been found in H![]() and X-ray emission
(Fesen et al.1997; Predehl & Schmitt1995). However, HST observations reveal a
thin shell of [OIII] emission around the nebula (Sankrit & Hester1997)
which is interpreted as a cooling region behind a radiative shock
propagating at
and X-ray emission
(Fesen et al.1997; Predehl & Schmitt1995). However, HST observations reveal a
thin shell of [OIII] emission around the nebula (Sankrit & Hester1997)
which is interpreted as a cooling region behind a radiative shock
propagating at ![]() km s
km s![]() in a medium of density
in a medium of density ![]() cm
cm![]() . Ironically, the Crab SNR may then no more be of the
``crab-type'' but may be re-classified as of the composite class (see
below).
. Ironically, the Crab SNR may then no more be of the
``crab-type'' but may be re-classified as of the composite class (see
below).
Such shells have also not been detected for other plerionic SNRs. If the tenuous environment in which these SNRs are expanding is the reason for non-detection of the shell in radio continuum emission, it has been suggested that one must look for signs of interaction with the surrounding atomic or molecular gas (Jones et al.1998). 21-cm neutral hydrogen observations of G074.9+1.2 (CTB87), which is a pulsar powered SNR with no outer shell, shows that this SNR lies within an expanding HI bubble (Wallace et al.1997). The radio continuum emission also shows signs of flattening at a point of apparent contact between the HI bubble and the SNR, lending further support to this model. However evidence for a shell of emission around other plerionic SNRs like 3C58 remains elusive.
Compact radio quiet thermal X-ray sources within SNRs have also been found in a few remnants (Gotthelf et al.1997; Vasisht & Gotthelf1997; Gotthelf & Vasisht1997). These compact objects may be radio quiet neutron stars in the SNRs and may thus explain the embarrassing lack of pulsar-SNR associations (Kaspi1998) in the sense that a non-pulsar neutron star or radio-quiet pulsar may be associated with many SNRs. The recent discovery of X-ray pulsations from some of these compact sources (Vasisht et al.2000; Gotthelf et al.2000) lend support to the idea that for these compact objects are indeed the elusive radio quiet neutron stars which are thought to be produced by the explosion and hence associated with the SNRs.
![\includegraphics[scale=0.5]{G0.9+0.1.PS}](img161.png)
|
This class of SNRs exhibit characteristics of both shell-type and
plerionic SNRs (Fig. 1.6). These SNRs are
characterized by flat spectrum emission from the central region with
a steeper spectrum shell of emission. Typical examples of this class
of SNRs are G000.9![]() 0.1, CTB80, G326.3
0.1, CTB80, G326.3![]() 1.8.
1.8.
With high resolution imaging now possible in the X-ray band, this class has grown to include what are referred to as ``centrally influenced'' remnants; e.g. objects with shock powered radio shells with centrally enhanced X-ray emission. The X-ray radiation can be in the form of hard X-ray non-thermal emission from a compact nebula and/or extended soft thermal X-ray emission. Rho & Petre (1998) term SNRs with thermal X-ray emission inside hollow radio shells as ``mixed morphology'' SNRs. The X-ray emission is proposed to come from the evaporation of clouds (of pre-explosion origin) by the reflected and reverse shocks. Many of the thermal X-ray composite SNRs are interacting with molecular clouds (conclusions drawn from molecular line and OH maser observations, e.g. W44, 3C391, W28, IC443) (Frail et al.1994; Frail & Mitchell1998; Claussen et al.1997; Yusef-Zadeh et al.1999) and it has been suggested that this may be a generic property of the class.
![\includegraphics[scale=0.5]{G3.7-0.2.LBAND.rot90.ps}](img162.png)
|
These remnants are characterized by a clear axis of symmetry with lower emission along the axis in between two brighter limbs (Kesteven & Caswell1987; Caswell et al.1989; Whiteoak & Gardner1968) (Fig. 1.7). Proposed explanations for such a morphology are either on the lines of ``extrinsic'' effects relating to the ambient ISM and magnetic field and ``intrinsic'' effects relating to the progenitor and its circumstellar medium. Such morphologies can be produced if the ejecta expands inside an elongated cavity (Bisnovatyi-Kogan et al.1990). Alternatively, ejecta expanding in a uniform magnetic field will preferentially compress where the shock normal is perpendicular to the field lines producing enhanced emission where the magnetic field is more compressed (van der Laan1962). On the other hand, such morphologies can be produced due to intrinsic reasons like toroidal distribution of ejecta (Bodenheimer & Woosley1983) or due to initial high velocity of the progenitor (Rozyczka et al.1993) or intrinsic preferentially polar outflows from the central compact object (Manchester & Durdin1983; Willingale et al.1996).
Analysis of highly resolved images of 17 barrel shaped SNRs done by Gaensler (1998) show evidence of a statistically significant tendency for the bilateral axes to be aligned with the Galactic plane. This is interpreted as lending support for the extrinsic effects being the dominant cause for the observed morphology - namely the alignment of the magnetic field with the Galactic plane.
![\includegraphics[scale=0.45]{long.hist.eps}](img163.png)
|
Fig. 1.8 shows the distribution of the known Galactic SNRs as a function of Galactic longitude. Most of the known Galactic SNRs are in the 1st or the 4th quadrant. This bias towards the inner Galaxy is attributed to the fact that most of the star forming regions are in the Galactic arms which cover a larger fraction of the inner Galaxy. However, there appears to be a mild lack of SNRs in the 4th quadrant compared to the 1st quadrant which is most likely to be due to some selection effect, probably due to the use of different telescopes in these quadrants (Gray1994b; Clark et al.1975b; Altenhoff et al.1979; Kesteven & Caswell1987; Duncan et al.1997b; Clark et al.1975a; Duncan et al.1997a; Whiteoak & Green1996; Gray1994a).
The incompleteness of the current Galactic SNR catalogue has been
pointed out by Green (1991). He noted that the catalogue
is incomplete in very large low surface brightness as well compact
small sized young SNRs. Low surface brightness SNRs may be missed due
to sensitivity limits of the observations. Higher frequency
observations may also miss them because they are also inherently
weaker at high frequencies. Such SNRs will also be missed in
interferometric observations which are not sensitive to emission at
angular scales larger than a maximum value. Small sized compact SNRs
may be missing because of confusion with compact source of thermal
emission. Any statistical result based on the current SNR catalogue
is therefore likely to be affected by these selection biases. This is
reflected in about a factor of ![]() error in the distance estimates
for SNRs using the statistically derived
error in the distance estimates
for SNRs using the statistically derived ![]() -
-![]() relation.
Green (1991) also argues that the proposed
relation.
Green (1991) also argues that the proposed ![]() -
-![]() -
-![]() relation is
not statistically significant.
relation is
not statistically significant.
Statistical studies of a complete sample of Galactic SNRs can help answer many question about the remnants themselves, their parent supernovae, their relation to pulsars and their interactions with the ISM and the ambient magnetic field. Observations to remove, if possible, the above mentioned biases in current catalogues are therefore important from the point of view of Galactic SNR research.
Most of the emission from SNRs is due to the interaction of the blast
wave with the material into which it expands (the circumstellar
envelope or the ISM). Low frequency spectral turnover, pulsar
dispersion measures, HI absorption and brightness variations across
SNRs, in particular along the shells of the shell-type SNRs suggest
that the environments into which SNR expand are non-uniform. This is,
however, hardly surprising since the structure and energetics of the
ISM is largely dominated by star forming regions and supernova
explosions, both of which are localized compared to the extent of the
Galaxy. These density variations in the ISM are in-turn also expected
to shape the morphologies of the SNRs. Interaction of the blast wave
with higher density regions will result in stronger deceleration
resulting in higher turbulence. This produces larger particle
acceleration and consequently stronger synchrotron emission in such
regions of interaction. On the other hand, the ejecta will expand at
a more rapid rate in a lower density region and may even become radio
loud at comparatively later times when the swept-up mass is enough to
decelerate the blast wave. These effects are believed to give rise to
the blow-out (G312.4![]() 0.4), one-sided (G338.1
0.4), one-sided (G338.1![]() 0.4) or irregular
morphologies. The expanding blast also interacts with the ambient
magnetic field and amplifies it via turbulent amplification or by
simple compression of the frozen-in fields. This interaction of the
blast wave with the magnetic field is believed to be responsible for
the barrel shaped SNRs and it has been suggested that many
intrinsically barrel shaped SNRs may not appear to be so due to
projection effects (Gaensler1998).
0.4) or irregular
morphologies. The expanding blast also interacts with the ambient
magnetic field and amplifies it via turbulent amplification or by
simple compression of the frozen-in fields. This interaction of the
blast wave with the magnetic field is believed to be responsible for
the barrel shaped SNRs and it has been suggested that many
intrinsically barrel shaped SNRs may not appear to be so due to
projection effects (Gaensler1998).
Spatially resolved spectral index variations across SNRs trace changes in particle kinetic energies or magnetic field strengths or both. Both of these could also be due to the inhomogeneous nature of the medium into which the ejecta expands; reliable spatially resolved spectral index maps of SNRs thus give a handle on the scale of inhomogeneities in the ISM (Anderson & Rudnick1993; Katz-Stone et al.2000a). Spectral index changes across SNRs probe scales smaller than the size of the remnants. If the intrinsic properties of the SNRs can be independently established, spectral index changes between widely separated SNRs will probe scales of the order of the separation between the remnants.
It has been shown recently that the OH (1720 MHz) emission is associated
with SNRs while the other OH maser transitions are associated with HII
regions (Frail & Mitchell1998). Both theoretical and
observational evidence
(Reach & Rho1998; Reach & Rho1999; Frail & Mitchell1998) suggests
that the OH (1720 MHz) masers are associated with the C-type shocks and
are collisionally pumped in molecular clouds at temperatures and
densities of ![]() K and
K and ![]() cm
cm![]() respectively
(Lockett et al.1999, and references therein). OH masers at 1665, 1667
and 1612 MHz cannot be produced under these physical conditions and
the absence of these lines along with the detection of OH (1720 MHz) emission favors this interpretation. The measurements of the post
shock density and temperature for IC443 (van Dishoeck et al.1993), W28,
W44 and 3C391 (Frail & Mitchell1998) are in excellent agreement
with these theoretical predictions. A solution to the problem of
producing OH, which is not directly formed by shocks, are proposed by
Wardle et al. (1999). They suggest that the molecular cloud is
irradiated by the X-rays produced by the hot gas in the interior of
the SNR. This leads to photo-dissociation of the H
respectively
(Lockett et al.1999, and references therein). OH masers at 1665, 1667
and 1612 MHz cannot be produced under these physical conditions and
the absence of these lines along with the detection of OH (1720 MHz) emission favors this interpretation. The measurements of the post
shock density and temperature for IC443 (van Dishoeck et al.1993), W28,
W44 and 3C391 (Frail & Mitchell1998) are in excellent agreement
with these theoretical predictions. A solution to the problem of
producing OH, which is not directly formed by shocks, are proposed by
Wardle et al. (1999). They suggest that the molecular cloud is
irradiated by the X-rays produced by the hot gas in the interior of
the SNR. This leads to photo-dissociation of the H![]() O molecules,
which is produced by the shock wave in copious amounts, behind the
C-type shock resulting in the required enhancement of OH just behind
the shock. Indeed, such maser emission has been found in SNRs whose
morphologies have long been suspected to be shaped by their
interaction with nearby molecular clouds
(Green et al.1997; Frail et al.1994; Claussen et al.1997). The fact
that OH (1720 MHz) emission is possible for a very narrow range of
physical parameters of the gas and other OH transitions in this range
do not produce maser emission provides a powerful tool to probe the
interaction of SNRs with molecular clouds. Detection of extended
OH (1720 MHz) emission along with compact maser spots, tracing the radio
continuum emission is suggestive of the maser emission tracing the
extended region of such an interaction (Yusef-Zadeh et al.1999).
O molecules,
which is produced by the shock wave in copious amounts, behind the
C-type shock resulting in the required enhancement of OH just behind
the shock. Indeed, such maser emission has been found in SNRs whose
morphologies have long been suspected to be shaped by their
interaction with nearby molecular clouds
(Green et al.1997; Frail et al.1994; Claussen et al.1997). The fact
that OH (1720 MHz) emission is possible for a very narrow range of
physical parameters of the gas and other OH transitions in this range
do not produce maser emission provides a powerful tool to probe the
interaction of SNRs with molecular clouds. Detection of extended
OH (1720 MHz) emission along with compact maser spots, tracing the radio
continuum emission is suggestive of the maser emission tracing the
extended region of such an interaction (Yusef-Zadeh et al.1999).
As mentioned above, radio emission from SNRs is synchrotron radiation
which has a non-thermal power law dependence on frequency with a
negative spectral index ![]() (
(
![]() ). This makes
the emission progressively stronger at lower frequencies (see
Section 1.1). Thermal emission from typical HII
regions, on the other hand has a flat spectrum above
). This makes
the emission progressively stronger at lower frequencies (see
Section 1.1). Thermal emission from typical HII
regions, on the other hand has a flat spectrum above ![]() GHz.
Below this frequency the optical depth is much greater than 1 and the
spectrum turns over with a spectral index of 2. Continuum spectra of
Galactic objects at low frequencies are therefore frequently used to
distinguish between thermal and non-thermal sources of emission
(Kassim & Weiler1990; Kassim et al.1989a; Subrahmanyan & Goss1995).
Radio emission from SNRs is typically also extended, often with low
surface brightness, with most of the remnants exhibiting easily
identifiable morphologies. Detection of extended non-thermal emission
in the Galaxy, with no thermal emission, has been the criterion used to
identify Galactic sources as SNRs. Low frequency observations of SNRs
also provide an added advantage in the sense that the surface
brightness of typical SNRs increases at low frequencies, making it
easier to detect and map them for detailed studies.
GHz.
Below this frequency the optical depth is much greater than 1 and the
spectrum turns over with a spectral index of 2. Continuum spectra of
Galactic objects at low frequencies are therefore frequently used to
distinguish between thermal and non-thermal sources of emission
(Kassim & Weiler1990; Kassim et al.1989a; Subrahmanyan & Goss1995).
Radio emission from SNRs is typically also extended, often with low
surface brightness, with most of the remnants exhibiting easily
identifiable morphologies. Detection of extended non-thermal emission
in the Galaxy, with no thermal emission, has been the criterion used to
identify Galactic sources as SNRs. Low frequency observations of SNRs
also provide an added advantage in the sense that the surface
brightness of typical SNRs increases at low frequencies, making it
easier to detect and map them for detailed studies.
Interferometric telescopes are however insensitive to scales larger than those corresponding to the smallest projected baseline. Single dish telescopes, on the other hand, are sensitive to emission at all scales in the field. However, they provide the sensitivity and required resolution only at high frequencies. Many observations of SNRs till recently were therefore done using single dish instruments at high frequencies. However, apart from the contaminating thermal emission at these frequencies as well as inherently lower emission from SNRs, such observations are more prone to large scale confusing emission, which is abundantly present in the Galactic plane. The resolution of low frequency single dish observations is also not enough to resolve the extended emission.
Although high resolution interferometric observations of Galactic SNRs
have been carried out, imaging at low frequencies using
interferometers is also relatively tougher due to the problems arising
from higher level of radio frequency interference (RFI), higher phase
noise at low frequencies (due to various reasons ranging from cross
talk to ionospheric phase corruption), non-co-planarity of arrays
requiring much more complex software and higher computing power, etc.
Hence, even interferometric observations have been typically done at
frequencies ![]() GHz.
GHz.
Sensitive low frequency observations which are also sensitive to extended emission are therefore most appropriate for SNR research. Aperture synthesis telescopes like the GMRT operating at relatively low frequencies are well suited for such observations.
Low frequency aperture synthesis telescopes like the GMRT offer several unique advantages from the point of view of SNR research. The GMRT is best suited for SNR observations owing to its sensitivity, relatively high resolution as well as sensitivity to large scale emission at low frequencies. Observations done for this dissertation extensively used the GMRT which has only recently come to a stage where enough antennas are available in the interferometric mode to attempt the imaging of extended sources. Interferometry at low frequencies, however, poses new challenges in data calibration and analysis, which are interesting in their own right. A substantial fraction of the work done for this dissertation involved the debugging and calibration of the telescope, to enable the observations discussed above to be carried out. Further, large amounts of software were required to be written, both to carry out debugging activity as well as to enable flagging and calibration of telescope data in a semi-automated fashion. The origin of the problems in low frequency interferometry and the required on-line data monitoring and off-line data analysis are briefly described below.
The plasma frequency of the ionosphere is ![]() MHz. The only
cosmic radio emission reaching the surface of the earth is at
frequency significantly higher than this value. However radio
observations at a few 100 MHz are still severely affected by the
ionosphere. The ionosphere is modeled as a thin (compared to the
distance from the observing plane) slab of inhomogeneous plasma. A
plane wave incident on the ionosphere filled with plasma blobs will
emerge with the plasma fluctuations imprinted on the phase of the
wavefront (Fig.1.9). The amplitude of this wave front
will remain largely unchanged but the phase is no longer constant.
The RMS phase fluctuations of the visibility phase induced due to the
Earth's ionosphere can be written as (Cronyn1972; Thompson et al.1986, and references
therein)
MHz. The only
cosmic radio emission reaching the surface of the earth is at
frequency significantly higher than this value. However radio
observations at a few 100 MHz are still severely affected by the
ionosphere. The ionosphere is modeled as a thin (compared to the
distance from the observing plane) slab of inhomogeneous plasma. A
plane wave incident on the ionosphere filled with plasma blobs will
emerge with the plasma fluctuations imprinted on the phase of the
wavefront (Fig.1.9). The amplitude of this wave front
will remain largely unchanged but the phase is no longer constant.
The RMS phase fluctuations of the visibility phase induced due to the
Earth's ionosphere can be written as (Cronyn1972; Thompson et al.1986, and references
therein)
![\includegraphics[scale=0.8]{ionosphere.ps}](img173.png)
|
| (4.20) |
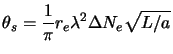 |
(4.21) |
| (4.22) |
| (4.23) |
The result of the these fluctuations is that a point source is broadened into a gaussian of diameter given by
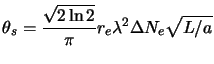 |
(4.24) |
Ionospheric electron density also changes as a function of time due to diurnal and seasonal changes in the position of the Sun and also due to the activity on the Sun. Since the induced phase fluctuations scale with the wavelength, the effect of ionosphere is more severe at low frequencies. These phase errors need to be calibrated before the measured visibilities can be used for mapping. Long term (several tens of minutes) variations in the phase of an interferometer can be measured by periodic observation of a source of known structure, usually referred to as the phase calibrator, using the self-cal algorithm which decomposes the visibility phases into antenna based phases (Cornwell & Wilkinson1981; Pearson & Readhead1984; Thompson & D'Addario1982). However for this, it is assumed that the variations in phase are small at angular scales smaller than the size of the primary beam of the antennas (iso-planatic case). At low frequencies, this assumption can break, at least for some fraction of time, and the derived phase corrections will not correct for the phase noise completely over the whole field. Schwab (1984) and Subrahmanya (1989) have described methods to relax the iso-planatic assumption. However, such algorithms have never been tried in real life or demonstrated to work well. This remains a potential problem, at least for high dynamic range imaging at low frequencies.
The calibrated visibility function measured by an aperture synthesis telescope is given by4.2
For a small field of view (
![]() ),
), ![]() is related to the
image by a 2D Fourier transform. However for
is related to the
image by a 2D Fourier transform. However for
![]() where
where
![]() and
and
![]() are the widths of the primary beam and the telescope
resolution element, the image plane can no longer be expressed as a 2D
Fourier transform of the visibility function (Cornwell & Perley1999).
The sky can no longer be approximated by a 2D plane and must be
modeled as the surface of a sphere, referred to as the Celestial
sphere. To continue to approximate Equation 1.25 as a 2D
Fourier transform relation between the sky brightness distribution and
the visibility will introduce severe distortions in the image away
from the phase centre. The longest baseline for the GMRT at 327 MHz is
are the widths of the primary beam and the telescope
resolution element, the image plane can no longer be expressed as a 2D
Fourier transform of the visibility function (Cornwell & Perley1999).
The sky can no longer be approximated by a 2D plane and must be
modeled as the surface of a sphere, referred to as the Celestial
sphere. To continue to approximate Equation 1.25 as a 2D
Fourier transform relation between the sky brightness distribution and
the visibility will introduce severe distortions in the image away
from the phase centre. The longest baseline for the GMRT at 327 MHz is
![]() km. Imaging with the GMRT at 327 MHz using baselines longer
than
km. Imaging with the GMRT at 327 MHz using baselines longer
than ![]() km crosses the limit where the sky can be
approximated, and a full 3D treatment of the problem is required to
make distortion free images.
km crosses the limit where the sky can be
approximated, and a full 3D treatment of the problem is required to
make distortion free images.
This problem can be handled by treating
![]() as an
independent co-ordinate. Re-writing Equation 1.25 as
as an
independent co-ordinate. Re-writing Equation 1.25 as
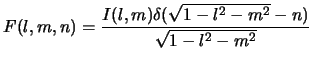 |
(4.27) |
The Galactic plane at low frequencies exhibits complex emission all over the field of view. Hence, even if the source of interest is compact and close to the pointing centre, 2D imaging cannot be applied since the distortions of sources away from the pointing centre (which is assumed to be also the phase centre) will have unacceptable effects all over the image. It is therefore necessary to map the full field of view, even if the size of the source of interest is small compared to the primary beam. Polyhedron imaging is implemented in the Astronomical Image Processing System (AIPS) package and was extensively used for making full primary beam images this dissertation.
In these early days of the GMRT, apart from other sources of data corruption like radio frequency interference (RFI), ionospheric scintillation, etc., data was frequently corrupted due to the failure of various systems. Monitoring the data quality and the health of the system during the observations was therefore of paramount importance. Since there were many sources of data corruption and the manner in which they affected the data were varied, it is useful to develop techniques and software which can automatically identify as many of these problems as early on in the data analysis process as possible. Identifying sources of data corruption, general debugging of the instrument, etc. however require sophisticated and efficient software for data analysis, browsing, and display. Extensive software was developed for this purpose in the form of general purpose object oriented libraries as well as programs for on-line and off-line data processing and display.
The effort invested in software development is optimally used if the resultant software is easy to use at the user level and easy to extend at the programmer level. This is also almost necessary for software which is expected to be used by a relatively larger number of users. Development of a user interface which is easy to use as well designing the entire software such that it is easy to extend is therefore important. Also, a user interface which is not consistent with the functionality of the application programs to which it interfaces is unlikely to be useful. It is therefore desirable to develop a user interface which, as far as possible, automatically evolves with the application programs. The modern Object Oriented software design philosophy was adopted to achieve exactly this goal. Software designed in an Object oriented manner is highly modular and the modules are loosely coupled. The software is designed as set of ``objects'' which map closely to real-life objects in the problem being solved. Usually, these real-life objects do not change significantly over the software life time, but the coupling between various objects can drastically change. Such changes can be very easily incorporated in a big software system designed as set of objects. Apart from ease of maintenance, this also produces reliable software which is easy to debug.
A user interface, which becomes part of the compiled application programs (as against a user interface as an independent entity which loads and runs the applications programs) was developed in the form of a set of libraries. Such a user interface is referred to as an embedded user interface. Libraries which provide a high level, astronomically useful interface for manipulating the GMRT visibility database were also developed. Using these libraries, programs for data editing, semi-automatic data flagging, on-line monitoring of the data, computation for antenna-based complex gains, amplitude and phase calibration, etc. were also developed.
The visibility function ![]() , depends on a number of telescope
parameters like the system temperature (
, depends on a number of telescope
parameters like the system temperature (![]() ), antenna
sensitivity, antenna fixed delays, antenna positions, etc. For
debugging as well as for on-line data monitoring, it was frequently
required to extract this data in various representations (e.g.,
Cartesian versus polar representation of complex numbers). Since the
complex visibilities are a function of a multitude of parameters, and
different debugging purposes require viewing
), antenna
sensitivity, antenna fixed delays, antenna positions, etc. For
debugging as well as for on-line data monitoring, it was frequently
required to extract this data in various representations (e.g.,
Cartesian versus polar representation of complex numbers). Since the
complex visibilities are a function of a multitude of parameters, and
different debugging purposes require viewing ![]() with respect to
various quantities, it was necessary to develop a compact macro
language parser to extract and display the data in a flexible and
programmable manner. This macro language was implemented in the form
of stand alone libraries as well as an application program which was
extensively used for this dissertation.
with respect to
various quantities, it was necessary to develop a compact macro
language parser to extract and display the data in a flexible and
programmable manner. This macro language was implemented in the form
of stand alone libraries as well as an application program which was
extensively used for this dissertation.
The self-cal algorithm can be used to compute antenna based complex gains from the complex visibilities for a source of known structure. However, it is very sensitive to the presence of data from malfunctioning antennas or from a malfunctioning correlator. During the course of the observations, it was frequently the case that the data from a few antennas was unusable, at least for some fraction of the observing time. A large fraction of diagnosis of problems in the data/telescope is often done by examining the antenna based complex gains, which are computed using the self-cal algorithm which in turn required careful flagging of malfunctioning antennas/baselines. An algorithm was therefore implemented which was robust in such conditions and could identify bad baselines/antennas automatically. This was done by (1) automatically eliminating out-lying points, (2) doing two passes to eliminate dead/bad antennas. This algorithm was also used to identify and flag corrupted data in a semi-automatic fashion.
Signals from the two orthogonally polarized feeds are brought to the base of the antenna via co-axial cables, which run physically close to each other. These signals are then brought to the a central location via optical fibers where they are converted to baseband signals. The two orthogonally polarized signals can leak in each other at various points in the signal path resulting into polarization impurity. To minimize this leakage, the technique of Walsh switching (Thompson et al.1986, and references therein) is used wherein the two signals are multiplied by two orthogonal trains of square waves, called the Walsh functions. Later, before correlating the signals from different antennas, these Walsh switched signals are multiplied by the inverse Walsh functions to recover the original signals. Any leaked signal from one polarization channel to the other at time scales longer than the period of the Walsh functions then averages to zero.
The planned Walsh switching has not yet been implemented for the GMRT. In any case, polarization impurity introduced before the switching point will not be removed by Walsh switching. This leakage is a significant source of noise at 150 MHz and also contributes noise at all other bands, albeit at a lower level and manifests itself in the form of increased closure errors in the system (Rogers1983). The current GMRT correlator computes only the co-polar visibilities (i.e. RR and LL visibilities only). Even with the planned extension of the correlator where the cross-polar visibilities (i.e. RL and LR visibilities) will also be computed, one can think of observations which will be done using the higher frequency resolution provided by the GMRT correlator in the non-polar mode. All such data will then be affected by errors related to this polarization impurity related errors. Rogers (1983) pointed out in the context of the VLBA, that polarization leakage causes closure errors even in nominally co-polar visibilities. Massi et al. (1997) have carried out a detailed study of this effect for the telescopes of the European VLBI Network (EVN). The polarization leakage in some of the EVN antennas corrupts the co-polar visibilities at a level visible as a reduction in the dynamic range of the maps (Massi & Aaron1997a; Massi & Aaron1997b; Massi et al.1998).
Non-polarimetric observations for imaging constitute a large fraction of observations done using interferometers where only the co-polar visibilities are recorded. The calibrators used for such observations are usually unpolarized. Since the above mentioned closure errors will affect such data adversely, a method to measure the polarization leakage using only the co-polar visibilites from an unpolarized calibrator to correct for these closure errors will be of use, particularly for high dynamic range imaging.
Low frequency continuum spectra, radio morphology and, if possible
polarization measurements are the key observables used to identify
SNRs in the Galaxy. Spectra at frequencies greater than ![]() GHz
suffer from contaminating thermal emission. Therefore, although
higher angular resolution observations can be done at high
frequencies, low frequency radio observations are more suited for SNR
research. However with the lower resolutions and sensitivities at low
frequencies, identification of the morphology, particularly in regions
with complicated emission becomes difficult. High resolution
sensitive observations at low radio frequencies therefore appears to
be the optimal observation expected to yield rich dividends for
various aspects of SNR research. This thesis reports the work done on
these lines using the GMRT.
GHz
suffer from contaminating thermal emission. Therefore, although
higher angular resolution observations can be done at high
frequencies, low frequency radio observations are more suited for SNR
research. However with the lower resolutions and sensitivities at low
frequencies, identification of the morphology, particularly in regions
with complicated emission becomes difficult. High resolution
sensitive observations at low radio frequencies therefore appears to
be the optimal observation expected to yield rich dividends for
various aspects of SNR research. This thesis reports the work done on
these lines using the GMRT.
The main thrust of the thesis is the study of Galactic SNRs taking advantage of the high sensitivity and resolution of the GMRT which has recently become available for scientific usage. Since this work was done in the early stages of the GMRT, a large fraction of time was also spent in debugging the instrument and in developing extensive software for data browsing, display and off-line analysis. New algorithms and techniques were also developed which were useful, in particular for the GMRT, and, in general, for low frequency interferometry.
While debugging the GMRT, need for a sophisticated software for data
browsing, display and analysis was felt early on. As a result, large
amounts of software (![]() lines of code in C++, C and FORTRAN) was written with the goal of keeping it efficient and yet
simple so that the turn around time between observations and results
from data analysis is minimized. This software was also written in a
modern object oriented fashion, with the hope that many more
astronomers/engineers will find it useful to write useful application
programs using the the underlying software libraries as well as to
extend the software system.
lines of code in C++, C and FORTRAN) was written with the goal of keeping it efficient and yet
simple so that the turn around time between observations and results
from data analysis is minimized. This software was also written in a
modern object oriented fashion, with the hope that many more
astronomers/engineers will find it useful to write useful application
programs using the the underlying software libraries as well as to
extend the software system.
The thesis is organized in the form of eight chapters and four
appendices. The present chapter briefly describes the model for
supernova explosions and introduces the theoretical concepts of radio
synchrotron emission in Section 1.1. Particular
emphasis is laid on the fact that low radio frequency observations for
the purpose of identification of SNRs in the Galaxy provides a crucial
advantage over high frequency observations. The various stages of the
evolution of SNRs are described in Section 1.2.
Proposed mechanisms to explain the observed non-thermal emission from
SNRs are discussed in Section 1.2.1 and the
information drawn from measured continuum spectra of SNRs is discussed
in Section 1.2.2. At frequencies higher than ![]() GHz, thermal emission from HII regions in the Galaxy is strong and
sometimes even dominant. The spectral signatures and nature of
thermal emission in the presence of absorbing foreground medium are
discussed in Section 1.2.3. Various observed radio
morphologies, distribution of SNRs in the Galaxy and the effects of
the ISM on the observed properties of SNRs are discussed in
Sections 1.2.4, 1.2.5 and
1.3 respectively.
GHz, thermal emission from HII regions in the Galaxy is strong and
sometimes even dominant. The spectral signatures and nature of
thermal emission in the presence of absorbing foreground medium are
discussed in Section 1.2.3. Various observed radio
morphologies, distribution of SNRs in the Galaxy and the effects of
the ISM on the observed properties of SNRs are discussed in
Sections 1.2.4, 1.2.5 and
1.3 respectively.
Chapter 2 describes the GMRT from an astronomical point of view. The underlying principle of aperture synthesis is discussed in Section 2.1, with emphasis on the problems related to imaging at low frequencies. Section 2.2 briefly describes the parabolic dishes and the geometry of the array. Section 2.3 describes the signal path from the antennas feeds till the digital back-end correlator while Section 2.4 describes the astronomically relevant parameters of the telescope. Most of the observations included in this dissertation were done when the GMRT hardware as well software was in a state of being debugged. Consequently, a large fraction of the time was spent in debugging activities, which required understanding the details of the hardware - particularly of the GMRT FX-type correlator. The GMRT correlator hardware and associated software is described in some detail in Section 2.5. Section 2.5.1 describes the algorithm used for accurate time stamping of the data in the data acquisition software. Precise location of the antennas on the ground as well as the fixed instrumental delay suffered by the signal from individual antennas before reaching the correlator are two important parameters of an aperture synthesis telescope. Before imaging could be attempted, these measurements were made for the GMRT. Details of the baseline and antenna fixed delay calibration and its results are described in Section 2.6.
Chapter 3 very briefly describes the design and implementation of the GMRT off-line data analysis software system, which was extensively used during the course of this work. Section 3.1 discusses the need for the development of such a software system. Section 3.2 describes the philosophy behind the design of this software system consisting of a set of generic libraries and a number of application programs. Data manipulation libraries are described briefly in Section 3.3 while the user interface system and a few selected application programs, most extensively used during the course of this work, are described in Sections 3.4 and 3.5 respectively.
Chapter 4 describes the 325-MHz GMRT observations of
a sample of candidate SNR fields. Section 4.1
describes the parameters of these observations. Mapping in the
Galactic plane at 325-MHz with the GMRT requires mapping of the entire
field of view which in turn requires use of specialized imaging and
deconvolution algorithms. Section 4.2 discusses
the techniques used from imaging at low frequencies, which were used
for mapping the GMRT data. Section 4.3 describes the
observational procedure used for these observations including the use
of off-line data analysis software for on-line monitoring of the
system health and the data quality. The details of data analysis and
calibration are described in Section 4.4.
Section 4.5 discusses the details related to inversion of the
visibility data and deconvolution of the images. Finally,
Section 4.6 presents the full primary beam 325-MHz images of
all the fields. Most of the SNRs studied in this dissertation are
large in angular size (typically ![]() arcmin). Although these GMRT
observations could provide typical resolution of
arcmin). Although these GMRT
observations could provide typical resolution of ![]() arcsec for
these southern fields, the maps presented here are typically at arcmin
resolution. The reason for this is two fold: (1) since many of the
SNRs had low surface brightness, lower resolution maps show the
morphology more clearly (2) large scale emission tend to ``break-up''
at the highest resolution due to a combination of problems of
deconvolution of large sources as well as phase noise that could not
be calibrated. For a few fields, where the angular size of the
sources of interest was of the order of arcmin, high resolution images
were used.
arcsec for
these southern fields, the maps presented here are typically at arcmin
resolution. The reason for this is two fold: (1) since many of the
SNRs had low surface brightness, lower resolution maps show the
morphology more clearly (2) large scale emission tend to ``break-up''
at the highest resolution due to a combination of problems of
deconvolution of large sources as well as phase noise that could not
be calibrated. For a few fields, where the angular size of the
sources of interest was of the order of arcmin, high resolution images
were used.
Full primary beam maps of almost all the fields at 325-MHz exhibit a number of sources of compact as well extended emission, particularly in the Galactic plane. The primary goal of these observations was the low frequency study of Galactic SNRs in the fields - many of which were not confirmed SNRs. Chapter 5 goes on to discuss the SNRs in these fields. Section 5.1 discusses the difference between low and high frequency observations of Galactic SNRs to bring forth the advantages offered by deep high resolution observations at low frequency. Section 5.2 then discusses the individual candidate SNRs in the fields. Some of the fields also contained other previously identified SNRs. For a few of them, these 325-MHz observations are the first observations at this frequency; in fact, these are also the first high resolution observations at this frequency for all these sources. These results are described and discussed in Section 5.3. Finally, Section 5.4 discusses these results in a broader perspective of Galactic SNR research.
Other sources in the field are discussed in Chapter 6. Section 6.1 briefly discusses the nature of other dominant sources of radio emission and Section 6.2 presents a list of point sources in the fields along with their measured flux densities at 325-MHz and, where possible, at 1400 MHz. Section 6.3 discusses the sources of extended emission in these fields, which are not SNRs. These high resolution observations at relatively low frequency are the first ever observations of these objects and the somewhat unexpected significant extended emission seen at this frequency is interesting from the point of view of better understanding of these sources (usually classified as ``thermal''). Section 6.5 concludes the chapter with a summary of the results from these observations.
A technique for the computation of polarization leakage using only the co-polar visibilities is described in Chapter 7. Section 7.2 describes the motivation which led to the development of this technique. Section 7.3 mathematically describes the algorithm and also presents the results of the simulations done to test it. Section 7.4 presents the results of the tests done with real data acquired in a controlled experiment and the interpretation of the results in terms of the magnitude of the polarization leakage for various antennas. The Poincaré sphere is a convenient and possibly more intuitive representation of the polarization state of radiation. Interpretation of these results on the Poincaré sphere and the equivalence of the polarization leakage induced phase closure errors and the Pancharatanam phase is discussed in Section 7.5. Since only co-polar visibilities are used for the computation of polarization leakage, the solutions are not unique, but still provide useful information about the polarization properties of the antennas. This is discussed in Section 7.6.
Chapter 8 gives consolidated conclusions and results from this work. Section 8.1 describes the major results from the testing and debugging of the GMRT and the software developed for the purpose. Section 8.2 discusses the astronomical results from the observations of the candidate SNRs done for this dissertation. Section 8.3 discusses the inferences about other sources in the fields based on these low frequency observations. Section 8.4 proposes the future directions of research in the fields of Galactic SNRs, compact/Ultra compact H II regions as well as in the field of developing data analysis techniques for radio interferometry at low frequencies and related software development.
Details of the user interface for the off-line software is included as Appendix A. A flexible mechanism was developed to allow easy extraction for any type of data from the GMRT visibility database. This was implemented in the form of a macro language; and the parser and complier for this language is implemented as a stand alone library and used in the program xtract. Details of all this work are included as Appendix B. A flexible antenna and baseline naming convention is uniformly used in all off-line application programs. This convention is described in Appendix C. Finally, Appendix D presents the formulation of the problem of computation of antenna based complex gains from the measured complex visibilities. The iterative equations are derived using complex calculus and the interpretation of these equations for better understanding of the algorithm is also presented.