


Next: Bibliography
Up: Computation of antenna based
Previous: Estimation of the system
Contents
Derivation of  using real and imaginary parts
using real and imaginary parts
 s are complex functions. One can therefore write
s are complex functions. One can therefore write  in terms of
in terms of
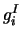 and
and
 , the real and imaginary parts of
, the real and imaginary parts of  and minimize
with respect to
and minimize
with respect to 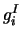 and
and
 separately. It is shown here that
the complex arithmetic achieves exactly this and the results are same
as that given by complex calculus. The superscripts
separately. It is shown here that
the complex arithmetic achieves exactly this and the results are same
as that given by complex calculus. The superscripts  and
and  in
the following are used to represent the real and imaginary parts of
complex quantities.
in
the following are used to represent the real and imaginary parts of
complex quantities.
Expanding Equation D.5, ignoring 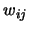 s and writing it
in terms of real and imaginary parts we get
s and writing it
in terms of real and imaginary parts we get
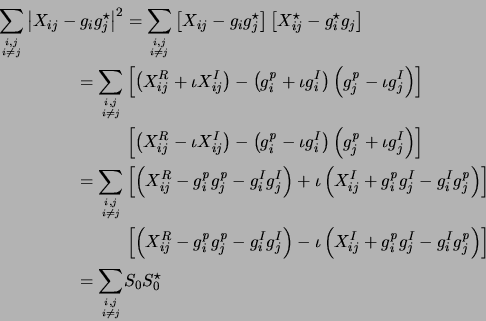 |
(15.14) |
where
![$\displaystyle S_0=\left[X_{ij}^R- {g_i^{\it p}}{g_j^{\it p}}- g_i^Ig_j^I\right]...
...iota \left[X_{ij}^I+ {g_i^{\it p}}g_j^I- g_i^I{g_j^{\it p}}\right] %%Imag part
$](img1172.png) |
(15.15) |
Taking partial derivative of  with respect to
with respect to
 and
reintroducing
and
reintroducing 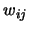 , we get
, we get
![\begin{displaymath}\begin{split}{\partial S \over \partial {g_i^{\it p}}}=&\sum\...
...I}^2 - {g_i^{\it p}} {{g_j^{\it p}}}^2\right]w_{ij} \end{split}\end{displaymath}](img1173.png) |
(15.16) |
Therefore,
![$\displaystyle {\partial S \over \partial {g_i^{\it p}}}= -2\sum\limits_{j \atop...
...t[Re(X_{ij}g_j^\star ) - \left\vert g_j\right\vert^2 {g_i^{\it p}}\right]w_{ij}$](img1174.png) |
(15.17) |
Equating
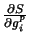 to zero, we get
to zero, we get
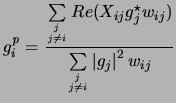 |
(15.18) |
Similarly
![$\displaystyle {\partial S \over \partial g_i^I}=-2\sum\limits_{j \atop {j \ne i}}\left[Im(X_{ij}g_j^\star) - \left\vert g_j\right\vert^2 g_i^I\right] w_{ij}$](img1177.png) |
(15.19) |
Therefore the equivalent imaginary part of Equation D.18
is
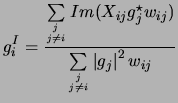 |
(15.20) |
writing
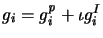 and substituting for
and substituting for
 and
and 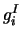 from Equation D.18 and D.20 respectively, we
get
from Equation D.18 and D.20 respectively, we
get
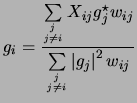 |
(15.21) |
This is same as Equation D.8, which was arrived at by
evaluating a complex derivative of Equation D.5 as
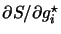 , treating
, treating  and
and 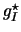 as
independent variables. Evaluating
as
independent variables. Evaluating
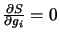 would give the complex conjugate of Equation D.21.
Hence,
would give the complex conjugate of Equation D.21.
Hence,
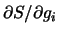 gives no independent information not
present in
gives no independent information not
present in
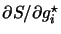 .
.



Next: Bibliography
Up: Computation of antenna based
Previous: Estimation of the system
Contents
Sanjay Bhatnagar
2005-07-07
![]() s and writing it
in terms of real and imaginary parts we get
s and writing it
in terms of real and imaginary parts we get
![$\displaystyle {\partial S \over \partial g_i^I}=-2\sum\limits_{j \atop {j \ne i}}\left[Im(X_{ij}g_j^\star) - \left\vert g_j\right\vert^2 g_i^I\right] w_{ij}$](img1177.png)