Estimation of the system temperature (
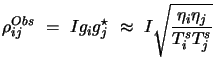 |
(15.11) |
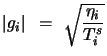 |
(15.12) |
All contributions to
![]() , which cannot be factored into
antenna dependent gains, will result in the reduction of
, which cannot be factored into
antenna dependent gains, will result in the reduction of
![]() .
. ![]() remaining constant, this will be
indistinguishable from an increase in the effective system
temperature. Since majority of later processing of interferometry
data for mapping (primary calibration, bandpass calibration, SelfCal,
etc.) is done by treating the visibility as a product of two antenna
based numbers, this is the effective system temperature which will
determine the noise in the final map (though, as a final step in the
mapping process, baseline based calibration can possibly improve the
noise in the map).
remaining constant, this will be
indistinguishable from an increase in the effective system
temperature. Since majority of later processing of interferometry
data for mapping (primary calibration, bandpass calibration, SelfCal,
etc.) is done by treating the visibility as a product of two antenna
based numbers, this is the effective system temperature which will
determine the noise in the final map (though, as a final step in the
mapping process, baseline based calibration can possibly improve the
noise in the map).
In the normal case of no significant baseline based terms
(
![]() ) in
) in ![]() , the system temperature as measured by
the above method will be equivalent to any other determination of
, the system temperature as measured by
the above method will be equivalent to any other determination of
![]() .
.
![]() can also be determined by recording interferometric data for a
strong point source with and without an independent noise source of
known temperature at each antenna. In this case
can also be determined by recording interferometric data for a
strong point source with and without an independent noise source of
known temperature at each antenna. In this case
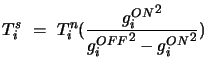 |
(15.13) |