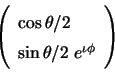 . Clearly,
. Clearly,
In this section we use right- and left-circular polarization states as
the basis. A general elliptically polarized state can be written as a
superposition of two states represented by the vector
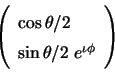 . Clearly,
. Clearly,
![]() corresponds to linear
polarization and
corresponds to linear
polarization and
![]() to elliptical polarization (see
Fig. 7.4). Increasing
to elliptical polarization (see
Fig. 7.4). Increasing ![]() by
by ![]() rotates
the direction of the linear state or the major axis of the ellipse by
rotates
the direction of the linear state or the major axis of the ellipse by
![]() . We can chose the phase of the basis so that
. We can chose the phase of the basis so that ![]() corresponding to linear polarization along the x-axis. The Poincaré
sphere representation of the state of polarization maps the general
elliptic state to the point (
corresponding to linear polarization along the x-axis. The Poincaré
sphere representation of the state of polarization maps the general
elliptic state to the point (
![]() ) on the sphere. The properties of this representation are
reviewed by Ramachandran & Ramaseshan (1961). We are concerned here
with one remarkable property, discovered by
Pancharatnam (1956); Pancharatnam (1975). Whenever there is
constructive interference between two sources of radiation, it is
natural to regard them as in phase. A remarkable property of this
simple definition manifests itself when we consider 3 sources of
radiation of different polarization - that if a source A is in phase
with B and B in phase with C, C in general need not be in phase with
A. The phase difference between A and C is known in the optics
literature as the geometric or Pancharatanam phase (see also
Ramaseshan & Nityananda (1986); Berry (1987)). We show that this naturally
occurs in radio interferometry of an unpolarized source with three
antennas of different polarizations.
) on the sphere. The properties of this representation are
reviewed by Ramachandran & Ramaseshan (1961). We are concerned here
with one remarkable property, discovered by
Pancharatnam (1956); Pancharatnam (1975). Whenever there is
constructive interference between two sources of radiation, it is
natural to regard them as in phase. A remarkable property of this
simple definition manifests itself when we consider 3 sources of
radiation of different polarization - that if a source A is in phase
with B and B in phase with C, C in general need not be in phase with
A. The phase difference between A and C is known in the optics
literature as the geometric or Pancharatanam phase (see also
Ramaseshan & Nityananda (1986); Berry (1987)). We show that this naturally
occurs in radio interferometry of an unpolarized source with three
antennas of different polarizations.
![\includegraphics[]{Images/poincare_sphere.ps}](img1085.png)
|
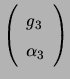
Let the polarization states of the three antennas be represented by
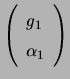 ,
,
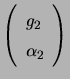 , and
, and
 in a
circular basis. Denoting the vector
in a
circular basis. Denoting the vector
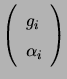 by
by ![]() , one clearly see that the
visibility on the 1-2 baseline is proportional to
, one clearly see that the
visibility on the 1-2 baseline is proportional to
![]() . Hence the closure phase around a triangle made by antennas
1, 2, and 3 is the phase of the complex number (also called the triple
product)
. Hence the closure phase around a triangle made by antennas
1, 2, and 3 is the phase of the complex number (also called the triple
product)
![]() . In the quantum mechanical literature, this type of quantity
goes by the name of Bargmann's invariant and its connection to the
geometric phase was made clear by Samuel & Bhandari (1988). With
some work, one can give a general proof that the closure phase (phase
of
. In the quantum mechanical literature, this type of quantity
goes by the name of Bargmann's invariant and its connection to the
geometric phase was made clear by Samuel & Bhandari (1988). With
some work, one can give a general proof that the closure phase (phase
of ![]() ) is equal to half the solid angle subtended at the centre
of the Poincaré sphere by the points represented by
) is equal to half the solid angle subtended at the centre
of the Poincaré sphere by the points represented by ![]() ,
,
![]() , and
, and ![]() on the surface of the sphere. For the case
where the polarization state of the three antennas are same, this
phase is zero in general. However, when the polarization states of
the antennas are different, this phase is non-zero.
on the surface of the sphere. For the case
where the polarization state of the three antennas are same, this
phase is zero in general. However, when the polarization states of
the antennas are different, this phase is non-zero.
The well known result that an arbitrary polarization state can be
represented as a superposition of two orthogonal polarization states
translates to representing any point on the Poincaré sphere by the
superposition of two diametrically opposite states on a great circle
passing through that point. For example, circular polarization can be
expressed by two linear polarizations, each with intensity
![]() . In the context of the present work, the nominally
circularly polarized antenna maps to a point away from the equator on
the Poincaré sphere (it would be exactly on the pole if it is purely
circular) while the rest of the antennas map close to the equator
(they would be exactly on the equator if they are purely linear and
map to a single point if they were also identical). The visibility
phase due to the extra baseline based term in Equation 7.3 due
to polarization mis-match is a consequence of the Pancharatanam phase
mentioned above. This phase, on a triangle involving the circularly
polarized antenna, will be close to the angle between the two linear
antennas. For example, if
. In the context of the present work, the nominally
circularly polarized antenna maps to a point away from the equator on
the Poincaré sphere (it would be exactly on the pole if it is purely
circular) while the rest of the antennas map close to the equator
(they would be exactly on the equator if they are purely linear and
map to a single point if they were also identical). The visibility
phase due to the extra baseline based term in Equation 7.3 due
to polarization mis-match is a consequence of the Pancharatanam phase
mentioned above. This phase, on a triangle involving the circularly
polarized antenna, will be close to the angle between the two linear
antennas. For example, if
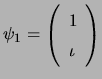 ,
,
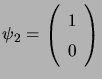 , and
, and
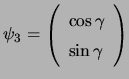 , the phase of
, the phase of ![]() will be
will be
![]() . This picture can be depicted by plotting the real and
imaginary parts of
. This picture can be depicted by plotting the real and
imaginary parts of
![]() , which is done in
Fig. 7.3. The circularly polarized antenna can be
clearly located in this figure as the set of point away from the
origin while the linearly polarized antennas as the set of points
close to the origin. The collection of points located away but almost
symmetrically about the origin represents the nominal right- and
left-circularly polarized feeds. Points on the equator, but
significantly away from the origin represents an imperfect linearly
polarized antenna. Note that the average closure phase between the
nominally linear antennas is close to zero, which defines the mean
reference frame in Fig. 7.3.
, which is done in
Fig. 7.3. The circularly polarized antenna can be
clearly located in this figure as the set of point away from the
origin while the linearly polarized antennas as the set of points
close to the origin. The collection of points located away but almost
symmetrically about the origin represents the nominal right- and
left-circularly polarized feeds. Points on the equator, but
significantly away from the origin represents an imperfect linearly
polarized antenna. Note that the average closure phase between the
nominally linear antennas is close to zero, which defines the mean
reference frame in Fig. 7.3.