Real data

150 MHz data

Engineering measurements for polarization isolation at 150 MHz for the GMRT show significant polarization leakage in the system. We therefore used leaky antsol to calibrate the data from the Galactic plane phase calibrator 1830-36 which is known to be less than $0.2\%$ polarized at 1.4 GHz. The percentage polarization at 150 MHz is not known, but it is expected to decrease further and it was taken to be an unpolarized point source.

Fractional polarization leakage ( $\left\vert {\alpha_i^{\it q}}/{g_i^{\it p}}\right\vert$) of up to 100% was measured for most of the antennas, which is consistent with the estimated leakage measured from system engineering tests. Again, $\chi^2_\mathrm{a}$ and $\chi^2_\mathrm{l}$ were computed and the results are shown in Fig. 7.2. The 150-MHz GMRT band suffers from severe radio frequency interference (RFI). The sharp rise in the value of $\chi^2_\mathrm{a}$ around sample number 10 is due to one such RFI spike. This spike is present in the total power data from all antennas at this time. On an average, the $\chi ^2$ reduces by $\sim60\%$ when leakage calibration is applied ( $\chi^2_\mathrm{l}$). This is consistent with polarization leakage being a major source of non-closure at this frequency.

Figure 7.2: Figure showing the results using GMRT data at 150 MHz for the compact Galactic plane source 1830-36. The top curve is the value of $\chi ^2$ using the classical antsol ( $\chi^2_\mathrm{a}$). The bottom curve is the value of $\chi ^2$ using the leaky antsol ( $\chi^2_\mathrm{l}$) as a function of time.

L-band data with circular feed

The GMRT L-band feeds are linearly polarized. For the purpose of a VLBI experiment conducted in December 2000, the L-band feed of one of the antennas was converted to a circularly polarized feed. The rest of the L-band feeds were linearly polarized and we took this opportunity to measure correlations between the circularly polarized antenna with other linearly polarized antennas using the source 3C147. Two scans of approximately one hour long observations were done using the single side band GMRT correlator. This correlator computes only co-polar visibilities. With this configuration of feeds, visibilities between the circularly polarized antenna and all other linearly polarized antennas corresponds to correlation between the nominal X- and R-polarizations, labeled by RX, were recorded in the first scan. The polarization of the circularly polarized antenna was then flipped for the second scan to record the correlation between the nominal X- and L-polarization states, labeled by LX.

The VLA Calibrator Manual^10.3 lists the percentage polarization ( $\frac{\sqrt{Q^2 + U^2 + V^2}}{I}$) for 3C147 at L-band $<0.1\%$. The cross-polar terms in Equation 7.2, which are assumed to be zero, will therefore contribute an error of the order of $0.1\%$. These cross-polar terms will be, however, multiplied by gains of type ${g_i^{\it p}}{\alpha_i^{\it q}}^\star$. Since ${g_i^{\it p}}$ and ${\alpha_i^{\it q}}$ are both assumed to be uncorrelated between antennas, this error will manifest as random noise in Equation 7.3. Within the limits of other sources of errors, the source 3C147 can therefore be considered to be a completely unpolarized source.

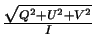Figure 7.3: Figure showing the results using visibilities with one circularly polarized antenna and all other linearly polarized antennas at L-band. The x- and y-axis denote the real and imaginary parts of ${\alpha_i^{\it q}}/{g_i^{\it p}}$ respectively. ${g_i^{\it p}}$ and ${\alpha_i^{\it q}}$ were solved for every integration time ($\sim 17 s$). All linearly polarized antennas are close to the origin in this plot. The solutions for the circularly polarized antenna (C03) are the set of points away from the origin (shown by open circles and triangles). The two sets of points for this antenna, separated from each other by $\sim 180^\circ$ are solutions for the right- and left-circular polarization channel. The points denoted by open circles are from correlation between the right- and left-circular polarization of C03 with nominal linear X-polarization of the other antennas (labeled as $\mathrm{C03^{RX}}$ and $\mathrm{C03^{LX}}$ respectively). The points denoted by triangles are from correlation of C03 with nominal Y-polarization of the other antennas (labeled as $\mathrm{C03^{RY}}$ and $\mathrm{C03^{LY}}$).

Results and Interpretation

The response of an ideal circularly polarized antenna to unpolarized incident radiation can be expressed as a superposition of two linear polarization states as $E_{i,\circ}^R = E_{i,\circ}^X e^{\iota \delta} + E_{i,\circ}^Y e^{-\iota \delta}$ where, the superscripts $R$, $X$ and $Y$ denote the right circular and the two linear polarization states respectively. $\delta$ is half the phase difference between the two linear polarization states and is equal to $\pi/4$ for right-circular polarization and $-\pi/4$ for left-circular polarization. Writing the general Equation 7.1 for right-circularly polarized antenna as $E^R_i=g^R_i E^R_{i,\circ} + \alpha_i^L E^L_{i,\circ}$ and substituting for $E_{i,\circ}^R$ and $E_{i,\circ}^L$ we get

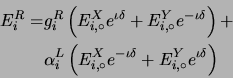$$\begin{split}E^R_i =& g^R_i \left(E^X_{i,\circ} e^{\iota \del... ...ta \delta} + E^Y_{i,\circ} e^{\iota \delta} \right) \end{split}$$ (10.10)

Equation 7.3 for the case of correlation between a circularly polarized and a linearly polarized antenna, with polarization leakage in both the antennas, can be written as

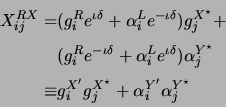$$\begin{split}X^{RX}_{ij} =& (g_i^R e^{\iota \delta} + \alpha_... ...^{X^\star} + \alpha_i^{Y^\prime} \alpha_j^{Y^\star} \end{split}$$ (10.11)

where $g_i^{X^\prime} = g_i^R e^{\iota \delta} + \alpha_i^L e^{-\iota \delta}$ and $\alpha_i^{Y^\prime} = g_i^R e^{-\iota \delta} + \alpha_i^L e^{\iota \delta}$. The leaky antsol solutions for the circularly polarized antenna in this case will correspond to $g_i^{X^\prime}$ and $\alpha_i^{Y^\prime}$.

Let $P_i=\alpha_i^Y/g_i^X$ ( $P_i=\alpha_i^{Y^\prime}/g_i^{X^\prime}$ for the circularly polarized antenna). Then, the amplitude of $P_i$ is a measure of the fractional polarization leakage in the antenna while the phase of $P_i$ gives the phase difference between the signal from one of the feeds and the leaked signal from the other feed. For an ideal circularly polarized antenna, $\vert P_i\vert\approx 1$. A plot of the real and imaginary parts of this quantity for all antennas should therefore clearly show $P_i$ for the circularly polarized antenna with an amplitude of 1 and at an angle of $\pi/2$ with respect to the nominal X-axis.

The real and imaginary parts of $P_i$ for all antennas from this experiment are shown in Fig. 7.3. The solutions were computed for every integration cycle of $\sim 17$ sec and the points on this plot represent the tip of phasor $P_i$. The collection of points near the origin are for all the linearly polarized antennas while the collection of two sets of points away from the origin, approximately an angle of $\pi$ from each other, are for the circularly polarized antenna. The solutions found by leaky antsol match the expected results quite well. This therefore constitutes a reasonably controlled test with real data showing that the solutions indeed provide information about the polarization leakage in the system.

This experiment however provides much more information about the polarization properties of the antenna feeds used. The collection of points in the first quadrant denoted by open circles are the values of $P_i$ derived from the correlation between the nominal right-circularly polarized signal and the linearly polarized signals along the nominal X-axis from all other antennas. Points in the third quadrant are similarly derived using the left-circular signals. The set of points denoted by triangles in the second and fourth quadrant are derived using correlations of right- and left-circularly polarized signals with the linearly polarized signals along the nominal Y-axis from all other antennas.

A larger spread in the solutions using the left-circularly polarized signals indicates that the closure noise (from other unknown sources) in these signals is higher. The fact that the amplitude of $P_i$ derived using the right-circularly polarized signals is $\approx 0.5$ indicates that the nominal circularly polarized feed is in fact elliptically polarized with this axial ratio. The spread of $\pm 1-2\%$ about the origin is indicative of polarization leakage at the level of few percent in the linearly polarized antennas as well. The leakage in one of the linearly polarized antennas is significantly larger ( $\approx 4\%$). Since this kind of data is routinely taken on primary calibrators during GMRT observations for synthesis imaging, leaky antsol provides a useful diagnostic of system health, polarization performance and numbers needed to correct the data in high accuracy work.

The following test was also carried out to check that the closure phase on a triangle involving the circular feed was indeed mainly due to polarization effects. The three baselines making up this triangle were flagged as bad baselines from the input data and a new solution found for the gains and leakages of all antennas. This solution predicted the same closure phase (to within errors) as actually observed.