Non-uniqueness of solutions

We discuss the non-uniqueness of the solutions of Equation 7.3, and possible convenient conventions for choosing a specific solution. One obvious degeneracy is that multiplication of all the $\alpha$'s by one common phase factor independent of antenna, and all the $g$'s, by another, in general different, common factor, does not affect the right hand side of Equation 7.3. Also, the equation was written in a specific basis, say right and left circular. But it would have had the same form when using any other orthogonal pair as basis. Hence we are free to apply this change of basis to one solution to get another solution of Equation 7.3. Under such a change, the coefficients transform according to

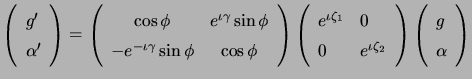$$\left( \begin{array}{ll} g^\prime \alpha^\prime \end{array}... ...\end{array} \right) \left( \begin{array}{ll} g \alpha \end{array} \right)$$ (10.12)

It is easy to verify that under this change, $\alpha_i^\prime \alpha_j^{\star\prime} + g_i^\prime g_j^{\star\prime}=\alpha_i \alpha_j^\star+g_i g_j^\star$. Clearly, since $\chi ^2$ is unchanged by these transformations, an iterative algorithm will simply pick one member of the set of possible solutions, determined by the initial conditions. Having found one such, one could apply a suitable transformation to obtain a solution satisfying some desired condition. For example, if one has nominally linear feeds, one might impose the statistical condition that there is some mean linear basis with respect to which the leakage coefficients will be as small as possible. Such a condition has the advantage that a perfect set of feeds is not described in a roundabout way as a set of leaky feeds with identical coefficients, simply because the basis chosen was different. Carrying out the minimization of $\sum\left\vert g_i\right\vert^2$ by the method of Lagrange multipliers, subject to a constant $\chi ^2$, we obtain the condition that $\sum\alpha_i^*g_i=0$. This solution can be interpreted as requiring the leakage coefficients to be orthogonal to the gains, and is reasonable when we think about the opposite kind of situation, when the leakages are "parallel" to the gains, i.e. identical apart from a multiplicative constant. In such a case, we would obviously change the basis to make the new leakage zero. If we have a solution which does not satisfy this orthogonality condition, we can bring it about in two steps. First, choose an overall phase for the $\alpha$'s so that $\sum \alpha_i^\star g_i$ is real. Then, carry out a rotation in the $g - \alpha$ plane by an angle $\theta$ satisfying $\tan \theta=\sum \alpha_i^* g_i /(\sum(g_i g_i^\star -\alpha_i \alpha_i^\star)$. This rotation has been so chosen that it makes the leakage "orthogonal" to the gains, in the sense required above. Even after this is done, we still have the freedom to define the phase zero independently for the two orthogonal states. This is because we are only dealing with unpolarized sources. Of course, if we had a linearly polarized calibrator, the relative phase of right and left circular signals would not be arbitrary.

A more geometric view of this degeneracy is obtained when we think in terms of the Poincaré sphere representation of the states of polarization of all the feeds. The cross correlation between the outputs of two feeds, both of which receive unpolarized radiation, has a magnitude equal to the cosine of half the angle between the representative points on the sphere. Measurements of all such cross correlations with unpolarized radiation fixes the relative geometry of the points on the sphere, while leaving a two parameter degeneracy corresponding to overall rigid rotations of the sphere. This degeneracy can be lifted by the measurement of one polarized source at many parallactic angles.

Finally, we note that for the purpose of correcting the observations of unpolarized sources for the effects of non-identical feed polarization, the degeneracy is unimportant, because the correction factor is precisely the right hand side of Equation 7.3 which is unaffected by all the transformations we have discussed.