Lecture 8 - Atomic Spectra (2/4/99)
 Stellar Classes --- | ---
Statistical Mechanics
Stellar Classes --- | ---
Statistical Mechanics

 Reading:
Reading:
Chapter 8-2, 8-3 (ZG4)
Notes:
pages 27 - 33
 |
Key Question: |
What is the origin of spectral lines
in stars?
|
|---|
 |
Key Principle: |
The Bohr model
|
|---|
 |
Key Problem: |
What are the energy levels in hydrogen
and how are they related to line series?
|
|---|
Investigations:
- The Bohr Atom
- What is the Coulomb electrical force?
- How should the hydrogen atom behave, in analogy with
a two body gravitational system?
- What is the classical energy for an atomic orbit of
radius r?
- What is the quantum of angular momentum?
- What is the Bohr radius?
- What is the energy of an atomic orbit of principal
quantum number n?
- Particles and Waves
- What is the de Broglie wavelength for a particle?
- How is the quantization of angular momentum related to the
wave nature of the electron?
- What is the spin angular momentum of an electron?
- How many electrons can be in the same orbital state?
- How many electrons can fit on a "shell" n?
- How many quantum numbers are needed to fully specify an
electron?
- What is the atomic basis of the periodic table of the elements?
- The Hydrogen Line Spectrum
- What is the ground state of hydrogen?
- What is the ionization energy of hydrogen?
- At what wavelength is the Lyman limit?
- What is the significance of the Lyman and Balmer series?
- At what wavelength is Lyman alpha line? H alpha?
- Ionization and Molecules
- What are the ionizations states of H I and H II? He I, He II, He III?
- How much energy does it take to ionize He I to He II? He II to He III?
- Why are He II and H I similar?
- What species and ionization states of elements are found in the solar
spectrum?
- Do molecules have energy levels like atoms?
- What are the rotational and vibrational states of
a molecule?
- What are molecular bands in spectra?
- What part of the spectrum do most molecular vibrational and rotational
lines lie in?
Particles and Waves:
Just as electromagnetic waves of light are also particles (photons),
all particles such as electrons and protons are waves! It turns out
that a particle of momentum p has a wavelength of
l = h / p = h / mv
so more massive particles have smaller wavelenghths. This property is used
(sort of) in electron microscopes, which act like normal microscopes
except using the wave nature of electrons instead of light. Because the
wavelength of an electron wave is very very small, it can see smaller things
than normal light based microscopes.
When we put an electron into an "orbit" around an atomic nucleus,
we must consider the wave-nature. To pack the electron wave into orbit
we must put it in as a standing wave with an integer number of
wavelengths around the circumference:

These integer numbers of waves cause quantization of the orbits.
The Bohr Atom: Orbital Radii and Energy Levels
The condition that an electron wave not interfere with
itself on an orbit means that there must be an integer number, say n,
wavelengths on an orbit. The smallest allowed orbit contains a single
wavelength. We wish to compute the radius and Energy of the orbits in the
hydrogen atom. This was done by Niels Bohr. This gives the relation that
2  r = n
r = n
 e
e
where lambda_e is the wavelength of the electron and r is the orbital
radius.
From the physicist de Broglie, we know that the wavelength of
an electron is proportional to the inverse of its momentum:
 e = h / m v,
e = h / m v,
where m is the electron mass and v is the velocity
of the electron, and h is Planck's constant.
Thus, we find the velocity of the electron to be given by:
v = (h/2 ) (n/ m r)
) (n/ m r)
or equivalently, the orbital angular momentum
L = m v r = n 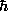
where "h-bar" is
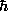 = (h/2
= (h/2 ).
).
Thus, in the quantum atom, the orbital angular momentum L is quantized,
with the quantum of angular momentum being h-bar! This is a profound
result, and is as important for atomic physics as the quantization of
light E = hf was for blackbody radiation.
Just like when we wanted to derive Kepler's law from the gravitational
force we used the centripetal acceleration to give us the velocity,
we do the same here. We have the Coulomb force
F = e2/r2
where we have absorbed the usual MKS electrostatic constant into the
units for the electron and proton charges +e and -e
e2 / 4
 0 --> e2.
0 --> e2.
The centripetal force is just F = m v^2 / r, so we equate
( e2 / r2 ) = (m v2 / r)
and thus we find:
v2 r = e2 / m
Substituting in our expression for the velocity in the above equation
gives
( n 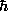 /mr )2 r
= (e2 / m)
/mr )2 r
= (e2 / m)
or
rn = n2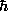 2
/ me2.
2
/ me2.
If we then define the Bohr radius
a0 = 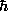 2 / m e2
2 / m e2
then we find the simple relation for the radius of orbit n:
rn = a0 n2
The orbital radii of the hydrogen atom, quantised by the number
of wavelengths n:

To find the energy levels, we need to know what the energy of a
moving particle under a force is. It turns out it has two terms
due to the motion and due to the force:
E = mv2/2 - e2/r
The first term (m v^2/ 2) is called the kinetic energy and
is the energy carried in the motion of the electron, like the energy
in a thrown baseball which you feel when it hits you.
The second term (-e^2/r) is called the potential energy, and
it is the energy "contained" in the electric force that you must
work with or against to move an electron closer or farther from the
nucleus. It has the opposite sign to the kinetic energy because
the total energy is conserved, you cant make or destroy energy
out of nothing. Thus if you speed up an electron (increase its
kinetic energy) you must draw it from the potential
energy due to the electric force (decrease its potential energy).
If we compute the energy E, we see that since v^2 r = e^2 / m
from the centripetal force, then L
E = - e2/2r
Substituting in r_n = a_0 n^2, then easily we find:
E = -e2 / (2a0n2)
If we define the energy at the ground state to be
E0 = e2/2a0
the Rydberg Energy for hydrogen (sometimes we write E_R instead
of E_0), then
E = - E0 n-2.
Thus, the energy levels are spaced like the inverse square of the
level number n, while the radii are spaced like the square
of n.
The energy levels of the hydrogen atom:
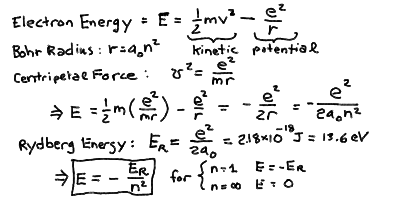
From all the constants you can compute the values of the Bohr Radius
a_0 = 5.29 x 10^-11 m = 0.053 nm = 0.53 Å, and the Rydberg energy
E_0 = 2.18 x 10^-18 Joules = 13.6 eV.
We have defined a more convenient unit of energy: the electron volt
(eV). This is the energy gained by an electron accelerated through a voltage
difference of 1 volt (like from a battery). It is very tiny
( 1eV = 1.602 x 10^-19 J ), but more convenient for the energies encountered
in atomic physics.
In this energy level scheme, we see that an electron at rest infintely
far away from the proton (in the absence of any other atoms!) has
an energy of E = 0 (for n = infinity). The ground state
n = 1 has an energy E = -13.6 eV. Thus, it takes an energy
of 13.6 eV to remove an electron in the ground state from the hydrogen
atom.
Hydrogen Energy Levels and Line Series
The Rydberg formula for the transition wavelengths between two
energy levels m and n in hydrogen:
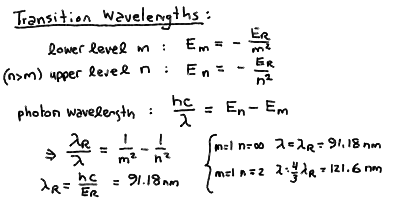
The line series of hydrogen corresponding to transitions between
upper levels and lower levels:
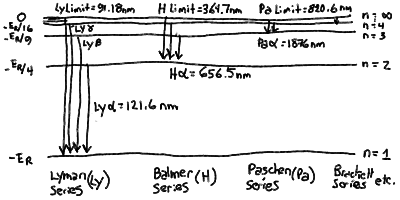
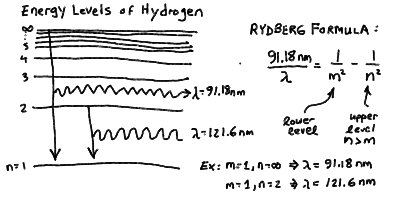
In particular, the Rydberg formula gives the spaceing for the
hydrogen series:
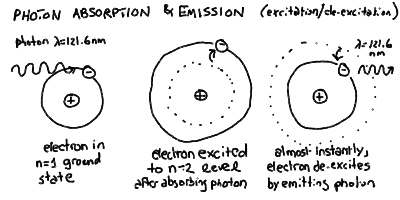
Jumping between these levels can be initiated by absorption of
a photon of the correct energy, but the atom quickly returns to
its de-excited state emitting a photon of the same energy:
Electron Orbitals and Quantum Numbers
The quantum numbers of electrons in the atom:

The configuration of electrons in the different l orbitals:

Atomic Spectra in Outline:
- The Atom
- Atoms are made up of subatomic particles: electrons, protons, and
neutrons. Electrons, light particles that carry negative
charge, were discovered by J.J. Thomson in 1897, and Ernest Rutherford
discovered in 1911 that the positive charge in the atom was
concentrated in a tiny nucleus. Later, the nucleus was shown
to contain positive protons, and charge neutral neutrons.
- In Rutherford's model of the atom, the nucleus is surrounded by
a cloud of electrons constantly in motion.
- Protons and neutrons are the most massive subatomic particles, though
even they are tiny. Both have about the same mass: 1.67 x 10^-24 g.
- Electrons are much less massive, with a mass of about 1/1836 of the
proton mass.
- Atoms are mostly empty space. The nucleus itself contains most of
the mass, but is only about 10^-6 nm ( 10^-15 m) in size! The
extent of the electron cloud is about 0.1 - 0.5 nm.
- The electric forces between the oppositely charged electrons and
protons hold the atom together. The protons and neutrons in the
nucleus are held together by the strong nuclear force, which can
overcome the mutual repulsion of the like-charged protons.
- Even though atoms are mostly empty space, two atoms don't easily
pass through each other because of the electric forces of the
electron clouds. The solidity of matter is purely the doing of
electric forces. When you press your hand against a tabletop,
it is actually the electron clouds in the atoms of your hand pushing
electrically against the electron clouds in the atoms of the table.
- Why don't all atoms just repel each other and fly apart, like a gas?
If you bring two atoms close enough together, with the right
configuration of electron clouds in each, then the two separate
atoms can merge, sharing electron clouds - this is called a
molecule.
- Molecules can fit together into solids (and to a lesser extent
liquids) by very very weak inter-molecular forces left over in
the outermost electron clouds. The physics of the attractive forces
between atoms and molecules is what makes chemistry work.
- Coulomb Forces and Electron Orbits
- The electric force, as specified by Charles Coulomb (1736-1806)
is given by the inverse-square law:
F = C q1 q2 r-2
where q_1 and q_2 are two electric charges, r the distance between them
and C a constant having to do with the units of charge (and distance).
- Notice any similarity to something we already know? Indeed, the
electric Coulomb force has the same dependence as the gravitational
force of Newton, with the charges standing in for masses.
- One difference with gravity is that electric charge can have both
positive and negative sign, so the electric force is either attractive
or repulsive. Opposite charges attract - like charges repel.
- The gravitational force, on the other hand, is strictly attractive.
There are no negative masses, and thus there is no gravitational
repulsion (anti-gravity).
- Since the electric and gravitational forces look the same
mathematically, then we might expect them to behave similarly
physically. Thus, we would expect that electrons would orbit
the nucleus much like a planet orbits the Sun!
- Just like it takes energy to send a spaceship out into a higher
orbit, and that if you take some of the energy of motion away
from a spaceship (say through friction with the atmosphere) it
will drop to a lower orbit, then so also does the energy of
the electron orbit rise with increasing distance from the nucleus.
- If we carry on our analogy with planets, then we might expect that
any orbit at all could be obtained for an electron, as long as
you gave it the proper energy.
- The energy of an electron can be changed by emitting or absorbing
a photon. This is, as we mentioned before, how the electromagnetic
force is transmitted, through the intermediation of photons. If
a photon is absorbed by the electron, then the outgoing electron
carries the energy and momentum of both the incoming electron and
photon. If an electron emits a photon, then its energy and momentum
are distributed between the outgoing electron and photon.
- Thus an electron in an atom can absorb a photon and jump to a higher
orbit, or emit a photon and fall to a lower orbit. The change in
orbit is given by the energy of the photon.
- There is one (at least one) conceptual problem with this. It was
known for quite a while that an accelerating electric charge radiates
electromagnetic radiation, that is, photons. This is how we use
an oscillating electric current to generate radio waves. This is also
why very hot things emit light - the moving atoms jiggle around the
electrons which emit photons. In any event, we would expect the
orbiting electrons, accelerated by the centripetal accleration of
the electrical force, to cause them to radiate photons and thus lose
energy and spiral in toward the nucleus. This was a big puzzle in
20th century physics.
- Quantization and Energy Levels
- Physics is a series of a few themes played over and over.
- It was mentioned before, in discussing the particle and wave nature
of a photon and light, that particles such as electrons have a
wave nature also. This was normally hard to detect, since the
wavelength was inversely proportional to the momentum of the particle.
Electrons can have wavelengths of less than a nanometer, and thus
can make useful electron microscopes that can see very tiny
things.
- It is obvious that in the tiny orbits in atoms, that we must take into
account the wave nature of the electron! That is, it is not an
orbiting particle like a planet that we must work with, but our task
is to fit an electron wave into a confined orbit in a way that makes
sense.
- According the the physicist de Broglie, particles
correspond to waves with wavelength given by
L = h / p
(where p is the momentum, and h is Planck's constant)
and frequency
f = E / h
(just like light).
- What we have learned from dealing with light waves is that when you
bring parts of a wave together, then unless you are careful, it will
interfere with itself and cancel out. In fact, if you try
drawing a sinusoidal wave on a circlular orbit, then unless you adjust
the wavelength, you will arrive back at the starting point
out of phase and as you draw the wave around and around the
orbit, it will cancel out completely!
- Thus, you can see graphically that the only allowed wave orbits are
those with an integer number of wavelengths in the circumference
(see drawing below). Then, the wave wraps around and around always
in phase with itself - this sort of wave pattern is called a
standing wave. This is how a plucked string generates a
note of musical sound, it is allowed to oscillate only such that
a standing wave of motion is produced.
- Thus, we would expect that orbits are quantized
in a special way so that an integer number of standing electron
waves, say n, will fit on the circumference
2 Pi r = n
where the integer n = 1, 2, 3, ... and so on.
Thus we would expect only certain quantized energy
levels to exist in an atom, and thus only photons of special energies
corresponding to the differences between these levels to be absorbed
and emitted by the electrons.
- The different allowed orbits are roughly spherical (not circles) and
are called electron shells. Even though they are spheres,
not closed circles, our wave arguments still hold. The exact orbital
pattern of an electron wave determines the ability of an atom to
make molecules, because as you can see if it is concentrated into
a circle, then the positive proton can make its attractive force
felt in the perpendicular direction along the poles of the orbit!
It also turn out that we can pack in more than a single electron
in one shell. How many you can put in without them interfering with
each other is an important property of atomic structure.
We will discuss these topics more in the next lecture.
- The physics of the actions of wave-particles, and of quantized
states that arise when you work with them, is called quantum
mechanics. This subject was pioneered in the early parts of
this century, and has caused a revolution in our understanding of
the nature of the Universe.
- So, in our quantum atom, an electron can absorb a photon of
specific energy and jump to a higher energy shell. However, it
turns out that it will almost immediately emit a photon and
jump back down to the original level, or one lower if possible,
emitting a photon in the process.
- You can see there is a minimum-energy orbit corresponding to
a single wavelength on the orbit. If we number the shells outward
from the nucleus by their integer number of waves, we would call
this the n = 1 orbit.
- Because rules of quantum mechanics allow us to only put a certain
number of electrons in each orbit, there is an atomic state where
all the lowest available orbits are filled. This is the lowest
energy state of the atom, and is called the ground state.
- If an atom is in the ground state, and one of its electrons absorbs
a photon and jumps to a higher-energy orbit, then we say that this
atom is now in an excited state. It almost immediately emits
a photon of the same energy and de-excites back to the ground
state. It would take a continuous bombardment by photons (or
collisions) to keep atoms in an excited state for any length
of time.
- What are the energy levels, and thus the allowed wavelengths of
emitted and absorbed photons, for a simple atom like hydrogen?
It turns out that there is a simple formula, called the Rydberg
formula, that gives this (see below).
- Note that there is a finite energy difference between the lowest orbit
and an electron orbiting at infinity. For hydrogen, this corresponds
to a wavelength of 91.18 nm. If a photon of this wavelength or shorter
is absorbed by an electron in the ground state, it will be knocked out
of the atom altogether! Note that a jump from the n = 1
to the n = 2 levels corresponds to a wavelength of 121.6 nm.
- In the next lecture, we will look in more detail at the energy
level emitted spectrum of the hydrogen atom.
- The Danish physicist Niels Bohr (1872-1962) devised a more or less
correct vision of the atom, though without the notion of waves or
quantum mechanics. This classical Bohr atom with quantized orbits
is often still used as a toy model.
Key Problems:
- Why don't electrons radiate away energy and spiral into the nucleus?
- What are wavelengths of the Lyman and Balmer series of H I and He II?
 Prev Lecture ---
Prev Lecture ---
 Next Lecture ---
Next Lecture ---
 Astr12 Index ---
Astr12 Index ---
 Astr12 Home
Astr12 Home
smyers@nrao.edu
Steven T. Myers
 Stellar Classes --- | ---
Statistical Mechanics
Stellar Classes --- | ---
Statistical Mechanics

 Stellar Classes --- | ---
Statistical Mechanics
Stellar Classes --- | ---
Statistical Mechanics

 Reading:
Reading: 



 r = n
r = n
 e
e
 e = h / m v,
e = h / m v, ) (n/ m r)
) (n/ m r)
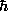
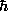 = (h/2
= (h/2 ).
).

 0 --> e2.
0 --> e2.
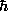 /mr )2 r
= (e2 / m)
/mr )2 r
= (e2 / m)
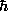 2
/ me2.
2
/ me2.
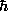 2 / m e2
2 / m e2

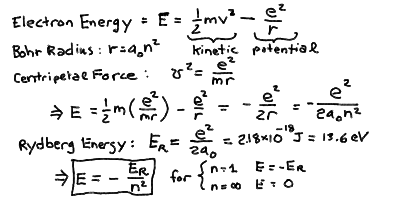
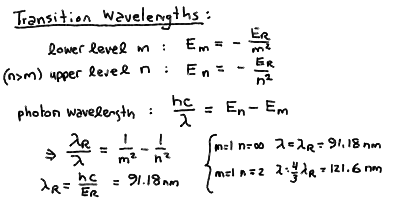





 Prev Lecture ---
Prev Lecture ---
 Next Lecture ---
Next Lecture ---
 Astr12 Index ---
Astr12 Index ---
 Astr12 Home
Astr12 Home