Lecture 9 - Statistical Mechanics (2/11/99)
 Atomic Spectra --- | ---
Radiative Transfer
Atomic Spectra --- | ---
Radiative Transfer

 Reading:
Reading:
Chapter 8-4, 8-7 (ZG4)
Notes:
pages 34 - 38
The Sun and prominence from NASA's Skylab space station on
December 19, 1973. (Courtesy NASA)
 |
Key Question: |
What determines the energy state
of atoms in a gas?
|
|---|
 |
Key Principle: |
The Boltzmann and Saha Equations
|
|---|
 |
Key Problem: |
What fraction of hydrogen in
the Solar Photosphere is ionized?
|
|---|
Investigations:
- States - The Boltzmann Distribution
- How does the equilibrium between excitation and
de-excitation determine the relative populations
in different atomic energy states?
- What are the electronic energy levels in an atom?
- What is the root-mean-square kinetic energy per particle
for a gas at temperature T?
- What is the expected ratio between numbers of atoms in
two atomic energy states?
- What is the significance of the Boltzmann factor
e-E/kT
- What is the mulitiplicity or statistical weight g of
an energy level? How does that effect the populations?
- Where does the Boltzmann factor come from, and how is it related
to the central limit theorem?
- What is statistical physics?
- At what temperature T is the Boltzmann factor on e-fold down for
E = 1 eV?
- Where else does the Boltzmann factor apply?
- Ionization - The Saha Equation
- What is ionization equilibrium?
- What do the ionization states I, II, III, etc signify?
- What are the ionization states of hydrogen? Helium?
- What is the ionization potential of hydrogen?
- How does the Boltzmann factor affect the ionization?
- How does the ionization depend upon the electron density?
- What is the statistical weight factors for ionization?
- What is the Saha equation?
- Do you expect the solar photosphere to be ionized?
- How do you compute the fractional ionization of a gas?
- What is the electron pressure in the solar photosphere?
- What is the expected fractional ionization of the solar photosphere?
- The Balmer Series - Boltzmann + Saha Equations
- What is the Balmer series in hydrogen?
- On the population of which level does the Balmer series line strength
depend?
- At what temperature should the Balmer series be the strongest?
- Why does the Balmer series fade at high and low temperatures?
- How can you use line strengths to find conditions in an atmosphere?
- The Solar Photosphere
- If the Sun is just a ball of hot gas, why does it appear to have a
distinct surface?
- What is above and below the surface of the Sun? What keeps them apart?
- What do we mean by the photosphere?
- What do we see when we look at the photosphere of the Sun?
- Radiative Transfer I - The Problem
- What can happen to photons on their way through a medium?
- Why do we need only consider absorption and emission,
and not scattering separately?
- What do we mean by a "beam" of photons?
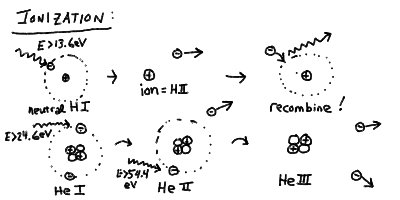
Ionization States
The process of ionization and recombination and the ionization states
of hydrogen and helium:
The Boltzmann Equation
The ratio of the number density (in atoms per m^3) of atoms in
energy state B to those in energy state A is given by
NB / NA = ( gB / gA )
exp[ -(EB-EA/kT ]
where the g's are the statisical weights of each level (the number of
states of that energy). Note for the energy levels of hydrogen
gn = 2 n2
which is just the number of different spin and angular momentum states
that have energy En.
The Saha Equation
The textbook is a little confusing on this subject, as they just give
in (8-31)
Ni+1 / Ni = A Ne-1
(kT)3/2 exp[ - i/kT ]
i/kT ]
but don't say what A is! In class, we gave the full equation
Ni+1 / Ni = ( 2Qi+1 /
NeQi )
( 2 mekT / h2 )
exp[ -
mekT / h2 )
exp[ - i/kT ]
i/kT ]
where Q is the partition function for the two ionization states (normalized
to the ground state)
Q = g1 +  n=2
gn
exp[ En - E1 / kT ]
n=2
gn
exp[ En - E1 / kT ]
which numerically becomes
Ni+1 / Ni = ( 2.41 x 1021 m-3
/ Ne ) ( 2Qi+1 / Qi ) T3/2
exp[ - i/kT ]
i/kT ]
(note that for HII Q=1 and HI Q=2 so the partition funtion terms go
to unity). We also used the fact that the electrons can be seen to
form a gas
Pe = Ne k T
so we can write the Saha equation as
Ni+1 / Ni = ( 3.33 x 10-2 Pa
/ Pe ) ( 2Qi+1 / Qi ) T5/2
exp[ - i/kT ]
i/kT ]
since the density and temperatures vary through most stellar atmospheres
but the are roughly isobaric.
Note that the Saha equation is just an application of the
Boltzmann equation to the case of ionization states! If you are
trying to compute the occupancy of different energy states in the same
ionization state (be H I, He I, He II, etc) then you need to use
the Boltzmann equation. If you are trying to compute the relative fraction
of atoms in one particular energy state of one particular ionization state
to the total number in all energy and ionization states, then you need
to use both equations!
For example, to calculate the fraction in the n=2 state of H_I to the total
number density N, which can be either in the ionization state H I (any n) or H
II. Since we found in class (and you can demonstrate easiy) that almost all
of the H I atoms are in the n=1 ground state, N_1 ~ N_I, and thus
N2/N = ( N2/N1 ) /
( NI/N1 + NII/N1 )
 ( N2/N2 /
( 1 + NII/NI )
( N2/N2 /
( 1 + NII/NI )
on which you can use the Boltzmann equation (for N_2/N_1) and the
Saha equation (for N_II/N_I).
Types of Spectra: Continuum, Emission, Absorption
Three types of spectra:

More Atomic Spectra in Outline:
- The Bohr Atom: Orbital Radii and Energy Levels
- For an electron wave not to interfere with itself, there must
be an integer number n wavelengths on an orbit. The
smallest allowed orbit contains a single wavelength.
- The radius of the orbit is:
r = (h/2Pi)2 n2 /
(m e2)
(where we absorb the Coulomb constant into e).
- The radius for n = 1 is the Bohr radius:
a0 = h2 / (4 Pi2
m e2)
- Then,
r = a0 n2
- The energy of a moving particle under a force is:
E = (m v2 / 2) - (e2 / r)
- The first term (m v^2/ 2) is the kinetic energy, and
the second term (-e^2/r) is the potential energy.
- Using the Coulomb and centripetal forces, we find:
E = - e2/2r = -e2 /
(2 a_0 n2)
- Thus, E = - E_R / n^2 where E_R = e^2 / (2 a_0) is
the Rydberg Energy for hydrogen.
- Thus, the energy levels are spaced like the inverse square of the
level number n, while the radii are spaced like the square
of n.
- From all the constants you can compute the values of the Bohr Radius
a_0 = 5.29 x 10^-11 m = 0.053 nm, and the Rydberg energy
E_R = 2.18 x 10^-18 Joules = 13.6 eV.
- We define the the electron volt (eV) as
the energy gained by an electron accelerated through a voltage
difference of 1 volt (like from a battery).
1 eV = 1.602 x 10-19 J
- An electron at rest infinitely far away from the proton
(n = infinity) has E = 0, while the ground state
n = 1 has an energy E = -13.6 eV.
- It takes an energy of 13.6 eV to remove an electron in the
ground state from the hydrogen atom (ionization, see below).
- Hydrogen Energy Levels and Line Series
- Now that we have the energy levels of hydrogen, we can compute
easily the wavelengths of light emitted and absorbed on
transitions between different orbits.
- These are called spectral lines because in the spectrum
of a star (the brightness versus frequency) these show up as narrow
"lines" at specific wavelengths.
- The energy of a photon of wavelength L is just E = h c / L.
The energy difference between a lower level m and an
upper level n > m is just
( En - Em ) = ER
( 1/m2 - 1/n2 )
- Thus, the wavelength L corresponding to this difference is given by:
(h c / Lmn) = ( En - Em )
- If we define the Rydberg wavelength L_R = (h c / E_R) = 91.18 nm,
then:
LR / Lmn =
1/m2 - 1/n2
- We see immediately that the largest energy transition is from
the ground state m=1 to n=infinity (13.6 eV) has
a wavelength of 91.18 nm. Photons of this wavelength or shorter
will remove the electron from hydrogen entirely (see Ionization
below). All other hydrogen lines have wavelengths longer than this.
- There are series of lines corresponding to transitions between
each lower level m and all upper levels. The series for
the ground state m=1 and all higher levels is called the
Lyman Series. The longest Lyman line corresponds to an
upper level n=2, and from our formula can be seen to have
a wavelength of 121.6 nm. All the other Lyman lines have wavelength
between this and the Lyman limit of 91.18 nm.
- These series of lines have a charateristic spacing that converge
closer and closer to the limit for n=infinity.
- The longest wavelength line in a given series is designated by
the Greek letter Alpha. The next is Beta, then Gamma, then Delta,
and so on. The Lyman series is thus Ly Alpha (121.6 nm), Ly Beta
(102.6 nm), Ly Gamma (97.25 nm), and so on. We abbreviate Lyman
as Ly.
- From those wavelengths, you can see that the Lyman line series
is hard to see since it is in the ultraviolet part of the spectrum
which is absorbed by the Earth's atmosphere. It is much easier to
see the next series corresponding to a lower level m=2.
- The Balmer Series is between a lower level m=2 and
those above. The first line is H Alpha (the designation for Balmer
for historical reasons is H for Hydrogen) at 656.6 nm, with
H Beta (486.3 nm), H Gamma (434.3 nm), H Delta (410.3 nm) and so
on up to the Balmer limit of 364.7 nm.
- The Balmer lines are in the visible part of the spectrum and are
prominent in most stars.
- There are other series of lines, Paschen for m=3
( Pa Alpha = 1876 nm, limit = 820.6 nm) and Brackett for
m=4 ( Br Alpha = 4052 nm, limit = 1459 nm ). These
lines are in the infrared part of the spectrum and harder
to measure from the ground.
- As is common in this subject, astronomers are not content to use
normal units for wavelength like nanometers. They use the
Angstrom (A) which is just one-tenth of a nm, or
1 A = 10^-10 m, and so 10 A = 1 nm.
Thus, the wavelength of H Alpha is 6565 A, Ly Alpha is 1216 A,
and the Lyman limit is 912 A.
- The Bohr radius a_0 is 0.529 A. Most atoms are a few Angstroms
across.
- Ionization
- If a photon of short enough wavelength (high energy) is absorbed,
for example shorter than 91.18 nm for hydrogen, then the electron
is knocked clear out of the atom, and it is free to roam the universe
at will.
- This process is called ionization and can also be caused by
a strong enough collision. Ionization leaves behind a free electron,
and an atom that is now positively charged - and is called an
ion.
- The free electron can later (actually not very much later ususally)
recombine with this or another ion, since it is attracted by
the electric force.
- In multi-electron atoms, such as any other type of atom than
hydrogen, it takes more energy to knock out successive electrons
after you remove the first one. This is just because there is
more charge pulling on fewer electrons (which tend to screen each
other from the nucleus).
- Also, it takes more energy to remove electrons that are closer to
the nucleus, since they have a more negative energy E. It is always
the outermost, or the least tightly bound, electron that is first
removed upon ionization.
- Ionization states of atoms are designated by the chemical symbol
for the element (H=hydrogen, He=Helium, C=Carbon, etc) and a
Roman numeral (I=neutral, II=singly ionized, III=doubly ionized, etc.)
- Thus neutral hydrogen is H I, and ionized hydrogen (a proton and an
electron) is H II.
- Neutral Helium is He I, singly ionized Helium is He II (one electron
removed), and doubly ionized Helium is He III.
- It takes 13.6 eV to turn H I into H II. It takes 24.6 eV to turn
He I into He II, and another 54.4 eV to turn He II into He III.
The ionization energy of He 24.6 eV is slightly less than twice
hydrogen because of the screening of the other electron. The
ionization energy from He II to He III is four times 13.6 eV
because the energy goes as the charge squared, and He II looks like
hydrogen with a single electron, but more positive charge in the
nucleus.
- Electron Orbitals and Quantum Numbers
- We have established orbits, or electron shells, with
increasing radius from the nucleus
r = a0 n2
and increasing energy
E = -ER / n2
In some sense, we have labeled these orbits or states by
the magic number n, which increased from the ground
state n = 1.
- A good question was asked in class - we have been drawing the electron
orbit as a circle, like a planet's orbit. But atoms are spherical.
Should we take that into account?
- The answer to that is yes - in fact, it is crucial for the structure
of atoms and how atoms interact with each other. If orbits were
circular, then we can see that we can only put one electron on
a given shell without it interfering. It turns out if you compute
the number of separate waves that you can put on a spherical
shell at level n, you find that you can actually put
n^2 waves and still be able to tell them apart! (This is
like the surface area of the sphere goes like the radius squared.)
Thus, you can put more than one electron into each shell, as long
as you can tell them apart.
- The way you tell apart two electrons is by labeling them by a series
of quantum numbers, like we tell apart houses by addresses.
The level n is a quantum number.
- You might expect the waves on a given shell to be specified by two
quantum numbers, like positions on the Earth are specified by two
coordinates latitude and longitude, and stars on the sky by
declination and right ascension. Since we have used the letter
n for the radial quantum number, we will use the letters
l and m for the two angular quantum numbers.
- The quantum number l is roughly equivalent to a polar
angle coordinate like latitude and declination or elevation.
It counts the number of waves from "pole" to "pole" of the
shell.
- The quantum number m is similarly equivalent to an
azimuthal angle coordinate like longitude, right ascension, or
azimuth. It counts the number of waves around the "equator"
of the shell.
- Note that when we put our waves onto the sphere, they no longer
become sinusoids with n wavelengths around a circle. Since
they have to match up around all directions on the sphere, they
take on the properties of special functions called spherical
harmonics. They can have differing numbers of waves in the
two angular directions on the sphere - which is how we can tell them
apart, and why there are n^2 different ones!
- For a given level n, the quantum number l can take
on integer values from 0, 1, up to (n-1). There are
thus n different ones of these.
- For a given value of l, there quantum number m
can take on integer values from -l, -l+1, ...,
0, 1, ..., up to +l. There are (2l+1) different
values for these.
- Thus, if you add it all up, there are n^2 different allowed
combinations for l and m.
- It turns out that in additon to the radial and angular quantum
numbers n,l,m. particles like electrons
and protons have their own internal quantum number s,
which stands for spin. In a crude sense, it is useful
to think of particles as little spinning tops, with an axis of
rotation. For electrons and protons, the quantum number
s can take on one of two values of +1/2 or -1/2. These
correspond to states with the spin pointing "downward" and the
spin pointing "upward" (or clockwise or counterclockwise rotation)
from some given point of view.
- If we take into account this extra electron quantum number, we see
we can actually fit twice as many electrons into a shell
as we could without it, and still tell them apart. Thus, there
are places for 2n^2 electrons in each level n.
- The requirement that we be able to "distinguish" two electrons,
and their wave-functions, from each other, thus requiring them
to be labeled by distinct series of quantum numbers, is known as
the Pauli Exclusion Principle. The upshot of this is
you can only put 0, 1, or 2 electrons in any given
n,l,m state, and if you put two, they
must have different orientations of s.
- We call each different value of l, for a given level
n, an electron orbital. The orbitals were
historically given designations of s, p, d, f, etc. for values
of l = 0, 1, 2, 3, etc. respectively. Thus, the orbital
n=1, l = 0 would be called "1s", n=3,
l = 2 is "3d", and so on.
- In quantum mechanics, the interpretation of the wave-function of
a particle is that it represents the probability of where the
particle can be found. Thus, the crests and troughs of the wave
represent places where is is likely that the particle is, while
the zero-points of the wave are places where the particle isn't.
In the quantum mechanical picture of the Universe, you can never
pinpoint exactly where a particle is - only give probabilities
as given by the wave-function of that particle.
- Thus, the l and m quantum numbers tell where on the
shell the electron wave is "localized".
- The s orbital (l=m=0) is a wave-function that is
uniformly spread over the shell. You can place only two electrons
in an s orbital, and they must have opposite spins s.
- The p orbital (l=1, m=-1,0,+1) is a single-wavelength
wavefunction, so the electron probability is concentrated at either
of two opposite ends. There are three different orientations, with
the electron location concentrated along the x, y, or z axis (any
three perpendicular directions). You can place up to 6 electrons in
p orbitals, though if you put two in the same m sub-orbital,
then they must be of opposite spins.
- The chemical properties of atoms are governed by the which
orbitals are occupied in the outermost shells of electrons
- the so called valence electrons, since these are the
least tightly bound and are available for sharing with other
atoms. The organization of the Periodic Table of Elements
is entirely along the lines of the electron orbitals. Two atomic
elements with their outermost electrons in similar orbitals (though
in different n shells) will have the same chemical properties.
Most of chemistry has its base in the physics of atomic structure!
 Prev Lecture ---
Prev Lecture ---
 Next Lecture ---
Next Lecture ---
 Astr12 Index ---
Astr12 Index ---
 Astr12 Home
Astr12 Home
smyers@nrao.edu
Steven T. Myers
 Atomic Spectra --- | ---
Radiative Transfer
Atomic Spectra --- | ---
Radiative Transfer

 Atomic Spectra --- | ---
Radiative Transfer
Atomic Spectra --- | ---
Radiative Transfer

 Reading:
Reading: 



 i/kT ]
i/kT ]
 mekT / h2 )
exp[ -
mekT / h2 )
exp[ - i/kT ]
i/kT ]
 n=2
gn
exp[ En - E1 / kT ]
n=2
gn
exp[ En - E1 / kT ]
 i/kT ]
i/kT ]
 i/kT ]
i/kT ]
 ( N2/N2 /
( 1 + NII/NI )
( N2/N2 /
( 1 + NII/NI )

 Prev Lecture ---
Prev Lecture ---
 Next Lecture ---
Next Lecture ---
 Astr12 Index ---
Astr12 Index ---
 Astr12 Home
Astr12 Home