Introduction --- | ---
Intensity
Introduction --- | ---
Intensity
Reading:
Chapter 8-1, 11 (ZG4)
Notes:
pages 3 - 8
 |
Key Question: | What are the main methods for distance determination? |
|---|---|---|
 |
Key Principle: | The Distance Modulus |
 |
Key Problem: | What is the magnitude system and why is it commonly used? |
Every square meter of the Earth's surface receives a certain amount of sunlight, depending of course upon the time of day and the season. Consider a meter-square solar panel, which will convert the sunlight into electrical energy. Alternatively, we could also consider a meter-square panel of black absorbing material that would turn the sunlight into heat. In any event, when oriented perpendicular to the direction toward the Sun, such a panel will intercept the maximum amount of radiant solar energy. This can be measured as power in Watts --- Joules per second. If we were free of the Earth's atmosphere and had an unobstructed view of the Sun at a distance of 1 AU, we would find that we would intercept a particular flux of energy (in Watts per square meter). This is called the solar constant, and has the value of 1370 W/m^2.
Inclining the panel will reduce the intercepted power by the projected area, or
)
where F is the solar constant, A the panel area, and
the angle to the perpendicular.
Notice that we could in principle collect all of the Sun's emitted energy by constructing a sphere of radius R= 1 AU enclosing the Sun. Such a sci-fi construction is known as a Dyson sphere and every square meter of its surface would receive a flux equal to the solar constant F. The area of the sphere is 4 Pi R^2, so the Sun must be emitting a power, or luminosity L, of
For F=1370 watts/m^2 and R=1 AU=1.5 × 10^11 m, we find that the solar luminosity
(1.5 × 1011 m)2 × (1370 W/m2)
= 4 × 1026 W.
Notice that this relation between flux and luminosity will hold for spheres of any radius
R2)
and so the flux falls off as the inverse square of the distance from the source, be it the Sun or a light bulb! For example, the solar flux at the orbit of Mars (R=1.524 AU) will be 0.43 times the solar constant at 1 AU.
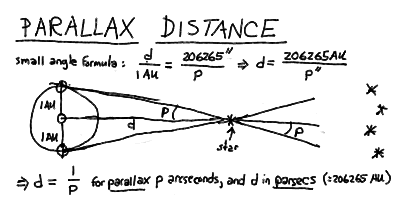
Finding distances using parallax:
Flux (brightness) and luminosity:
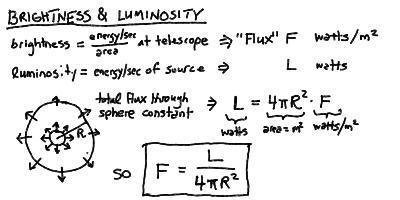
Absolute magnitudes and distance modulus:
The absolute visual magnitude of the Sun:
Luminosity and absolute visual magnitude:
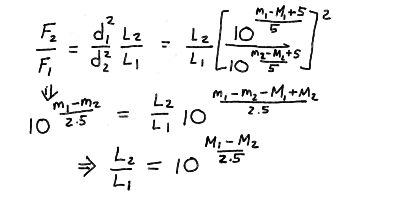
Calibrating the relation using the Sun:
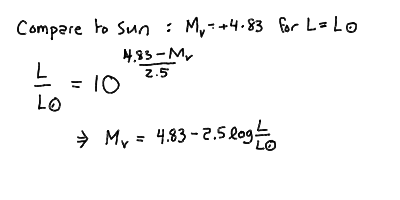
The Greek astronomer Hipparchus first systematized the visible stars by placing them in six classes ("first class", "second class", etc). This grew into the magnitude system for apparent brightness. Over the 6 magnitude classes that roughly cover the visible stars, the intensity varies by a factor of around 250. This gives rise to the peculiar system where 2.5 magnitudes equals a factor of 10 in brightness, and that larger magnitudes mean fainter stars. This is a logarithmic scale where
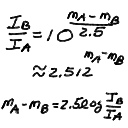
gives the relation between the intensities I_A and I_B for two objects A and B with apparent magnitudes m_A and m_B.
Here are the apparent visual magnitudes for some representative astronomical objects:
| Object | Apparent Magnitude |
|---|---|
| Sun | -26.5 |
| Full Moon | -12.5 |
| Venus (at brightest) | -4.4 |
| Mars (at brightest) | -2.7 |
| Jupiter (at brightest) | -2.6 |
| Sirius (brightest star) | -1.4 |
| Canopus (second brightest star) | -0.7 |
| Vega (zero of scale) | 0.0 |
| Spica | 1.0 |
| Naked-eye limit (urban areas) | 3 - 4 |
| Uranus | 5.5 |
| Naked-eye limit (rural areas) | 6 - 6.5 |
| Bright Asteroid | 6 |
| Neptune | 7.8 |
| Limit for typical binoculars | 9 - 10 |
| Limit for 15cm (6in) telescope | 13 |
| Pluto | 15 |
| Hubble Deep Survey | 30 |
Prev Lecture ---
Next Lecture ---
Astr12 Index ---
Astr12 Home
smyers@nrao.edu Steven T. Myers