Light --- | ---
Mechanics
Light --- | ---
Mechanics
Reading:
Chapter 8-1, 8-6 (ZG4)
Notes:
pages 8 - 12
 |
Key Question: | What is the difference between flux and intensity? |
|---|---|---|
 |
Key Principle: | Blackbody Radiation |
 |
Key Problem: | Calculate the surface flux from a blackbody at temperature T. |
It is well-known that if you heat stuff up, it glows! If you turn the burner on your electric stove to high, it starts to glow red. A flame is bright, and burning coals glow red. If you've ever seen iron or steel being heated in a furnace, you know that as you heat it to higher and higher temperatures it glows red, yellow, bluish, then white-hot, and at the same time brighter and brighter.
There is obviously a connection with temperature and light emission. The hotter something is, the brighter it glows, and the "bluer" a color the light that it emits is.
The temperature of a body is a measure of how fast the atoms and molecules in it are jiggling about. Higher temperature means higher average velocity (actually, average squared-velocity). In physics, the temperature is measured using a scale called the Kelvin scale (K). This is the same degrees in the centigrade or Celsius scale (C) (a change of 1 K = 1 C), but measured from absolute zero (zero velocity, 0 K = -273 C = -460 F) instead of from the freezing of water ( 0 Celsius = 273 Kelvin = 32 F). Thus, water boils at 373 K (100 C = 212 F).
The kinetic energy of a particle is proportional to the square of the velocity:
If you as what the distribution of kinetic energies of atoms in a gas at a temperature T is, you find a distribution that has is peaked at a characteristic kinetic energy, with few atoms at low energies (velocities), and few atoms at high energies (velocities). The average kinetic energy (we denote an average some quantity X by < X >):
where k is Boltzmann's constant (k=8.6 x 10^-5 eV/K).
Because the electric force is transmitted by photons, then it turns out that whenever you apply a force to an electron, and it is accelerated, it will emit a photon. The fact that accelerating electrons always emit radiation is an important one in astonomy, and we will return to it more than once. At this point, it is important in that collisions between atoms can cause the electrons in the outer shells to accelerate, and thus emit radiation. The spectrum of this "thermal" radiation depends on the thermal distribution of velocities and thus kinetic energies of the atoms in the material.
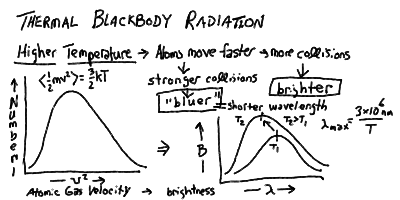
If a material is opaque, that is if nearly all the photons emitted by an atom inside the matter will be absorbed and re-emitted by other atoms in the substance before escaping out through the surface, then the energy of the radiation will come to equilibrium with the energy in the thermal motions of the agitated electrons. Thus, opaque matter at a temperature T (in Kelvin) radiates a continuous spectrum, whose peak shift to shorter wavelength and total energy rise with the temperature:
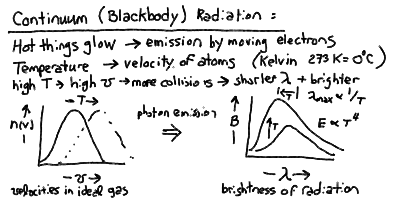
The peak wavelength of the blackbody radiation is inversely proportional to the temperature, and the total power radiated per square meter of surface is proportional to the fourth power of the temperature:
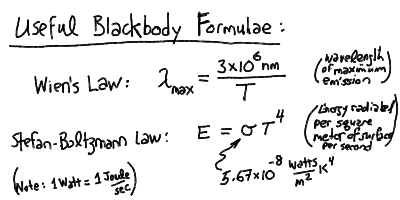
Thus, we can relate the observed spectra and radiative fluxes to the temperature of a blackbody. Most objects (stars, planets, etc) have an approximately blackbody spectrum. Therefore, this is one of the most important concepts in astrophysics.
An example of the use of thermal equilibrium with blackbody radiation is the radiation from our own bodies at approximately 300 K!
First we calculate the surface flux of blackbody radiation:
T4
= 5.67 x 10-8 · ( 300 )4
= 459 W m-2
It appears we light up like a bunch of 100 Watt light bulbs! Actually, we are in near thermal equilibrium with our surroundings, except for our internal heat (only 50 W or so); our body regulates the heat flow with our thermal surroundings.
We can calculate the wavelength of the peak blackbody emission using Wien's Law:
max 2.898 x 10-3 m /
(T/1K) 
3 x 10-3 m / 300
= 10-5 m = 10 µm
and lies in the mid-infrared (IR) part of the spectrum. This is why infrared goggles or infrared sensitive film can see a warm human body against a cold background in the dark!
Finally, we calculate the rms velocity of gas molecules in our lungs and around our bodies:
The gas molecules are zipping around at over 500 m/s, even though the typical bulk wind speed is only 1 m/s! However, this is all in equilibrium with the atmosphere around us.
Prev Lecture ---
Next Lecture ---
Astr12 Index ---
Astr12 Home
smyers@nrao.edu Steven T. Myers