


Reading:
Chapter 11 (ZG4)
Notes:
pages 1 - 3
 |
Key Question: | How do we find out about the distant Universe? |
|---|---|---|
 |
Key Principle: | The Electromagnetic Spectrum |
 |
Key Problem: | What does light tell us about where it came from? |
No worries. I mostly talked about the stuff in the course guide, and some of the topics listed above. Oh, and I showed some cool laserdisk pictures too. You can find photocopies of my lecture notes on reserve in the Physics, Math & Astronomy Library, 3rd Floor, North Wing, DRL.
The notes summarized below give extra explanations for some of the key concepts from this lecture:
The electromagnetic wave, as described by Maxwell's equations, consists of mutually perpendicular harmonic electric and magnetic fields oscillating in phase and propagating in the orthogonal direction.
Almost everything we know about the Universe has been brought to us by the light that we observe with our instruments and eyes. Light, radio waves, radar, X-rays and ultraviolet rays are all examples of the same phenomenon of electromagnetic radiation. Light can be thought of as a electromagnetic wave with crests and troughs as in ocean waves (but without the ocean!). The things that are rising and falling in an electromagnetic wave are the electric and magnetic "fields", which rise and fall in step as a function of space and time. If we were to freeze time, and move along the direction of a wave, we would measure electric and magnetic forces that increased then decreased then changed direction and back again, like a sine wave. The distance between crests of the wave is called the wavelength and is measured in meters (or centimeters or nanometers, whatever is convenient). If one were to let time move normally, but measure the electric and magnetic forces as a wave passes by, then we would see the crests and troughs moving past us at the speed of light. Thus, we would see the waves pass us at the frequency of a certain number of cycles per second, say f, given by:
f = c / l
where l is meant to be the wavelength. We are familiar in using frequency to describe radio waves. When we say our favorite radio station has a frequency of 100 Megacycles (or MegaHertz), we mean that f = 100 x 10^6, that is 10^8, cycles per second. (Remember, mega means 10^6). Note that since the speed of light c = 3 x 10^8 m/s, that a frequency of 100 megacycles corresponds to a wavelength l = c/f = 3 meters.
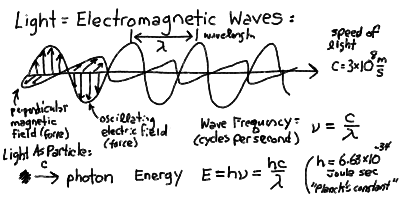
The electric and magnetic forces in an electromagnetic wave are at right angles (perpendicular) to each other always.
The electric and magnetic forces from an electromagnetic wave, such as visible light or radio waves, can be measured. A radio wave, with a wavelength of 1 meter for example, can cause electrons in a wire of about that same length to move back and forth due to the oscillating electric force in the wave. These moving electrons are measureable as an electric current in the wire - this is how a radio or TV antenna works to receive signals!
The electrons in the metal of the antenna (which is basically just a long wire) are free to move a little in response to the radio wave electric field. The current alternates like a sine wave. The reverse is also true! If you oscillate the current like a sine wave in a long wire, an electromagnetic wave of the same frequency is generated. This is how radio and TV transmitters work.
Light can also be thought of as made up of particles, known as photons. Light is both a wave and a particle at the same time. The reconciliation of this dual nature has been one of the greatest breakthroughs in physics at the turn of the century. Each photon has a specific energy given proportional to the frequency of the wave that it corresponds to. The energy of a photon of frequency f is:
E = h f
where the constant h is known as Planck's constant. Planck's constant h = 6.63 × 10^-34 Joules sec.
There are many different energy photons, with energies ranging from zero to infinity, each corresponding to waves with wavelengths from infintely long to infintesimally small (zero). This is what is called the electromagnetic spectrum Radio waves, with wavelengths around 1 meter, are fundamentally the same as visible light, with wavelength around 500 nanometers (nm), the same as X-rays, with wavelengths around 1 nm. Because the photon energy is proportional to frequency, the high frequency, short wavelength radiation like UV and X-rays and Gamma Rays can actually do major damage to our bodies if we are exposed to it. It takes many microwaves (wavelength about 1 cm) to cook food in a microwave oven, because the photons each have very low energy. Nuclear explosions release large amounts of deadly Gamma Rays, each of which can do lots of molecular damage when they pass into organic material.
Different materials absorb specific frequencies of light. This is due to resonances with atomic and molecular structures as we will see later on. The air in the Earth's atmosphere absorbs the waves except special "windows" or wavelength bands where it is transparent. Both visible light and radio waves fall in these windows, so we can see out from the Earth into the heavens.
The small angle formula tells us that the angle (in radians) subtended by an object of diameter D at distance r is:
 = D / r
= D / r This can be turned around in that if we observe an object shift direction by this angle (in radians) when we move a distance D perpendicular to its direction, then it must be at a distance r.
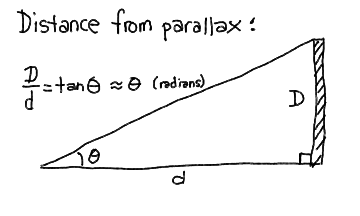
There are 206265 arcseconds (") in a radian, so the angular size of an object of diameter D at distance r is
 " = 206265 * D / r
" = 206265 * D / r If we use the baseline of the Earth's orbit (2 AU for 6 months apart) and see a shift of theta = 2 * p arcseconds, then
It is customary to define p as the parallax. Thus a parallax p of 1" means that the distance r is 206265 AU. If we define the unit of distance called the parsec to be 1 pc = 206265 AU, then
A star 1 parsec away has a parallax of 1 arcsecond. Talk about convenience! Note that 1 pc is about 3.26 light-years. The nearest star is around 1 pc away.
 Next Lecture ---
Next Lecture ---
 Astr12 Index ---
Astr12 Index ---
 Astr12 Home
Astr12 Home
smyers@nrao.edu Steven T. Myers