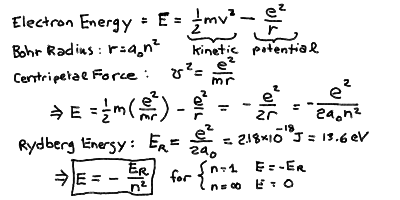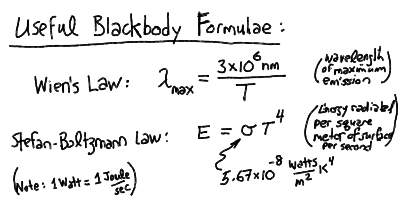Lecture 20 - Atomic Spectra (2/28/96)
Seeds: Chapter 6
- The Bohr Atom: Orbital Radii and
Energy Levels
- For an electron wave not to interfere with itself, there must
be an integer number n wavelengths on an orbit. The
smallest allowed orbit contains a single wavelength.
- The radius of the orbit is: r = (h/2Pi)^2 ( n^2 / m e^2)
- The radius for n = 1 is the Bohr radius:
a_0 = h^2 / ( 4 Pi^2 m e^2)
- Then, r = a_0 n^2
- The energy of a moving particle under a force is:
E = (m v^2 / 2) - (e^2 / r)
- The first term (m v^2/ 2) is the kinetic energy, and
the second term (-e^2/r) is the potential energy.
- Using the Coulomb and centripetal forces, we find:
E = - e^2/2r = -e^2 / (2 a_0 n^2)
- Thus, E = - E_R / n^2 where E_R = e^2 / (2 a_0) is
the Rydberg Energy for hydrogen.
- Thus, the energy levels are spaced like the inverse square of the
level number n, while the radii are spaced like the square
of n.
- From all the constants you can compute the values of the Bohr Radius
a_0 = 5.29 x 10^-11 m = 0.053 nm, and the Rydberg energy
E_R = 2.18 x 10^-18 Joules = 13.6 eV.
- We define the the electron volt (eV) as
the energy gained by an electron accelerated through a voltage
difference of 1 volt (like from a battery).
1eV = 1.602 x 10^-19 J
- An electron at rest infinitely far away from the proton
(n = infinity) has E = 0, while the ground state
n = 1 has an energy E = -13.6 eV.
- It takes an energy of 13.6 eV to remove an electron in the
ground state from the hydrogen atom (ionization, see below).
- Hydrogen Energy Levels and Line Series
- Now that we have the energy levels of hydrogen, we can compute
easily the wavelengths of light emitted and absorbed on
transitions between different orbits.
- These are called spectral lines because in the spectrum
of a star (the brightness versus frequency) these show up as narrow
"lines" at specific wavelengths.
- The energy of a photon of wavelength L is just E = h c / L.
The energy difference between a lower level m and an
upper level n > m is just
(E_n - E_m) = E_R ( 1/m^2 - 1/n^2)
- Thus, the wavelength L corresponding to this difference is given by:
(h c / E_R) / L = 1/m^2 - 1/n^2
- If we define the Rydberg wavelength L_R = (h c / E_R) = 91.18 nm,
then:
L_R / L = 1/m^2 - 1/n^2
- We see immediately that the largest energy transition is from
the ground state m=1 to n=infinity (13.6 eV) has
a wavelength of 91.18 nm. Photons of this wavelength or shorter
will remove the electron from hydrogen entirely (see Ionization
below). All other hydrogen lines have wavelengths longer than this.
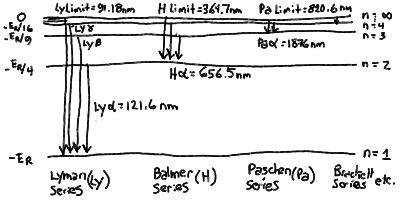
- There are series of lines corresponding to transitions between
each lower level m and all upper levels. The series for
the ground state m=1 and all higher levels is called the
Lyman Series. The longest Lyman line corresponds to an
upper level n=2, and from our formula can be seen to have
a wavelength of 121.6 nm. All the other Lyman lines have wavelength
between this and the Lyman limit of 91.18 nm.
- These series of lines have a charateristic spacing that converge
closer and closer to the limit for n=infinity.
- The longest wavelength line in a given series is designated by
the Greek letter Alpha. The next is Beta, then Gamma, then Delta,
and so on. The Lyman series is thus Ly Alpha (121.6 nm), Ly Beta
(102.6 nm), Ly Gamma (97.25 nm), and so on. We abbreviate Lyman
as Ly.
- From those wavelengths, you can see that the Lyman line series
is hard to see since it is in the ultraviolet part of the spectrum
which is absorbed by the Earth's atmosphere. It is much easier to
see the next series corresponding to a lower level m=2.
- The Balmer Series is between a lower level m=2 and
those above. The first line is H Alpha (the designation for Balmer
for historical reasons is H for Hydrogen) at 656.6 nm, with
H Beta (486.3 nm), H Gamma (434.3 nm), H Delta (410.3 nm) and so
on up to the Balmer limit of 364.7 nm.
- The Balmer lines are in the visible part of the spectrum and are
prominent in most stars.
- There are other series of lines, Paschen for m=3
( Pa Alpha = 1876 nm, limit = 820.6 nm) and Brackett for
m=4 ( Br Alpha = 4052 nm, limit = 1459 nm ). These
lines are in the infrared part of the spectrum and harder
to measure from the ground.
- As is common in this subject, astronomers are not content to use
normal units for wavelength like nanometers. They use the
Angstrom (A) which is just one-tenth of a nm, or
1 A = 10^-10 m, and so 10 A = 1 nm.
Thus, the wavelength of H Alpha is 6565 A, Ly Alpha is 1216 A,
and the Lyman limit is 912 A.
- The Bohr radius a_0 is 0.529 A. Most atoms are a few Angstroms
across.
- We will continue to use nm to measure wavelength.
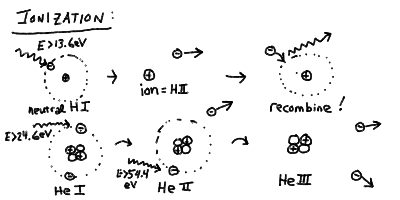
- Ionization
- If a photon of short enough wavelength (high energy) is absorbed,
for example shorter than 91.18 nm for hydrogen, then the electron
is knocked clear out of the atom, and it is free to roam the universe
at will.
- This process is called ionization and can also be caused by
a strong enough collision. Ionization leaves behind a free electron,
and an atom that is now positively charged - and is called an
ion.
- The free electron can later (actually not very much later ususally)
recombine with this or another ion, since it is attracted by
the electric force.
- In multi-electron atoms, such as any other type of atom than
hydrogen, it takes more energy to knock out successive electrons
after you remove the first one. This is just because there is
more charge pulling on fewer electrons (which tend to screen each
other from the nucleus).
- Also, it takes more energy to remove electrons that are closer to
the nucleus, since they have a more negative energy E. It is always
the outermost, or the least tightly bound, electron that is first
removed upon ionization.
- Ionization states of atoms are designated by the chemical symbol
for the element (H=hydrogen, He=Helium, C=Carbon, etc) and a
Roman numeral (I=neutral, II=singly ionized, III=doubly ionized, etc.)
- Thus neutral hydrogen is H I, and ionized hydrogen (a proton and an
electron) is H II.
- Neutral Helium is He I, singly ionized Helium is He II (one electron
removed), and doubly ionized Helium is He III.
- It takes 13.6 eV to turn H I into H II. It takes 24.6 eV to turn
He I into He II, and another 54.4 eV to turn He II into He III.
The ionization energy of He 24.6 eV is slightly less than twice
hydrogen because of the screening of the other electron. The
ionization energy from He II to He III is four times 13.6 eV
because the energy goes as the charge squared, and He II looks like
hydrogen with a single electron, but more positive charge in the
nucleus.
- Electron Orbitals and Quantum Numbers
- We have established orbits, or electron shells, with
increasing radius from the nucleus
r = a_0 n^2
and increasing energy
E = -E_R / n^2
In some sense, we have labeled these orbits or states by
the magic number n, which increased from the ground
state n = 1.
- A good question was asked in class - we have been drawing the electron
orbit as a circle, like a planet's orbit. But atoms are spherical.
Should we take that into account?
- The answer to that is yes - in fact, it is crucial for the structure
of atoms and how atoms interact with each other. If orbits were
circular, then we can see that we can only put one electron on
a given shell without it interfering. It turns out if you compute
the number of separate waves that you can put on a spherical
shell at level n, you find that you can actually put
n^2 waves and still be able to tell them apart! (This is
like the surface area of the sphere goes like the radius squared.)
Thus, you can put more than one electron into each shell, as long
as you can tell them apart.
- The way you tell apart two electrons is by labeling them by a series
of quantum numbers, like we tell apart houses by addresses.
The level n is a quantum number.
- You might expect the waves on a given shell to be specified by two
quantum numbers, like positions on the Earth are specified by two
coordinates latitude and longitude, and stars on the sky by
declination and right ascension. Since we have used the letter
n for the radial quantum number, we will use the letters
l and m for the two angular quantum numbers.
The quantum number l is roughly equivalent to a polar
angle coordinate like latitude and declination or elevation.
It counts the number of waves from "pole" to "pole" of the
shell.
The quantum number m is similarly equivalent to an
azimuthal angle coordinate like longitude, right ascension, or
azimuth. It counts the number of waves around the "equator"
of the shell.
- Note that when we put our waves onto the sphere, they no longer
become sinusoids with n wavelengths around a circle. Since
they have to match up around all directions on the sphere, they
take on the properties of special functions called spherical
harmonics. They can have differing numbers of waves in the
two angular directions on the sphere - which is how we can tell them
apart, and why there are n^2 different ones!
- For a given level n, the quantum number l can take
on integer values from 0, 1, up to (n-1). There are
thus n different ones of these.
For a given value of l, there quantum number m
can take on integer values from -l, -l+1, ...,
0, 1, ..., up to +l. There are (2l+1) different
values for these.
Thus, if you add it all up, there are n^2 different allowed
combinations for l and m.
- It turns out that in additon to the radial and angular quantum
numbers n,l,m. particles like electrons
and protons have their own internal quantum number s,
which stands for spin. In a crude sense, it is useful
to think of particles as little spinning tops, with an axis of
rotation. For electrons and protons, the quantum number
s can take on one of two values of +1/2 or -1/2. These
correspond to states with the spin pointing "downward" and the
spin pointing "upward" (or clockwise or counterclockwise rotation)
from some given point of view.
- If we take into account this extra electron quantum number, we see
we can actually fit twice as many electrons into a shell
as we could without it, and still tell them apart. Thus, there
are places for 2n^2 electrons in each level n.
- The requirement that we be able to "distinguish" two electrons,
and their wave-functions, from each other, thus requiring them
to be labeled by distinct series of quantum numbers, is known as
the Pauli Exclusion Principle. The upshot of this is
you can only put 0, 1, or 2 electrons in any given
n,l,m state, and if you put two, they
must have different orientations of s.
- We call each different value of l, for a given level
n, an electron orbital. The orbitals were
historically given designations of s, p, d, f, etc. for values
of l = 0, 1, 2, 3, etc. respectively. Thus, the orbital
n=1, l = 0 would be called "1s", n=3,
l = 2 is "3d", and so on.
- In quantum mechanics, the interpretation of the wave-function of
a particle is that it represents the probability of where the
particle can be found. Thus, the crests and troughs of the wave
represent places where is is likely that the particle is, while
the zero-points of the wave are places where the particle isn't.
In the quantum mechanical picture of the Universe, you can never
pinpoint exactly where a particle is - only give probabilities
as given by the wave-function of that particle.
- Thus, the l and m quantum numbers tell where on the
shell the electron wave is "localized".
The s orbital (l=m=0) is a wave-function that is
uniformly spread over the shell. You can place only two electrons
in an s orbital, and they must have opposite spins s.
The p orbital (l=1, m=-1,0,+1) is a single-wavelength
wavefunction, so the electron probability is concentrated at either
of two opposite ends. There are three different orientations, with
the electron location concentrated along the x, y, or z axis (any
three perpendicular directions). You can place up to 6 electrons in
p orbitals, though if you put two in the same m sub-orbital,
then they must be of opposite spins.
- The chemical properties of atoms are governed by the which
orbitals are occupied in the outermost shells of electrons
- the so called valence electrons, since these are the
least tightly bound and are available for sharing with other
atoms. The organization of the Periodic Table of Elements
is entirely along the lines of the electron orbitals. Two atomic
elements with their outermost electrons in similar orbitals (though
in different n shells) will have the same chemical properties.
Most of chemistry has its base in the physics of atomic structure!
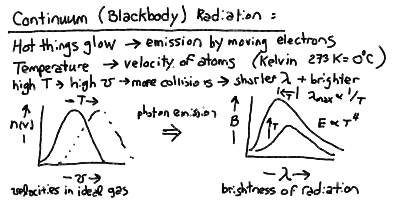
- Thermal Blackbody Radiation
- If you heat stuff up, it glows and emits light. The hotter
you make it, the brighter it gets, and the bluer in color
it gets until it is "white hot" (which is of course hotter
then "red hot"). This phenomenon is called thermal radiation.
- Thermal radiation is also called blackbody radiation because
it is most easily calculated for a "black" substance that absorbs
all light that falls on it (and also emits back the same light but
in thermal equilibrium, and thus possibly at a different wavelength
as we will see). Any opaque material will emit thermal blackbody
radiation - that is photons with the characteristic thermal
distribution.
- The thermal spectrum of photons is continuous, a smooth
function of wavelength, in contrast to the spiky line emission at
the discrete energy levels of atoms.
- The thermal spectrum is a maximum (brightest) at a characteristic
wavelength L_max inversely proportional to the temperature:
L_max = 3 x 10^6 nm / T
where the temperature T is measured in degrees Kelvin.
- The total energy emitted in thermal radiation per square meter
of surface of the body is proportional to the fourth power
of the temperature:
E = S T^4
where S is a constant (see next lecture).
- We will continue our discussion of thermal radiation in more
detail next lecture.
Next Lecture - Spectral Classes
of Stars
The Bohr Atom: Orbital Radii and Energy Levels
As we saw last time, the condition that an electron wave not interfere with
itself on an orbit means that there must be an integer number, say n,
wavelengths on an orbit. The smallest allowed orbit contains a single
wavelength. We wish to compute the radius and Energy of the orbits in the
hydrogen atom. This was done by Niels Bohr. This gives the relation that
2 Pi r = n L_e
where L_e is the wavelength of the electron and r is the orbital
radius.
From the physicist de Broglie, we know that the wavelength of
an electron is proportional to the inverse of its
momentum:
L_e = h / m v,
where m is the electron mass and v is the velocity
of the electron, and h is Planck's constant.
Thus, we find the velocity of the electron to be given by:
v = (h/2Pi) (n/ m r)
Just like when we wanted to derive Kepler's law from the gravitational
force we used the centripetal acceleration to give us the velocity,
we do the same here. We have the Coulomb force
F = e^2/r^2
where we have absorbed the constant into the units for the electron and
proton charges +e and -e.
The centripetal force is just F = m v^2 / r, so we equate
( e^2 / r^2 ) = (m v^2 / r)
and thus we find:
v^2 r = e^2 / m
Substituting in our expression for the velocity in the above equation
gives
( (h/2pi)( n/mr) )^2 r = (e^2 / m)
and so we get:
r = (h/2Pi)^2 ( n^2 / m e^2)
If we define the radius for n = 1 to be the Bohr radius:
a_0 = h^2 / ( 4 Pi^2 m e^2),
then we find the simple relation for the orbital radius:
r = a_0 n^2
The orbital radii of the hydrogen atom, quantised by the number
of wavelengths n:

To find the energy levels, we need to know what the energy of a
moving particle under a force is. It turns out it has two terms
due to the motion and due to the force:
E = (m v^2 / 2) - (e^2 / r)
The first term (m v^2/ 2) is called the kinetic energy and
is the energy carried in the motion of the electron, like the energy
in a thrown baseball which you feel when it hits you.
The second term (-e^2/r) is called the potential energy, and
it is the energy "contained" in the electric force that you must
work with or against to move an electron closer or farther from the
nucleus. It has the opposite sign to the kinetic energy because
the total energy is conserved, you cant make or destroy energy
out of nothing. Thus if you speed up an electron (increase its
kinetic energy) you must draw it from the potential
energy due to the electric force (decrease its potential energy).
If we compute the energy E, we see that since v^2 r = e^2 / m
from the centripetal force, then L
E = - e^2/2r
Substituting in r = a_0, then easily we find:
E = -e^2 / (2 a_0 n^2)
If we define the energy at the ground state n=1 to be
E_R = e^2 / (2 a_0),
the Rydberg Energy for hydrogen, then
E = - E_R / n^2
Thus, the energy levels are spaced like the inverse square of the
level number n, while the radii are spaced like the square
of n.
The energy levels of the hydrogen atom:
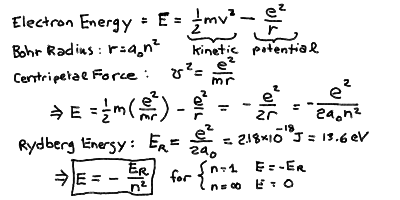
From all the constants you can compute the values of the Bohr Radius
a_0 = 5.29 x 10^-11 m = 0.053 nm, and the Rydberg energy
E_R = 2.18 x 10^-18 Joules = 13.6 eV.
We have defined a more convenient unit of energy: the electron volt
(eV). This is the energy gained by an electron accelerated through a voltage
difference of 1 volt (like from a battery). Its very tiny
( 1eV = 1.602 x 10^-19 J ).
In this energy level scheme, we see that an electron at rest infintely
far away from the proton (in the absence of any other atoms!) has
an energy of E = 0 (for n = infinity). The ground state
n = 1 has an energy E = -13.6 eV. Thus, it takes an energy
of 13.6 eV to remove an electron in the ground state from the hydrogen
atom.
Hydrogen Energy Levels and Line Series
The Rydberg formula for the transition wavelengths between two
energy levels m and n in hydrogen:

The line series of hydrogen corresponding to transitions between
upper levels and lower levels:
Ionization
The process of ionization and recombination and the ionization states
of hydrogen and helium:
Electron Orbitals and Quantum Numbers
The quantum numbers of electrons in the atom:

The configuration of electrons in the different l orbitals:

Continuum Emission and Blackbody Radiation
Opaque matter at a temperature T (in Kelvin) radiates a continuous spectrum
of light caused by the movement and collisions of atoms (and their electrons)
The peak wavelength of the blackbody radiation is inversely proportional
to the temperature, and the total power radiated per square meter of surface
is proportional to the fourth power of the temperature:
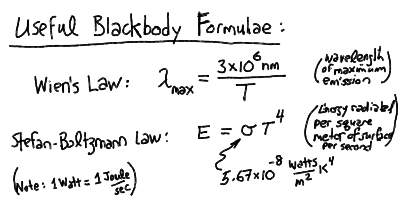
Go to Previous Lecture ----
Go to Next Lecture
Back to the Lecture Notes Index
Back to the ASTR001/Sec3 Page
Steven T. Myers - Last revised 01Mar96