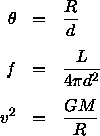
There are 3 "observable" physical properties of galaxies, R, L, and M, as there are in stars. These are given by the relations
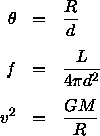
The distance d enters into the small-angle relation and the flux-luminosity relation. We can eliminate this between the two using the surface brightness
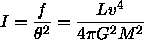
which is independent of the distance, as we discussed in Lecture 3. We can rearrange this to find
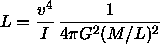
where we have introduced the mass-to-light ratio M/L. If we can assume that for a given class of galaxies that the central surface brightness I (in Lsun/pc^2) and the mass-to-light ratio M/L are constant, then we find the relation
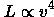
which is the basis of some of the most useful distance indicators in cosmology! For instance, if we are observing spiral galaxies, the appropriate velocity to use is the maximum velocity v_max in the rotation curve which can be determined from H I spectra. Then, we have
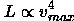
which is known as the Tully-Fisher relation. On the other hand, if we are concerned with elliptical galaxies, the appropriate velocity is the central velocity dispersion
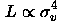
which is known as the Faber-Jackson relation. Both of these relations were discovered empirically and are justified through the arguments given above. The proportionality must be calibrated using galaxies with known distances, then the relations can be used to find the luminosity, and thus the distance, given an observation of the apparent magnitude and velocity width. For example, a typical relation for ellipticals is
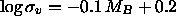
where MB is the absolute galaxy magnitude (to some isophotal level) in the B band.
Note that it is still under debate whether these relations are universal, that is, whether I and M/L are dependent only on the galaxy type, and do not depend on other things such as location and environment.
 Astro12 Index ---
Astro12 Index ---
 Astro12 Home
Astro12 Home
smyers@nrao.edu Steven T. Myers