The bolometric luminosity is given by
R2 ·
T4 =
8.05 x 1017 W = 2.10 x 10-9
L
while Wien's Law gives
max = 2.898mm / 122 =
2.375 x 10-5 m = 23.75 µm
which is in the infrared. If we turn the luminosity ratio versus the Sun into a magnitude difference, we get
(note: this holds for both apparent and absolute magnitudes, since we will be considering distant systems that are equivalent to Jupiter and our Sun, not our own solar systme per se). So,
and thus if our limiting apparent magnitude were m = 30, we could detect the flux from Jupiter at a maximum distance modulus of
Thus, we could detect Jupiter if it were closer than 51 parsecs, and could certainly detect Jupiter at 10 parsecs (where m = M = +26.44 < 30).
An angular scale of 0.1" at distance d corresponds to a physical scale of R = 5.2 AU of
= (0.1"/206265") rad = 5.2 AU / (d / 1 AU)
= (5.2 AU/ 206265 AU) / (d / 1 pc) --> d = 5.2/0.1 = 52 pc
which we could have easily seen by noting that 1 AU = 1" at d=1 pc, so 1 AU = 0.1" at d=10 pc and therefore 5.2 AU = 0.1" at d=52 pc! Note that this limiting distance of 52 pc for the angular resolution of the binary is nearly the same as the 51.3 pc we got for the luminosity of Jupiter, but this is just a coincidence.
In an approximately circular orbit with semimajor axis a:
a / P =
( G M / a )1/2 = 13070 m/s
or 13.07 km/s. As for any orbital problem, we will apply Kepler's 3rd (harmonic) Law, which holds in the reduced mass relative orbit frame:
2 a3
--> M = 42a3 /
GP2 = Pv3 / 2G
where for the Sun (S) and Jupiter (J) masses
which allow us to switch to the center-of-mass and momentum frame, and give the velocities with respect to the barycenter
MS vS = MJ vJ
from the mass ratio. Thus, since
then
v >> vS -->
vS v (MJ/MS)
= 13070 / 1053 = 12.42 m/s.
If we can measure a stellar reflex velocity of v_s ~ 1 m/s, then what we are actually talking about is an equivalent relative (planetary) velocity of v = 1053 m/s, which tells us that the orbital radius is
from our above calculation. We can solve this for a assuming v = 1 m/s
Note that our current spectroscopic technology can only determine radial velocities to ~ 10 m/s at best, so we could find Jupiters at 8 AU which is only slightly farther than our own Jupiter (we could detect Saturn, for example).
If we consider an Earth-mass planet, where now the Sun-mass star is relatively more massive
then everything we did before just scales, and our v_S = 1 m/s now is equivalent to v = 3.34 x 105 m/s. This is found for an orbit with semimajor axis of
Note that this pathetically small orbit is only 1.7 Rsun and thus such a planet would be uninhabitable and hardly Earthlike. Radial velocities are an impractical method for finding Earth-mass planets around solar-type stars.
We have P and v known, so we trot out our warhorse Kepler's 3rd Law
2 a3
--> M = 42a3 /
GP2 = Pv3 / 2G
where once again it is assumed that we are talking about the relative orbit with reduced mass µ orbiting total mass M. The difference now is that we can only measure the radial component of the velocity (the Doppler effect is only sensitive to the velocity toward or away from us), with
where i is the inclination angle (i=90° is edge-on). Thus, substituting for v in the mass equation
G =
( P / 2G )
( vrad / sin i )3
and moving all the stuff we know to the right side, and putting the unknown stuff on the left, we find the mass function
G.
We can make things even simpler, noting that we can calibrate to the Earth's orbit around the solar-mass Sun, where v_E = 29.86 km/s with period P = 1 year
) =
( P / 1 year )( v / 29.86 km/s )3
(which will also hold for the radial components) and so for P = 1.67 days and total velocity v = 121.4 + 247 km/s = 368.4 km/s
=
( 1.67 d / 365.26 d )( 368.4 km/s / 29.86 km/s )3
= 8.59
and thus the mass function M sin^3i = 8.59 solar masses. The individual masses are obtained from the velocity ratio
and thus
sun =
3.035 M2
sin3i --> M2 sin3i =
2.83 M
and
.
Note that we are unable to remove the inclination factor, so even the individual masses are in the form of a mass function. However, since 0 < sin^3 i < 1, the mass function is a lower limit to the true mass.
Remember, all orbit problems are Kepler's 3rd Law problems!
In this case, we again know P and v, but we also know from the flat-bottomed
eclipses that the system is edge-on, with inclination i
90°, so sin^3 i
1.
Thus, the radial velocity is the total velocity and as before we use
G =
( M / M ) =
( P / 1 year )( v / 29.86 km/s )3 = ( 8 yrs / 1 yr )( 29.86 km/s / 29.86 km/s )3 = 8 M
!
Notice the benefit from scaling to the Earth's orbit. The primary of the system is Itchy ( = 1 ) and the secondary is Scratchy ( = 2 ). Since
--> 8 M
= 16 M2 --> M2 = 0.5 M
,
M1 = 7.5 M.
From the mass and the period (or period and velocity) we get the (total orbital) circular velocity
)
( 29.86 km/s / v )2 = 8 AU
where we again have scale to the Earth's orbit around the Sun, and used our observed v = 29.86 km/s and 8 Msun mass determination. Since we are told that this 8 AU orbital radius corresponds to 0.2", and we remember that the definition of the parsec tells us 1 AU at 1 pc = 1", we know 8 AU at 1 pc = 8", so 8 AU = 0.2" at 8/0.2 = 40 pc! If this is too confusing, we can compute it directly
= ( 0.2" / 206265" ) rad =
( 8 AU / 206265 AU/pc )( 1 pc / d ) --> d = 8 / 0.2 = 40 pc
as expected.
For the primary, m = -0.5 at d = 40pc, so the distance modulus gives
and since M = +4.75 for the Sun,
and thus Itchy has a luminosity of nearly 2000 Lsun! This may seem high, but examination of the H-R diagram in the textbook shows that upper main sequence stars (type O) can have luminosities greater than 10^4 Lsun. The secondary scratchy has m = 10.4, and thus is
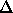m = -0.5 - 10.4 = -10.9 =
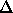M --> M = -3.5 + 10.9 = +7.4
and is 10.9 magnitudes fainter than Itchy, so it will have a luminosity
.
With these luminosities, we can then compute the radii using the blackbody surface flux times the surface area:
=
( L / L )1/2
( T / T )2
Finally, with T_1 = 18700 K and T_2 = 3850 K (vs. T_sun = 5770 K) we compute
R2 = ( 0.087 )1/2 ( 5770 / 3850 )2 = 0.66 R
and thus Itchy (7.5Msun, 2000 Lsun, 4.25Rsun) and Scratchy (0.5Msun, 0.087Lsun, 0.66Rsun) see to be run of the mill main sequency stars. (Q: Do these stars follow the expected mass-luminosity relation for main sequence stars? What spectral types are they?)
You should have found from problem set 1 the values
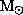L = 23.3 
Sirius B: M = 1.05
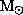L = 0.0296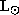
to which we now add the spectral temperatures
Sirius B: M = 27000 K
versus the Sun's temperature of 5770 K. We compute the radii, using the same procedure as in the previous problem,
Sirius B: R = ( 0.0296 )1/2 ( 5770 / 27000 )2 = 0.0079 R
!
Note that the radius of the Sun is 6.96 x 10^5 km, so the radius of Sirius B is 5469 km, or 0.86 times the radius of the Earth. There is a solar mass of material packed into a star the size of the Earth!
The average densities are given by the ratios of the mass to the volume of the sphere
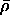= 3M /
( 4R3 ) =
1416 ( M / M )
( R / R )-3
kg m-3
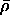= 1416 ( 2.25 )
( 1.90 )-3 = 465 kg m-3
Sirius B:
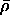= 1416 ( 1.05 )
( 0.0079 )-3 = 3.0 x 109 kg m-3 !
The mean density of Sirius B is over 3 million metric tons per cubic meter, or equivalently 3 tons per cubic centimeter! Sirius B is an example of a white dwarf star.