Wien's Law gives
max = 2.898mm / 5770
= 5.02 x 10-7 m = 5020 Å
or in frequency
max =
c/max =
5.97 x 1014 Hz
Note that the Boltzmann factor is
/kT = 4.97
at the blackbody maximum, so we cannot use either the Rayleigh-Jeans or Wien approximations for x<<1 or x>>1 respectively! The full blackbody intensity expression gives
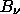(max) =
2h3/c2
[ ex - 1 ] = 2.20 x 10-8 W/m2/Hz/sr
for our Boltzmann factor x, and thus the flux density at the blackbody maximum is
= 
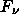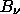= 6.91 x 10-8 W/m2/Hz
and
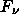= 4.13 x 107 W/m2.
We compare this to the fully correct Stefan-Boltzmann surface flux from the Sun of
T4
= 6.28 x 107 W/m2
which if we multiply by the Sun's surface area gives the Solar Luminosity. Thus, our approximation of nu*Fnu as the flux is not too bad!
The relevant triangle (arc) has R_J subtending angle theta at distance d = 4.2 AU = 6.28 x 10^8 km:
= RJ / d = 1.14 x
10-4 rad --> (1.14 x 10-4 rad)(206265 "/rad)
= 23.4"
and so Jupiter has an apparent angular radius of 23.4 arcseconds (or angular diameter of 46.8"). The solid angle is just the ANGULAR AREA of the disk of Jupiter, which for small angles is given by the usual Cartesian formula for the area of a flat circular disk
=
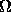2 = 4.06 x 10-8 sr
since steradians are just square radians!
At 30GHz or 3 x 10^10 Hz, and T = 122 K the Boltzmann factor is
/kT = 0.0118
and indeed x << 1, so we can use the Rayleigh-Jeans approximation to the Blackbody function
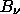
2kT2/
c2 = 2kT/2 =
3.37 x 10-17 W/m2/Hz/sr
or since 1 Jy = 10^-26 W/m^2/Hz
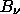= 3.37 x 109 Jy/sr.
For our solid angle of 4.06 x 10^-8 sr determined above, the flux density from Jupiter at this wavelength is
=
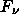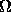
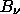= 1.367 x 10-24 W/m2/Hz
= 136.7 Jy.
To estimate the flux, we again multiply by the frequency 3 x 10^10 Hz
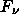= 4.1 x 10-14 W/m2.
The collecting area of a telescope of radius R = 5 meters is
R^2 = 78.54 m2
so
is the power collected. Note that this is even a million times smaller than a microwatt! This is why radio astronomers have to use huge antennas (with diamters up to 300 meters!), high-gain low-noise amplifiers, and cryogenic receivers to detect the faint signals from astronomical sources.
For parallax p = 0.377", the distance (at which 1 AU corresponds to the parallax) is
and therefore the distance modulus is
so
which in comparison to the Sun (M=+4.75) means
for Sirius A. Since the distance modulus is the same for A and B, The apparent magnitude m = +5.69 corresponds to absolute magnitude
and
for Sirius B. Thus,
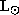Sirius-B: L = 0.0296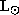
are the luminosities of the individual components in solar units.
The parallax of 0.377" implies that at the distance of Sirius, 1 AU subtends an angle of 0.377", and thus 7.62" corresponds to 7.62/0.377 = 20.2 AU! You could also compute this directly (but it is better if you have a feel for what the parallax means!) by
d = (7.62"/206265 "/rad)
(2.65 pc x 206265 AU/pc) = 20.2 AU
as expected. Whenever you encounter an orbital problem, you should immediately see if you can use Kepler's 3rd Law in the total mass/reduced mass frame! If possible scale it to our Sun and the Earth's orbit:
2 a3
--> ( M/Msun ) = ( a / 1 AU )3 /
( P / 1 yr )2
which for our problem gives the total mass
.
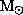Now, we go to the center-of-mass, center-of-momentum frame and use the relation
and thus
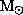--> MA =
2.25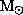
and
.
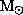We thus have
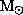L = 23.3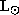 Sirius B: M = 1.05
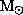L = 0.0296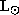
and thus the mass-to-light ratios are
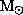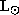
/ Sirius B: M/L = 1.05 / 0.0296 = 35.5
/
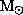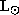
(note that even though the mass of Sirius-B is comparable to the Suns, the luminosity is much smaller - it must be a very different sort of star!).
In class, we discussed the relation between lifetime, the amount of stellar energy available (the mass), and the rate at which energy is expended (the luminosity). Roughly, the lifetime t is given by
and so Sirius B should have a lifetime 35.5 times longer than our Sun's! Likewise, Sirius A is burning up fuel faster, and its lifetime should be only 1/10 of our Sun's.