The goal of this problem is to demonstrate the relation between the intensity and surface flux from a blackbody. Note that in this case, we are computing a radiated intensity and flux, and so the relevant solid angle is *pi*.
In lecture, we discussed the blackbody specific intensity function
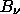(T) =
( 2h
3/c2 )
[ eh/kT - 1 ]-1
which has units of W m^-2 Hz^-1 sr^-1. The Sun has an effective brightness temperature of T = 5770 K. What is the wavelength (in Angstroms Å) at which the blackbody emission peaks? (Hint: use Wien's Law.)
What is the frequency (in Hz) corresponding to the blackbody maximum? At this peak wavelength (frequency), what is the value of the specific intensity B_nu of the blackbody emission? (Be sure to use the flux per unit frequency B_nu, and not the flux per unit wavelength B_lambda.)
After converting this into a emitted surface flux density
= 
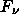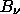
estimate the total surface flux (in W/m^2) by multiplying by the frequency
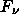
( nu*F_nu is the approximate flux per log-frequency interval or in the band from nu +/- nu/2, where nu is the frequency of the blackbody maximum).
The surface flux from a blackbody like the Sun should be given exactly by the Stefan-Boltzmann equation
T4
where = 5.67 x 10^-8 W/m^2/K^4 is the
Stefan-Boltzmann constant. Compare this exact result to the estimate we
got above pi*nu*B_nu. We often plot nu F_nu when we want to graph flux
density from an intensity.
Sometimes, instead of computing radiated intensities (where the solid angle is effectively pi steradians), we need to compute the received flux, where the solid angle is determined by the apparent angular size of the source of emission.
Because the flux densities encountered in astronomy are so small, in radio astronomy we define the standard unit of flux density (monochromatic flux or specific flux) to be the Jansky (Jy), where
(Note that when we use our blackbody formulae, the results is naturally in MKS units of W m^-2 Hz^-1 sr^-1. You will need to multiply this by the solid angle (to get rid of the sr) and then the conversion factor of 10^26 to get Jy.)
If we observe an astronomical object, like a distant star, we need to calibrate our measurement. The temperatures of the solar system planets depend upon their distance from the Sun (as we found in ASTR011), with Jupiter having a temperature of approximately 122 K (see Appendix A3 of the text). At its closest approach to Earth, Jupiter is 4.2 AU away; Jupiter has a radius of 71400 km. What is the apparent angular radius (in arcseconds) and apparent solid angle (in sr) of the disk of Jupiter at this distance as seen from the Earth? (Hint: make sure to convert between radians and arcseconds correctly, where
and use the small angle approximation
for physical diameter D vs. angular diameter theta radians and distance d.)
Suppose you are observing at a wavelength of 1 cm (frequency 30 GHz). For Jupiter at T=122 K, calculate the value of the blackbody Boltzmann factor
/kT.
You should find that this is much less than 1 (in fact less than 0.1), and thus you can use the Rayleigh-Jeans approximation to the blackbody intensity:
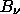(T)
2 k T ( /c )2
=
2 k T / 
2
for h/kT << 1 ,
= c / .
Use this to calculate the blackbody intensity B_nu of Jupiter at 30 GHz, in units of Jy/sr (note the solid angle dependence).
Use the solid angle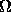 
of the disk of Jupiter at
closest approach found in the previous problem to calculate the observed flux
density (in Jy)
= 
=
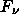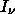
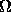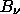
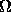
and then by the frequency nu to get our estimate of the received flux
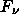
as we did for the emitted surface flux in problem 1. The power (in Watts) received by our telescope is given by multiplying the flux by the physical area A of the telescope
which we will assume has a cross-section given by a circular disk of diameter 10 meters (radius 5 meters) - this is actually a rather small radio telescope. The largest, Arecibo, is over 300 meters in diameter! Compare the power P_rec collected from Jupiter to power levels we are used to, like 1 Watt or even 1 mW (0.001W) like in most computer circuits. This is why radio astronomy is so difficult - the power levels are tiny!
Note that now that we have a calibration, we can now compare a measurement of a radio source to the brightness of Jupiter to get its actual flux density!
The star Sirius (Alpha Canis Majoris) is the brightest star (other than the Sun) in the sky. It has an observed parallax of p = 0.377". What is its distance from the Sun in parsecs?
Sirius is actually is a binary star, with a faint companion. The apparent bolometric magnitude of the bright primary Sirius-A is m_bol,A = -1.55. What is its absolute bolometric magnitude M_bol? Assuming the Sun has an absolute bolometric magnitude of +4.75, calcuate the luminosity of Sirius (in solar units Lsun).
The secondary Sirius-B has an apparent bolometric magnitude m_bol,B = +5.69. Calculate the absolute bolometric magnitude and luminosity of Sirius-B.
The orbit of the Sirius system is nearly edge-on to our line of sight, and has an observed orbital period of 49.94 years. The relative orbit of the two stars is seen to have an apparent semimajor axis a of 7.62". Compute the orbital semimajor axis a in AU, and thus use Kepler's 3rd Law
2 a3
or
to find the total mass M of the system (in Msun).
After careful astrometric monitoring of the system, the individual orbits of A and B about the barycenter of the system are measured, with a ratio of semimajor axes of a_A/a_B = 0.466. What is the ratio of the masses M_A/M_B? Use the total mass found above to find the individual component masses M_A and M_B (in solar masses Msun).
By definition, our Sun has a mass 1 Msun and luminosity 1 Lsun, and thus the mass-to-light ratio for our Sun is M/L = 1 Msun/Lsun. Use the above calculations to determine M/L for Sirius-A and Sirius-B. If all stars burned fuel at the same rate, you might expect that the M/L were the same for all stars. Speculate on what you just found means, both in terms of using the luminosity L to infer the mass M, and the lifetime of the star, if it burns fuel at the rate given by L and has a fuel resevoir proportional to M. (Hint: I am asking you to think through some of the implications. I will do this on most problem sets. I am not looking for a "right answer", but you should write down a paragraph or so trying to use the calculation you just did and see what it might mean in the bigger picture.)
Even this cursory examination of the brightest star in the sky, Sirius, shows us something very strange: the companion Sirius B is similar in mass to the Sun yet is very much less luminous. There clearly are very different classes of stars out there in our very own galactic backyard!
