Quasars --- | ---
Final Exam!
Quasars --- | ---
Final Exam!
Reading:
Chapter 26 (ZG4)
Notes:
pages 109-116
 |
Key Question: | What evidence is there to support or refute the Hot Big Bang model? |
|---|---|---|
 |
Key Principle: | Big-Bang Nucleosynthesis |
 |
Key Problem: | Find out where the microwave background and helium came from. |
There must have been a time in the past when the Universe was hot enough (like the core of a star) for nuclear fusion to occur. Astrophysicists George Gamow and Ralph Alpher in 1948 showed that when T was around a million degrees, protons and neutrons could fuse to form helium. However, nuclear fusion in the early Universe is like an inside out star - the Univserse stars hot and ends cooler. Fusion in a star stars cool as they contract onto the main sequence, then gets progressively hotter as heavier and heavier nuclei are "burned". Because there are initially no heavy elements in the hotter earlier phases of the universe, fusion can only occur near the end when the temperatures are low enough to combine protons and neutrons to make deuterium, a nucleus of "heavy hydrogen":
You should recognize this as being similar to the first step in the proton-proton chain (though there are still free neutrons around then, unlike in stars, so we need not wait until the weak reaction turning protons into neutrons which takes billions of years happens). Thus, only fusion to light elements can occur in the short time that the Universe is cool enough so that the deuterium formed is not broken apart by the high energy photons in the radiation bath of the universe, yet not so cool that the proton-proton chain will not work.
The cosmic nucleosynthesis is a competition between the fusing together and breaking apart by high-energy photons:
At high temperatures, the destruction wins out. Thus, the building of the elements heavier than hydrogen, known as nucleosynthesis, takes place in the temperature range from about 10^8 down to a few times 10^6 K.
Because nuclei in this chain are built by progressive addition of neutrons and protons, it is much like a ladder:
This ladder is built by alternating the addition of protons (which change the nuclear charge by +1 and thus the element) and neutrons (which only change the atomic number or mass and thus the isotope of the given element). However, you will notice that the nuclides with atomic numbers 5 and 8 are marked by "?" - they should be isotopes of lithium (Li) and beryllium (Be) respectively but they are unstable and decay back into what they were made from. Thus to bridge these "gaps" to the heavier elements, you need to add deuterons (the deuterium nuclei pn), not just single protons or neutrons. This is harder to do, and thus there is much less lithium than hydrogen, deuterium and helium-3 and helium-4, and there is essentially no nuclides heavier than lithium-7. All nuclei heavier than these therefore must be formed in the centers of stars. That is why we said earlier that we and the Earth are made from the stuff processed in the centers of stars and blown out by supernove - "star stuff" indeed!
The relative abundances of the nuclides of hydrogen, deuterium, helium-3 and helium-4, and lithium-6 and lithium-7 are controlled by the relative ratios of protons, neutrons and photons at the time of nucleosynthesis. The ratio of baryons (protons and neutrons) to photons at this time means a higher fraction of helium (and deuterium and lithium) in the Universe today. More neutrons relative to protons changes the relative abundances of helium-3 versus helium-4, and deuterium and lithium-7. Using the observed abundances today (though finding a cloud of gas that hasn't been contaminated by supernovae ejecta is difficult) can pinpoint the time of nucleosynthesis. For example, the fact that the mass fraction of helium-4 is around 24% is an important clue.
Gamow and Alpher used the best data at that time and deduced the redshift and temperature of nucleosynthesis. They showed that a consistent picture for early universe nucleosynthesis could be constructed, and furthermore that the heavy elements must have been processed in stars. Finally, they calculated that the current temperature T0 of radiation in the Universe should be about 5 K.
Nucleosynthesis occured approximately 3 minutes after the "Big Bang", or projected point of infinite density and temperature. In the final lecture, we will discuss what likely occured during the first three minutes of the Universe. The Nobel-winning physicist Steven Weinberg wrote a wonderful book called "The First Three Minutes" which I strongly recommend.
The 5 K "cosmic background" predicted by Gamow and Alpher should be seen as microwaves, since from the blackbody formula for the wavelength of maximum emission:
max
= 3 mm / ( T / 1K )
In the early 1960s, a team of Princeton astrophysicists prepared to look for this microwave background using the latest in radio technology. However, they were beaten to the punch by two physicists at Bell Labs looking for a source of excess noise found in transatlantic radio communications. Penzias and Wilson found that no matter which direction they pointed their antenna, they found around 3 K of "excess thermal noise" in their system (even when they cleaned all the bird droppings from their antenna). Discussions with the Princeton scientists alerted them to the correct explanation, that they had found the cosmic microwave background of Gamow and Alpher, purely by accident! Penzias and Wilson would receive the 1978 Nobel Prize for their serendipitous discovery.
As measured by Penzias and Wilson, the microwave background temperature T0 is nearly 3 K, and was seen to be isotropic to better than 10% over the sky. Later measurements improved on this: the COBE satellite launched in 1989 has measured T0 = 2.726 K, and found intrinsic anisotropy only at one part in 10^5! The spectrum of the microwave background is a perfect blackbody to the precision of the measurement. The discovery of the microwave background in 1965 was a vindication of the Big Bang model in that there almost certainly had to be a time when the Universe was hot, dense, and opaque to photons at the redshift z ~ 1000. The competing model at that time, the so-called steady-state universe where the expansion was compensated for by the continuous creation of matter so the same density could be maintained indefinitely (and an infinitely old universe), was thus discredited, though some stubborn adherents still try and tweak it so that it seems to work (though it smells of epicycles).
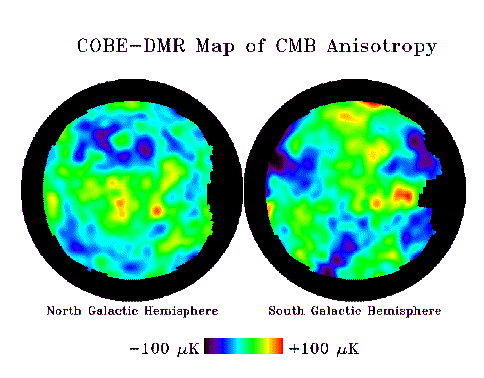
One of the prime missions of the COBE satellite was to measure the anisotropy of the cosmic microwave background radiation - in other words, whether the temperature (brightness) of the radiation in different directions on the sky is different from the 2.726 K average. Changes in brightness of the radiation reflect changes in the density of the Universe at the time of recombination at z = 1000. At this point the Universe was only about a million years old, and there were only very small variations in the matter and radiation density that would grow gravitationally over the course of 15 billion years to form all the galaxies and varied structures we see today! Here are some maps of the sky (at a wavelength of about 3mm) made by the COBE satellite in its 4-year lifetime:
The upper panel shows a strong variation in the temperature (coded from blue to red, with blue cooler than the average and red hotter than the average) from one side of the sky to the other. This pattern is called a dipole and is simply due to the Doppler effect from our galaxy's (and thus the Earth's) velocity of around 570 km/s (caused by the gravitational pull of the Virgo cluster and the so-called "Great Attractor"). The magnitude of this dipole is 10^-3 of the T0. Q: How does this relate to v/c of the Earth's velocity?
The middle panel shows the variations after subtracting the dipole. The bright band across the center is radio emission from our galaxy. Note that the map is in galactic coordinates with the galactic center in the middle!
The bottom panel shows the microwave background with the dipole and the galaxy subtracted. Alot of the hot and cold spots are just instrumental noise, but some of these (the signal-to-noise ratio is about 2) are real fluctuation in the 2.7K background caused by very small density fluctuations at z=1000 when the radiation was last scattered by the ionized Universe! The level of the fluctuations are around 10^-5 of the 2.726 K average background, very tiny indeed. Here is a better map of the cosmic microwave anisotropies from the COBE map:
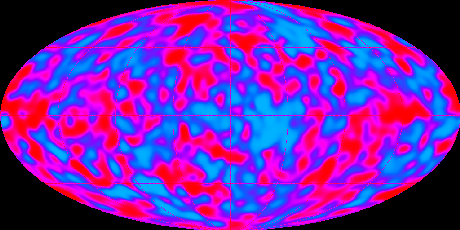
The resolution of COBE was only around 7 degrees. This map has been smoothed to 10 degrees. For more on the results from COBE see the COBE Home Page at NASA.
On smaller angular scales, maps of the microwave background can be made from ground-based telescopes. My PhD thesis at Caltech was on observations looking for anisotropy on angular scales of 2' to 7' (arcmintues). For a brief description of this work, and my current microwave background work, see this page.
Some microwave background experiments:
| Time since 0 | Event | Description | Temperature |
|---|---|---|---|
| 15 x 109 yrs | Now | Galaxies, stars, planets, and us | 3 K |
| 109 yrs ? | Galaxy formation | bulges and halos of normal galaxies form | 20 K |
| 106 yrs | Microwave Background | recombination - transparent to photons | 3000 K |
| 3 min | Nucleosynthesis | light elements formed | 109 K |
| 6 sec | Electron-Positron pairs | creation of electrons | 6 x 109 K |
| 2 sec | Neutrinos decouple | creation of neutrino background | 1010 K |
| 2 x 10-6 sec | Proton-Antiproton pairs | creation of nucleons | 1013 K |
| 2 x 10-10 sec | Electroweak unification | E-M and weak force same | 1015 K |
| 10-35 sec ? | Inflation | universe exponentially expands by 1026 | 1027 K |
| 10-35 sec | Grand Unification | E-M/Weak and Strong forces same | 1027 K |
| 10-44 sec | Quantum Gravity | Unification of all 4 forces | 1032 K |
| < 10-44 sec | Planck Era | No concept of space or time? | > 1032 K |
We used Einstein's equation from special relativity E=mc^2 to calculate the energy converted from mass in nuclear reactions. It is allowed to convert energy into mass also! Two photons of sufficient energy E can interact to create a particle and antiparticle of mass m=E/c^2 or less. Since photons have no charge and are not normal particles, conservation of quantum numbers (like charge, baryon number, and others more obscure) require that particles be created in pairs, along with an antiparticle (which has all quantum numbers reversed compared with the particle). You need two photons for momentum conservation.
The rest mass of the electron is m_e = 9.11 x 10^-30 kg, and thus two a photons of energy E = m_e c^2 = 8.20 x 10^-13 J (511 keV) each or greater can create an electron-postitron pair! Likewise, the proton mass is m_p = 1.67 x 10^-27 kg, so two photons of energy 1.5 x 10^-10 J (938 MeV) each or more can created pairs of protons and antiprotons. Note that the particle and antiparticle will usually come back together in a short time, or encounter another of its anti-partners, and annhilate turning into energy (photons). (Note: particle - antiparticle annhiliation is a possible source of energy, assuming you can find antiparticles sitting around somewhere, and is perfectly efficient in the sense of E=mc^2. This should be familiar from "Star Trek" as their stated source of energy for the starship.)
The average energy of photons in a thermal radiation bath is about E=kT, where k is Boltzmann's constant (k = 1.38 x 10^-23 J/K). Thus, when the temperature reaches T=mc^2/k then particle-antiparticles pair with masses m can be created (and destroyed) at will. For electrons, this will occur at temperatures of just under 10^10 K, which occur in the universe at a few seconds after the big bang. At times earlier than 1 second, therefore, the Universe was a sea of electrons and positrons being created and annhiliation spontaneously. Likewise, when the Universe was just above 10^13 K, protons and antiprotons could be created from the radiation, and thus earlier than 10^-4 seconds after the big bang the Universe also had a sea of protons and antiprotons being continuously created and destroyed.
There are four known forces in nature: strong nuclear, electromagnetic, weak nuclear, and gravity (in decreasing order of strength with ratios of 1:10^-12:10^-14:10^-40 with ranges of 10^15m, infinity, 10^-17m, infinity respectively). In the late 19th century, James Clerk Maxwell unified the electric and magnetic foreces as aspects of the same phenomenon, electromagnetism. His four equations describe the electric and magnetic forces experienced by charged bodies. Can this be done with all the forces? It is certainly philosophically appealing to think that all the forces of nature are aspects of a single underlying theory!
In our current paradigm for physics, the standard model, as well as most viable alternatives, the forces become unified as the energy of particles undergoing the interactions increases. At high energies, you cannot tell the difference between any of the forces, and it is only at low energies where we experience the universe that the four fundamental forces become distinct. This idea is related to the concept of symmetry in modern physics, since a perfectly "symmetric" universe is one where everying is interchangeable, particles and forces for example. Thus, the forces and particles become differentiated through the mechanism of spontaneous symmetry breaking, which gives particles their different masses (why is the proton more massive than the electron?) and forces their different strengths and couplings to particles (why is the strong force stronger than the weak force?).
The weak force is intermediated by the W and Z particles. The W and Z have measured masses of around 90 GeV (1 GeV = 10^9 electron volts energy equivalent mc^2. Thus, the proton mass is 0.94 GeV.) The neutral Z is slightly heavier than the charged W+ and W-. Thus, at T of about 10^15 K, W and Z bosons can be created and destroyed out of photons, and thus we might expect the electromagnetic force carried by photons and the weak force carried by the W and Z to be indistinguishable. Indeed, at this temperature and higher the electromagnetic and weak forces are unified into the electroweak force. The electroweak theory and unification was verified about 15 years ago in particle accelerator experiments. The electroweak unification occured approximately 10^-12 seconds after the big bang in our model.
Given the success of the electroweak unification theory, we might confidently expect to be able to unify the electroweak and strong nuclear forces at even higher energies. In fact, Einstein himself spend his last years looking for such a grand unified theory or GUT. From the strength and nature of the strong force, we expect that this should occur at energies of 10^14 GeV (10^23 eV) corresponding to temperatures of 10^27 K. Unfortunately, this energy is well above the capabilities of current and projected future accelerators (around 10^12 eV), but there some lower energy aspects of GUTs that can be tested even at these energies. We expect that at temperatures above 10^27 K and higher, which occurs 10^35 seconds and earlier after the big bang, the electro-weak-strong forces are unified, and only gravity stands alone. Also, at this so-called GUT transition when the strong force split off, some theories state that there was a phase in the evolution of the Universe where a cosmological constant dominated - this is the era of inflation described below.
We now revisit Einstein's cosmological constant by amending the energy equation. Consider first the standard energy equation with kinetic and potential terms:
It is easiest to rearrange this to solve for the velocity:
What about the energy term E/m? It seems sensible that it be related to the relativistic energy E=mc^2. If we write E = -k mc^2, where k is some constant, then E/m = -kc^2. Then
For a flat Universe, k=0. It turns out that k=+1 for a closed universe and k=-1 for an open universe. Other values of k are not allowed by the equations of general relativity. Note that we can see if k=+1, then you cannot have R > 2GM/c^2 or you will get negative v^2 - this is the closed universe.
Now, we can add the cosmological constant term, not as a constant (kc^2 is already a constant in this equation) but with an R^2 dependence so it will behave as a density:
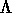R2
The consta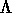nt (Lambda) is the cosmological
constant.
Note that the effect of Lambda grows with R, and thus the expansion rate of the Universe increases with time. Note that the cosmological constant term dominates the evolution of the right-hand side of the equation when
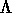> 2GM/R3
or
>
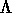8
G
/3.
In that case, the universe will expand with v proportional to R, and thus (using calculus) you find that
This is exponential expansion. We will use this in the very early universe to drive inflation.
Let us explore the possibilities in this modified energy equation. Note that Einstein used it to make a static universe by noting that if we ignore the curvature term kc^2 and if Lambda = -(8Pi G rho/3), then v=0 is the solution, and a static universe (with constant density) is possible. This is what he later called his greatest blunder since v was found to not be zero. Note also that if Lambda is even slightly different than -(8Pi G rho/3), then we get a nonzero v.
The implications of having a cosmological constant that is now greater than the density term means that the Unverse is older than if the Universe had Lambda=0. This is because the Universe was expanding slower in the past when Lambda was on the order of (8Pi G Rho/3). Thus, if Lambda is large enough, then the age problem can be remedied. This one of the proposed solutions to the age problem, and allows a flat universe (k=0 determines the topology, not Lambda) with a moderate H_0=82 km/s/Mpc, but does require a rather high value of Lambda. There are some measurements being done now that could rule this high a value of Lambda out (these are based on the counts of things like gravitational lenses with redshift, looking for a pile-up when the universe was just changing from density to cosmological constant dominated evolution.
As we stated when we began our investigation into cosmology, by and large we seem to live in a Universe that is homogeneous and isotropic. In particular, we look in two very different directions on the sky, we find that the structure of the Universe appears the same. For example, except for the dipole due to our own velocity through space, the cosmic microwave background radiation appears to be isotropic to the level of 1 part in 10^5 or so, even on opposite sides of the sky. The crucial question is: How did the Universe know to make the cosmic background 2.726 K in every direction that we see? This may seem like an unimportant question, or some sort of metaphysics, except for the fact that in our model for the expanding universe, those parts of the universe could never have communicated with each other at the speed of light! Recombination occured about a million years after the big bang, which was some 15 billion years ago - that's how long it took light to reach us from when the microwave background was last scattered and its temperature and fluctuation level imprinted. Thus, it would have taken twice that, or a couple of million years less than twice the present age of the Universe for any information, forces, photons or particles to have interacted between these regions. One of the cornerstones of physics is the concept of causality, that for something to "cause" something else to happen, some interaction must have taken place which occurs at the speed of light at a maximum. Thus, two regions of space have been separated by a distance equal to or less than the light travel time between for the age of the Universe are said to have been in causal contact. Patches of the sky separated by an angular distance of more than 2 degrees were never in causal contact at the time that the microwave background was generated. In general, it is difficult to see how the Universe seems homogeneous and isotropic on scales that were never in causal contact given our expanding universe model.
Of course, it could be solved by resorting to special initial conditions. The subsequent evolution of a system (like the Universe) under physical law is given by the inital conditions to say what we started with and the laws of physics to tell us what happend to them - you should end up with the Universe as we observe it now if you have the right model. Thus, we could put the isotropy of the Universe as we see it down to the assumption that it started out very homogeneous to begin with. However, it is much more satisfying if we have some physical reason that the Universe should appear isotropic, like it were mixed by heat and convection like the atmosphere of a star. But this requires causal contact. The maximum distance which two points in causal contact can be is called the horizon. This is a different sort of horizon from, but related to, the event horizon we encountered when discussing black holes. The problem of causality between two distant part of the observable universe is called the horizon problem.
The solution is to modify the evolution of the Universe to make regions now far apart even closer than they would be under the normal expanding model at very early times. Thus, we need to change the energy equation to allow faster than normal expansion early on. When we discussed the effect of a positive cosmological constant in Einstein's equation, we noted that if the cosmological constant term were large enough, you would get exponential expansion, or inflation of the Universe:
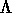R2
becomes, as before, when the W term dominates
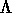R2
Using v=HR, we find that H is constant H^2 = W, and thus (using calculus) that if R=R0 at t=t0 at some point during inflation, then
For the universe to be as isotropic as we see it and yet purely causal, it turns out that the universe must have inflated by a factor of e^60 or more (10^26 or more).
If you think a bit, however, you should notice a problem in a cosmological constant to drive inflation: how do you stop it? The exponential inflation with H^2=W will go on forever unless we get rid of the W term after the universe has inflated sufficiently. If for some reason W were to drop to zero (or at least much smaller than 2GM/R^3), then the normal Hubble expansion as determined by the density would take over. It turns out that using our standard model for particle physics, there are indeed mechanisms for causing inflation, expanding the Universe by 10^50 or so, then safely turning off inflation. There are some theoretical indications in our theory that this occured at the time of the GUT transition at 10^27 K. The mechanism of inflation is widely, though not universally, accepted among cosmologists as having occured in the very early Universe.
One of the consequences of inflation is that after expanding by such a large amount, the curvature of the Universe at the end of inflation should be very nearly flat. Most cosmologists who calculate inflationary models would say that inflation predicts a Universe that is flat, and thus very nearly the critical density. This solves another problem in cosmology, called the flatness problem. It appears observationally that the universe is at least within a factor of 10 of the critical density, that is that the observed density is 10% or more of the critical density. In the expansion (after inflation) the Universe diverges from the critical density, thus if it is within a factor of 10 now, it had to be nearly the critical density much earlier on. This is another worrisome case that would require fine-tuning of the initial conditions (causality and all that). Inflation leads naturally to a very nearly flat universe. The only problem is that most models of inflation naturally lead to a Universe much closer to the critical density than a factor of 10. Thus, inflation may do too good a job of solving the flatness problem if observations indicating that the current density is only 10%-40% of the critical density. The jury is still out on what our density really is, but this may be a potential problem with the inflationary theory.
Also, more work needs to be done on the details of the exact physical mechanism involved in the inflation (what particles are involved, how long it went on, whether gravity waves were generated). It is interesting that in order to get rid of the cosmological constant W at the end of inflation, it energy which was driving the expansion of space must be turned into something. It turns out it is converted into radiation and particles (thus making the matter-energy density the critical density), and that all the matter and radiation in the universe today was generated from the cosmological constant energy at the end of inflation. All the matter and energy density that was present before inflation was "inflated away" to low densities by the exponential expansion. Kind of cool, eh?
Paul Steinhardt, professor of Physics and Astronomy at Penn, has been a pioneer in the development of the inflationary theory in cosmology. See also the Cosmology and Astrophysics at Penn page for a description of this and other cosmological research at the University of Pennsylvania.
To unify the final (?) force, we need to go back even farther to temperatures of 10^32 K at a time 10^-43 seconds after the "big bang"! The energy of this full unification can be estimated by considering what it might mean for photons and gravity to be equivalent. For example, is there an energy where a photon can create a relativistic massive particle that is its own black hole? If we remember what we've done before, we can see that this will occur when the wavelength (h/mc) is equal to the Schwarzschild radius (2Gm/c^2):
G
(where I have put in the correct factor of Pi to make it come out right). This mass is called the Planck mass, and is equal to 10^19 GeV (or 10^32 K). Q: Calculate the Planck mass in kilograms, and the equivalent energy in Joules and electron volts, and temperature in Kelvin..
At these energies and higher, there will be the creation and destruction of these black hole -like particles. Since we learned from general relativity that gravity means the curvature of space-time, then at these energies and higher, the concept of space and time breaks down! (Is this another sort of unification and symmetry?) In fact, the theory that must describe this will have to put gravity on the quantum mechancial level (since the wavelength of the black hole is equal to its size) - this is called quantum gravity, and this earliest (?) phase of the Universe is known as the Planck Era. Since we have no workable theory of quantum gravity (though there are some intriguing possibilities), we really do not understand the Universe at times earlier than this (of course, it is likely that time as we know it is not relevant in the Planck era). This can in some sense be considered to be the "Big Bang", where in our space-time continuum came into being.
The NCSA has put together a fascinating exposition Cosmos in a Computer featuring some of the latest state-of-the-art simulations of our Universe. Be sure to try the exhibit map to navigate the site.
The picture I have given you of the Universe should be taken seriously not because it is written in a textbook, but because we can calculate the relevant quantities using the laws of physics, which were in turn built upon a sequence of observations, hypotheses, theories, then further observations.
I hope you enjoyed this class, and feel that you learned something about this Universe we inhabit. I have pushed you pretty hard to be able to calculate some pretty important things about the Universe, and you should feel pretty good about your performance - you have been astrophysicists for this semester!
Prev Lecture ---
Astr12 Index ---
Astr12 Home
smyers@nrao.edu Steven T. Myers