Lecture 25 - Cosmology (4/20/99)

Prev Quasars --- | --- Early Universe Next

ASTR012 Reading:
Chapter 25 (ZG4)

Notes:
pages 102-108


The Coma cluster of galaxies. (Courtesy Omar Lopez-Cruz and Ian Shelton/ U.Toronto)
? Key Question:   What is the fate of the Universe?
! Key Principle:   The cosmological energy equation
# Key Problem:   Calculate the critical density of the Universe

Investigations:

  1. The Great Attractor
  2. Newtonian Cosmology
  3. Evolution of A "Critical" Universe
  4. More on FRW Cosmologies
  5. General Relativity and Cosmology

Large Scale Simulations of the Universe

Astrophysicists are also engaging in large numerical simulations of how we think the universe would evolve under different assumptions about the matter therein. Some of the faculty in this department are involved in these endeavours. Check out some of the links to our work, and other related projects.


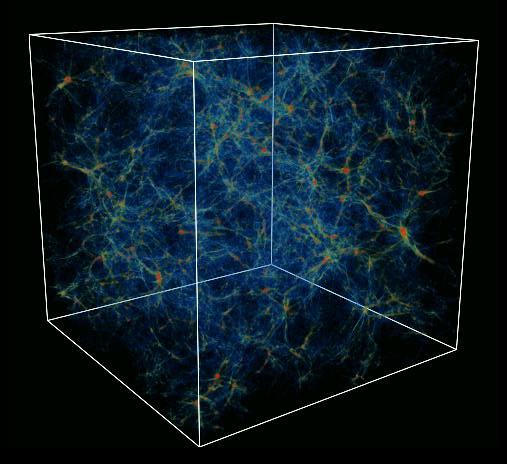
A simulation of a box 85 h-1 Mpc on a side, using a model with a cold+hot dark matter. Courtesy Greg Bryan and Mike Norman (U.Illinois/NCSA/GC3)

The Cosmic Energy Equation

Because the laws of physics are mathematical, two systems that follow similar laws will behave similarly. We used this when we computed the orbits of electrons about the nucles, noting that the electric force law was similar to the gravitational force law. If you remember when we calculated the energy levels of the atom and when we calculated the escape velocity from a gravitating body, we used an energy equation. Can we make an energy equation for the Universe?

Consider a sphere of radius R comoving (that is, expanding along with the Universe) enclosing a mass M. The gravitational energy equation would give:

E/m = v2/2 - GM/R

Note we have divided through by the test mass m, the mass of the particle that is feeling the force from the total mass M at the edge of the sphere at radius R. If you remember the gravitational case, if E=0, then at R of infinity v=0 and the system was just unbound. If E<0, then the system was bound and the velocity v would reach zero at a maximum radius

Rmax = -GM(m/E)

and the particle would then fall back. If, on the other hand, E>0, then v would be positive even for R of infinity, and the system is unbound. If we had a fixed measure of the velocity, then we could think of an escape mass Mesc, for which with E=0, v would be zero at R of infinity:

Mesc = v2 R / 2 G

If we want to apply this to the Universe, we should use the mass density in the sphere (3M/4Pi R^3) instead of the mass

3Mesc/4Pi R3 = 3 v2 / 8 Pi G R2

In an expanding universe, v = H R on the comoving sphere, and so

3Mesc/4Pi R3 = 3 H2 / 8 Pi G

which no longer depends on R! This density, 3H^2 /8Pi G, is called the critical density of the Universe. If the average mass density in the Universe is equal to or less than this, then the Universe behaves as if it is unbound and it will expand forever. If the average mass density of the Universe is greater than the critical density, then it will expand to a maximum scale length, then recollapse, behaving like it is a bound system.

The case with a density greater than critical gives as a closed universe with positive curvature, finite volume, which will expand for some time, then begin to recollapse. The case with a sub-critical density corresponds to an open universe with negative curvature which will expand forever, and is infinite in volume. A universe with the critical density is flat, infinite, and will expand forever though slowing down toward zero at infinite time in the future.

The question of whether we live in an open, flat, or closed universe is a matter of what the mass density of the Universe is relative to the critical density 3H^2 /8Pi G. For a Hubble constant of H = 82 km/s per Mpc as measured by HST, the critical density is 1.26 x 10^-26 kg/m^3. This seems really tiny, but space is really big. (Q: What is this critical density in units of solar masses per cubic Megaparsec?) In fact, it appears that our Universe may have only about 30% of the critical density, and we might be living in an open universe. On the other hand, this is a hard measurement to make, and there are some indications (as well as some theoretical prejudices) that we live in a flat (or very nearly flat) Universe.

Cosmological Scale Factors

In an expanding universe, the scale factor changes with time, and thus with apparent distance. The radius R of an imaginary sphere, of radius R_0 (say 1 Mpc) now, will change as the universe expands. Similarly, the wavelength of light moving through the Universe will also expand (red-shift). The ratio R/R_0 is thus related to the redshift:

R(z) = R0 / ( 1 + z )

Note that R_0 = R(z)( 1 + z ) is the redshift relation for light of true wavelength R(z) emitted at redshift z and observed here as an increased wavelength R_0.

For small redshifts, the Doppler shift is approximately z = v/c, while the Hubble velocity is approximately v = H d. Thus, the distance - redshift relation is approximatley

d = c z / H

This is true for any curvature Universe on small enough scales, since it just involves the local expansion rate.

Introduction to General Relativistic Cosmology

What can we "see" about the Universe? It is certainly apparently very large, as the most distant quasars (at z = 5) are over 4000 Mpc away. It appears to be in the process of uniform expansion, with the Hubble relation v = H d. Finally, on the largest scales it appears to be approximately homogeneous and isotropic as per the cosmological principle. It turns out from these considerations alone, and using Einstein's General Theory of Relativity, one is led to some concrete predictions for the evolution and topology of the Universe as a whole. This is subject of cosmology, the study of the Universe as an entity.

Soon after the publication of his General Theory of Relativity in 1916, Einstein applied his equations of gravity to the Universe as a whole. However, when he did so he ran into a problem: the equations predicted a Universe that was in the state of expansion or contraction, but not stasis. Remember, this was in 1917, before the discovery of the expansion of the universe by Hubble in 1929, and the philosophical prejudice was that the Universe was unchanging, static, and perhaps everlasting. (Q: Compare this prejudice to those of pre-Copernican cosmology and of pre-Darwinian biohistory.) Einstein found he had to add a new term to his equations, the so-called cosmological constant, to end up with a static universe neither expanded nor contracted.

When Hubble discovered the expansion of the Universe in 1929, Einstein found that his equations without the cosmological constant made sense. He then declared that the cosmological constant was his "greatest blunder". He felt that he should have had faith in the predictions of his theory, and disregarded the unfounded (that is, not based upon observation) prejudice for a static universe. However, in the last decade, a number of observations of the Universe have been found to be at odds with some theoretical predictions using simple cosmologies. Some solutions to these problems involve the introduction of a cosmological constant term into Einstein's equations, though in a somewhat different manner than for a purely static universe. Thus, this may not have been a blunder after all!

Spacetime Curvature

Just like spacetime is curved by the presence of mass like a black hole, the spacetime of the Universe as a whole is curved by the presence of mass (like ourselves). There are three generic topologies for a homogeneous and isotropic Universe with 3 spatial dimensions like ours. They are distinguished by the curvature. In one dimension, like a line, there is only one sense of curvature. However, in two or three dimensions, curvature has a sign, and is positive, negative or zero. For a homogeneous and isotropic, both the sense and magnitude of the curvature must be uniform, that is the same everywhere.

It is easiest to use a two-dimensional analogue to begin with. A sphere has positive curvature. In two orthogonal (perpendicular) directions, the curvature is in the same direction, so a positively curved space closes back on itself, like a sphere. A positively curved space is unbounded, but finite (like the area of a sphere). A plane has zero curvature, and is thus flat. Flat space is unbounded and infinite. A saddle has negative curvature. Orthogonal directions show curvature in opposite directions (upward or downward). A space with negative curvature is unbounded and infinite.

Note that geometery as we are first taught it is only good in flat space. This is Euclid's geometry, and thus flat (zero curvature) space is also called Euclidean. (Note: flat space is Euclidean, but flat spacetime is Lorentzian, because time behaves differently than space. See the Special Lecture on the speed of light for more details.

There are several things that are different in non-Euclidean spaces, and can be used to tell if you are in curved or flat space. For example, one of Euclid's postulates is that parallel lines never meet (if they are not identical). Note that in positively curved space this is not true! Two parallel lines on a sphere are great circles, and two distinct great circles meet on opposite sides of the sphere at two points. The circumference and area of a circle, and the sum of the vertex angles of a triangle are also different in differently curved spaces.

In positively curved space, the circumference of a circle is less than Pi x Diameter, and the area less than Pi x Radius^2. In 3-D, the volume of a sphere is thus less than 4/3 x Pi x Radius^3! Furthermore, the sum of the three vertex angles of a triange are greater than 180 degrees! (Q: Test these statements using a globe (sphere). For example, cut a circle and triangle out of paper. Now try and paste it onto the sphere. What do you have to do to these figures to make them conform to the sphere?)

In negatively curved space, the circumference of a circle is greater than Pi x Diameter, the area greater than Pi x Radius^2, and the volume of a sphere thus greater than 4/3 x Pi x Radius^3. The sum of the vertex angles of a triangle are less than 180 degrees. (Q: Try and demonstate these properties of negatively curved space. Though you cannot easily make a 2-dimesional negatively curved uniform surface, you can use a saddle-shaped surface that has negative curvature at its "saddle point". Try pasting a circle and triangle there.)

Of course, the Universe is very large, and its curvature slight, so you would have to use very large circles or triangles to do these tests!

The Age of the Universe

If we live in a Universe that is expanding with mass in it, the expansion is slowing down. Thus, the Hubble constant H was higher in the past when the Universe was expanding faster. We denote the current value, which we measure around us locally, as H0. H0 as measured by HST is 82 km/s/Mpc, though different measurements give values in the range 40 to 100. A universe with higher density is younger than a universe with lower density, given the same expansion rate H0 now, since it will have slowed down more from a higher expansion rate earlier on.

If there were no mass in the universe, then H0=H always and it would expand at the same rate. The age of such an empty universe would thus be

t0 = 1 / H0

This represents the maximum age of an expanding universe with a given current value of H0 (though we will find we can change this by changing the energy equation). For H0=50 km/s/Mpc, the age of an empty universe would be just under 20 billion years, and thus for H0=82 it would be around 12 billion years old. Since the oldest globular clusters seem to have ages of 15 to 18 billion years, then we might expect that H0 would be near 50. Thus, the HST value of H0=82 is incompatible with old globular clusters even for an empty universe. Perhaps astronomers are mistaken about the globular clusters ages (new calculations are being done for stellar evolution). Another possible solution, using a cosmological constant, will be discussed in the next lecture.

If we live in a flat universe with the critical density, things are even worse. The age of a flat universe is given by

t0 = 2 / 3 H0

so for H0 = 50 km/s/Mpc the age t0 is 13 billion years, and for H0 = 82 is 8 billion years! This is the so-called age problem in cosmology, and we are working very hard to see what the solution is. To summarize, the oldest globular clusters appear to be 15 to 18 billion years old, while the Sun is around 4.5 billion years old. If H0 is really as high as 82 km/s/Mpc, and the Universe were flat, then the Universe would be younger than its oldest stars, which is nonsensical. Either we have gotten the globular cluster ages wrong, or H0 is really 50 km/s/Mpc or smaller, or there is some other term in the energy equation that is making the Universe expand faster now than in the past.

Although the relationship between the redshift and time is complicated, there are two simple cases. For an empty universe with constant expansion rate:

t = t0 / (1 + z)

For a flat universe

t = t0 / (1 + z)3/2

These give the age of the universe t at redshift z.

The Density of the Universe

We have from the previous lecture the scaling of lengths with redshift

R(z) = R0 / ( 1 + z )

The density of matter in a sphere of radius R is given by 3M/4Pi R^3, so

(z) = (now) x ( 1 + z )3

The matter density in the Universe was higher in the past. Note however that the critical density 3H^2/8PiG was also higher in the past, since H was higher (expanding faster). It turns out that for a flat universe at the critical density, the density always remains at the critical density (since it must always be flat). Therefore, it must be that

H^2 = H0^2 ( 1 + z )3

to keep up with the matter density, and thus

H(z) = H0 ( 1 + z )3/2

Radiation (all the light in the Universe) also has a density that will increase in number of photons per unit volume as (1+z)^3 just like the matter density. However, the energy of the radiation is being redshifted away, and must have been higher in the past by the factor

E(z) = E0 ( 1 + z )

where E = h f = h c / Lambda the wavelength. Thus, the energy density of the radiation evolves as

urad(z) = urad(0) * ( 1 + z )4

Since the energy of matter goes as mc^2, the energy density of matter is

umat(z) = umat(0) * ( 1 + z )3

Thus, at some point in the past the two were equal, Umat=Urad. This occurs at 1 + z = u_mat(0)/u_rad(0). Currently, the energy of the Universe is matter dominated with Umat/Urad around 10^4. Thus, at a redshift z of around 10^4, the energy density in matter and in radiation were equal. Before this, at higher redshifts, the Universe was radiation dominated with most of the energy in photons!

The Stefan-Boltzmann law is essentially a statement about the energy density of radiation. We can rephrase it as

urad = a T4

(Note: the Stefan-Boltzmann constant "sigma" is equal to ac/4.) Thus, the temperature of the radiation must also be higher in the past by the factor

T(z) = T0 ( 1 + z )

The Universe was hotter and denser in the past. This statement turns out to have profound consequences, and follows from the expansion of the Universe and the theory of relativity. In fact, if we carry it to its extreme, there must have been a point (as it turns out not infinitely far back in time) when the universe was infinitely dense and infinitely hot - this is the point called the "Big Bang". This fiducial beginning is the point from which the age of the Universe is measured. Q: What does the current temperature of the radiation in the Universe T0 represent? How could we measure it?

Cosmology in Outline

  1. Clustering in the Universe
  2. Introduction to Cosmology
  3. Is the Sky Dark at Night?
  4. The Expansion of the Universe revisited
  5. General Relativistic Cosmologies
  6. Spacetime Curvature
  7. Cosmological Scale Factors
  8. The Energy Equation
  9. The Age of the Universe

Prev Prev Lecture --- Next Next Lecture --- Index Astr12 Index --- Home Astr12 Home

smyers@nrao.edu Steven T. Myers