Lecture 15 - Stellar Energy (3/4/99)
 Star Formation --- | ---
Stellar Evolution
Star Formation --- | ---
Stellar Evolution

 Reading:
Reading:
Chapter 16-1, 16-2 (ZG4)
Notes:
pages 57 - 61
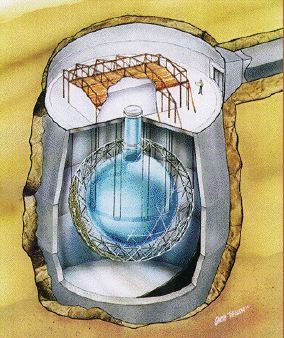
Artists conception of the
Sudbury Neutrino
Observatory. Observation of solar neutrinos can probe conditions
at the very core of the Sun. (Courtesy SNO)
 |
Key Question: |
What energy source powers the Sun?
|
|---|
 |
Key Principle: |
Nuclear Binding Energy
|
|---|
 |
Key Problem: |
Calculate rate of Fusion in Sun.
|
|---|
Investigations:
- Stellar Energy
- What is the energy generation (Watts per kg) required to supply the
luminosity of the Sun?
- What is the gravitational potential energy available in the
Sun?
- How long could this supply the current solar luminosity?
- How much energy per nucleon is needed over the solar lifetime
of 10 billion years?
- What is the binding energy of the electron in hydrogen? Could
this supply the energy?
- Nuclear Binding Energy
- What does the relativistic energy equation E = gamma*mc^2 imply?
- What is the rest mass of the proton (in MeV/c^2)? The
electron?
- What is the approximate Coulomb barrier in a nucleus?
- Are there energy levels in the nucleus as in the electron orbitals?
- Can we extract energy from changes between these levels?
- What is the binding energy curve (E/nucleon vs. #nucleons) for
atomic nuclei?
- When does fusion liberate energy? When does fission?
- How does the change in biniding energy show up in the mass?
- What is the mass defect of a helium-4 nucleus versus four
protons?
- How much energy per nucleon can be extracted by fusion four protons
to make a helium-4 nucleus?
- What fraction of the rest mass of a proton is converted into energy
in this process?
- What fraction of the Sun's hydrogen must be fused into helium over
its lifetime to supply the current luminosity?
- The Proton-Proton Chain
- Approximately what is the thermal energy required to overcome
the Coulomb barrier? What temperature does this correspond to?
- What is the main proton-proton chain (PP I)?
- What step takes the longest to occur? Why? What is the implication
of this?
- What is the significance of neutrinos in the P-P reaction? How many
are generated each second?
- What are the PP II and PP III chains?
- Where do high energy solar neutrinos come from?
- What is the solar neutrino problem?
- How do you detect solar neutrinos?
- Other Fusion Chains
- At what temperature does the P-P reaction "turn on"?
- What is the CNO cycle? Why is it equivalent to P-P?
- At what temperature does CNO turn on? When does it dominate PP?
- What are the temperature dependences of PP and CNO?
- What is the triple-alpha process or helium burning?
- What are the temperature thresholds and reactions in carbon, oxygen,
and silicon burning?
- How do you get heavier nuclei to fuse in a star?
- What happens when you try to fuse iron-peak elements (Fe, Co, Ni)?
Solar Neutrinos:
Neutrino Astrophysics has a long tradition at Penn. There is a good
discussion of the
implications of the results of solar neutrino experiments set up by
the group.
Some links to neutrino experiment sites:
Stellar Energy in Outline:
- Nuclear Energy in Stars
- We showed in previous lectures that chemical energy was insufficient
to power the Sun. Even gravitational energy, which could provide
the Sun's luminosity by shrinking by 40 meters every year, could
only do so for millions of years, not the billions that the Sun
has lasted.
- Since the gravitational and the electromagnetic forces are
insufficient to provide the energy of the Sun, we turn to the
remaining forces:
the strong and weak nuclear forces. In particular, it is the strong
nuclear force that can provide us this energy.
- The strong nuclear force is the force that holds protons and
neutrons together in the nucleus of the atom, overcoming the mutual
electrical repulsion of the protons. The strong force is carried
by particles called gluons, which hold together the
quarks that make up protons and neutrons. (Electrons are
not made up of quarks - they are a different sort of particle
called a lepton.)
- The weak nuclear force is a force that changes the kind of
quark or lepton. The weak force is the kind of force that can
change a proton into a neutron, and visa versa, for example.
- Just like we can emit a photon (energy) by moving an electron
into a more tightly bound orbit, we can liberate nuclear energy
in the form of photons and other particles by making the nucleus
more tightly bound.
- It turns out that for elements ranging in mass from hydrogen
to iron, the nuclei are more tightly bound as you increase the
mass. For elements heavier than iron, the nuclei are less tightly
bound the more massive they are.
- This means the for elements lighter than iron, you can release
energy by the fusion of more than one together to make a heavier
nucleus.
- Similarly, for elements heavier than iron, you can release energy
by causing fission of a heavier nucleus into more than one
lighter fragments.
- The way to measure the energy released in the fusion or fission of
nuclei is to measure the mass of the nuclei before and after the
reaction.
- Einstein's equation relates the mass and the equivalent energy:
E = m c^2
- If you could convert all of a proton's mass (1.673 x 10^-27 kg)
into energy, you would get (1.67 x 10^-27 kg)(3 x 10^8 m/s)^2
= 1.506 x 10^-10 Joules. In more familiar units, this is
equal to 938 x 10^6 eV or 938 MeV(millon-electron-volts).
There is a tremedous
amount of energy available in the mass of particles.
- For comparison, the mass of the electron gives 511 x 10^3 eV
of energy, or 511 keV (kilo-electron-volts).
- Often the masses of particles are given in energy units of mc^2,
so the proton mass is 938 MeV, and the electron mass is 511 keV.
Note that you can also reverse the process, and given 938 MeV of
energy you can create a proton! (It turns out you can't just
create a proton, you have to create an anti-proton also. We
will discuss this later on).
- Thus, if you take four hydrogen nuclei (protons) and convert them
into one helium nucleus (2 proton, 2 neutrons), you find that the
sum of the 4 proton masses is 0.7% larger than the mass
of 1 helium nucleus.
- This difference in mass comes out in energy (photons and particles).
The amount of energy is calculated by E = m c^2, where m is the
mass difference, in this case 4.8 x 10^-29 kg which gives 27 MeV
of energy. Compare this with the 50 eV or so
of electromagnetic energy available from the ionization energy
of helium.
- It is hard to get the repulsive protons close enough together to
let the strong force take over. You need very high temperatures
(T > 10^7 K) in order for strong collisions to cause these reactions
to happen. This is why this occurs in the very cores of stars that
are massive enough to be that hot!
- The reaction that supplies the energy for the Sun is:
4 H -> He
-
The main way of doing this is through the proton-proton
reaction. This occurs in 3 stages:
H + H -> D + e+ + v (x2 , 1.4 x 10^10 yrs)
H + D -> He3 + photon (x2 , 6 seconds)
H + He3 -> He + H + H (x1 , 10^6 yrs)
The funny things in the first reaction are a positron
(e+), which is the anti-electron and is just like an electron
but positively charged, and the neutrino (v), which is
a very light particle. Note that the first reaction is very
slow to happen, taking over 10 billion years on average. This
is because it turns a proton into a neutron (D is deuterium
a kind of hydrogen consisting of a proton and a neutron bound together)
using the weak force (hence the positron and neutrino).
The other reactions only use the strong force, and are easier.
- This reaction provides 90% of the Sun's energy. It requires
temperatures above 10 million K (10^7 K).
- Other Nuclear Reactions
- The CNO cycle (for Carbon - Nitrogen - Oxygen) also
turns 4 H -> He, but using carbon as a catalyst. This provides
about 10% of the energy of the Sun, and requires temperatures
of 16 million K.
- The Triple Alpha reaction turns 3 He -> C ("alpha particles"
are another term for the helium nucleus). This reaction needs
temperatures above 100 million K, and do not happen in the Sun
at this time. Later, however ...
- Carbon Fusion can occur above about 600 million K, and
produces oxygen, neon, magnesium and silicon. At still higher
temperatures around 3.5 billion K, silicon can be fused to form
heavier elements, including iron.
- The iron barrier: if you remember our consideration of
the binding energy per nucleon of the nucleus as a function
of the atomic weight of the nucleus, we showed that you could
extract energy from fusion only for elements lighter than
iron. Thus, iron is the "end of the line" for fusion as
an energy generator.
 Prev Lecture ---
Prev Lecture ---
 Next Lecture ---
Next Lecture ---
 Astr12 Index ---
Astr12 Index ---
 Astr12 Home
Astr12 Home
smyers@nrao.edu
Steven T. Myers
 Star Formation --- | ---
Stellar Evolution
Star Formation --- | ---
Stellar Evolution

 Star Formation --- | ---
Stellar Evolution
Star Formation --- | ---
Stellar Evolution

 Reading:
Reading: 


 Prev Lecture ---
Prev Lecture ---
 Next Lecture ---
Next Lecture ---
 Astr12 Index ---
Astr12 Index ---
 Astr12 Home
Astr12 Home