The Moon: an Introduction

The Moon, as viewed from the Earth, appears as a disk just over half a degree in diameter, approximately the same size as the Sun. The Moon is in an almost circular orbit around the Earth, but the variation due to the ellipticity is important as we shall see when we come to discuss solar eclipses. The sidereal period of the Moon's orbit is 27.322 days, the (average) time it takes for the moon the come back to the same place against the stars. Just like the solar day is longer than the sidereal day, the synodic period or the time between the same orientation with respect to the Sun, is also slightly longer than the sidereal day.

The Moon shines by reflected sunlight. The surface material of the Moon reflects back about 7% of the incident sunlight, and it is about 12% as reflective as if it were covered with opaque white paint. Because the Sun is very distant, at any given time only one hemisphere of the Moon is illuminated. As the moon orbits the Earth, we view this half-illuminated orb at different angles, thus causing us to see the varying phases of the Moon.

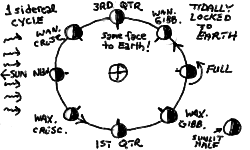
When the Moon is in the same direction in the sky as the Sun, we only see the dark hemisphere. This is known as the new moon. Conversely, when the Moon in its orbit is opposite the Sun relative to Earth, we see the sunlit hemisphere in full, thus the full moon. When the directions to the Sun and Moon from the Earth make a right angle, we see a "half-moon"; these are the first quarter and third quarter (so-called by their places in the lunar cycle). In between, we have waxing crescent and waning crescent just after and before the new moon, and waxing gibbous and waning gibbous just before and after the full moon. Here is a diagram of the phases:

These phases have been drawn from the perspective as if the Earth were stopped in its orbit about the Sun. This is approximately right, since the 27 days of the Moons orbit is much shorter than the 365 day period of the Earth's orbit. However, while the Moon revolves about the Earth to come back to the same sidereal orientation, the Earth has moved along in its orbit by the fraction 27.322 / 365.25, and the Moon is no longer in the same phase as it was the previous orbit! The Sun, in the meantime, has moved Eastward on the sky by 26.9 degrees (360 deg x 27.322 days / 365.25 days), at its usual solar yearly rate of 0.986 deg/day (360 deg / 365.35 days). The Moon also moves Eastward on the sky at the rate of 13.18 degrees/day ( 360 deg / 27.322 days). Thus, it can catch up to the Sun at the rate of 12.19 degrees per day ( 13.18 - 0.986). Therfore, to come to its same orientation with respect to the Sun and Earth, the Moon requires an extra 2.21 days ( 26.9 deg / 12.19 deg per day). Thus, the synodic period of the Moon should be 2.21 days longer than the sidereal period, or 29.53 days ( 27.32 days + 2.21 days ).

Like everything else in astronomy, the Earth - Moon - Sun system is more complicated than one might think. The orbital plane of the Moon is inclined by just over 5 degrees ( 5deg 8' 42") to the plane of the Earth's orbit about the Sun, the ecliptic. Thus, the Moon travels around the sky in a band within 5 degress of the ecliptic. Because of the gravitational interactions in the complicated Earth - Moon - Sun system, the axis of the Moon's orbit precesses about the ecliptic pole. The intersection of two inclined planes makes a line; for the plane of the Moon's orbit and the plane of the ecliptic, this line is called the line of nodes, and the directions on the sky of this line are the nodes (makes sense!). Thus, the line of nodes precesses around in the ecliptic plane with a period of 18.6 years.

Because of the 5 degree inclination of its orbit with respect to the ecliptic, plus the regressing line of nodes, the Moon will be found somewhere in the +/- 5 degree band about the ecliptic, between declinations 18 and 28 degrees north and south near the solstice points at 6h and 18h, and between -5 and 5 degrees at the equinoxes at RA 0h and 12h. If you were to plot the position of the Moon on the sky over the course of a few orbits, you would find that the orbit slips a little bit each cycle, as the nodes regress by 19.35 degress per year ( 360 deg/ 18.6 yrs ) along the ecliptic.

Tides

The tides raised upon the oceans (a poor choice of words as we will see) by the Moon are a complex and fascinating manifestation of the forces of gravity, rotational dynamics, the elasticity of the rock that makes up the Earth's crust, and fluid flow. And of course, if you live near or work on the high seas, a fact of life. The short version of the story is that the level of the ocean seems to rise and fall by a few feet twice each day, due to the inability of the solid earth to fully respond to the stresses induced by the Moon's gravitational influence.

Note what I did not say: that the Moon's gravity pulls the oceans up away from the Earth. The tides are not raised by the Moon, at least not directly. The tidal force caused by one body upon another is a stretching and compressing effect due to the differing strengths of the gravitational force being applied to parts of the "target body" (Earth) at different distances from the "originating" body (Moon). As we will see when we discuss Newton's theory of gravitation, the gravitational force from an object is proportional to the mass divided by the square of the distance, so stuff farther away feel less gravity. The point on the Earth nearest the Moon is 12800 km closer than the opposite point (the moon is roughly 384000 km from the center of the Earth). The difference in force between the closest and farthest parts of the Earth from the Moon tries to stretch the Earth along the line with the Moon (and to compress it in the perpendicular direction). The size of the effect is that the surface of the Earth should be stretched by about 60cm. Note that if the Earth were to do so, we would notice nothing, since the oceans would move outward like a thin skin on the surface. In physics-speak, the Earth will respond to the tidal force so as to remain in equilibrium between its own gravity and that of the Moon, and since we would remain in equilibrium we would only notice a very very slight change in our weight (the pull of Moon would slightly cancel the pull of the Earth when above us). This is hard to grasp in our gut, but it is so.

Why do we see the oceans seem to rise and fall? And why twice a day? It is because the Earth's rocky crust is stiff (try and stretch a rock!!!) and cannot move the full 60cm --- it is tidally stretched by only 20cm or so --- that the desired equilibrium is not reached. The uncancelled forces cause a horizontal flow of the water into the regions that should have been stretched, ie. the sub-lunar point (toward the moon) as well as the opposite side. Thus there are 2 equal places with respect to the moon where the flow causes the ocean level to rise, with a drop in between. Here is a sketch of this:

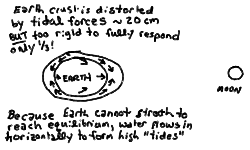
The rotation of the Earth carries a particular geographic point, say on the coast of New Jersey, through the "bulges" toward and away from the Moon. A good way of thinking about this is to note that since if the Earth were to stretch fully as the Moon's tidal force would like it to we would notice nothing, we can pretend that in this case the Earth were to remain spherical. The inability of the Earth to stretch all the way would then be like squashing the surface of the Earth along the Earth - Moon line down by 40cm, and watching the water flow along the surface into those regions. I don't think this an exactly correct analogue, but it is better than the confusing and incorrect explanation given by Seeds.

Tidal Friction and Length of Day

What goes around comes around. If the rather modest-sized Moon causes noticible tides on the much larger Earth, then we would expect the Earth to have a larger effect on the Moon. Indeed this is so, except the Moon has long since dealt with this problem by not moving its surface with respect to the Earth! This is the reason that the Moon keeps the same hemisphere toward the Earth during its orbit, with a rotational period equal to its orbital period. Over much of the 5 billion year history of the solar system, the relentless tidal force of the Earth has tidally locked the Moon's rotation into step with its orbit, so that there is no relative motion to cause frictional forces through changing stresses.

The same thing is happening to the Earth, though it has not had time to really affect things much since the tidal stress from the Moon is so much smaller. The friction induced by the stresses combined with the Earth's rotation relative to the Moon is slowing down the Earth's rotation by the tiny amount of 1.6 ms (or 1.6 x 10^-3 sec) per century! Thus, about 450 million years ago, the day was only 22 hours long. At this rate, it will take about 146 billion years to slow the Earth enough to lock with the Moon's orbit of 27 days.

Clarifications

Steven T. Myers - Last revised 03May96