An aperture synthesis telescope, like the GMRT, consists of a number of antennas located on the ground and the resolution of such a telescope is proportional to the maximum projected separation between the antennas. The locations of the antennas are usually specified in the Earth-centred XY Z co-ordinate system. The Earth centred XY Z frame is related to the xyz location of the antennas on the ground by
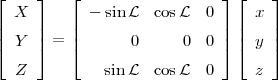 | (2.1) |
where 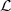 is the nominal latitude of the telescope site. The x-axis points towards the geographical
east, y-axis towards the north and z-axis towards the local zenith.
is the nominal latitude of the telescope site. The x-axis points towards the geographical
east, y-axis towards the north and z-axis towards the local zenith.
However, for the purpose of imaging, only the relative separation between the antennas is important. This separation between the antennas is usually referred to as the baseline and is measured in units of the wavelength λ of the incident radiation. For the purpose of the theory of synthesis imaging, the antenna positions are specified in the so called uvw frame. The geometric relationship between this XY Z frame and the uvw frame is shown in Fig. 2.1 and the co-ordinate transformation is given by
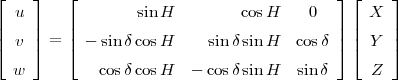 | (2.2) |
where H is the Hour Angle and δ the declination of the source.
The geometric relation between the observing plane represented by the uv-plane and the sky plane represented by the lm-plane is shown in Fig. 2.2. The lm-plane in the sky is parallel to the plane in which measurements are made (the uv-plane) and the separation between them is denoted by R. The w-axis points towards the origin of the lmn frame given by (l = 0,m = 0) and is parallel to the n-axis. The treatment of the theory of synthesis imaging given below follows that of Thompson et al. (1986) and Clark (1999).
Let E(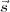 ,
,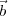 1,t) represent the electric field produced by an infinitesimal element in the sky in the
direction
1,t) represent the electric field produced by an infinitesimal element in the sky in the
direction 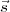 at point
at point 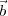 1 in the uvw frame (Fig. 2.2). The total electric field e(
1 in the uvw frame (Fig. 2.2). The total electric field e(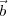 1,t) measured at
this point will be an integral of the signals from all the radiation elements and is given
by
1,t) measured at
this point will be an integral of the signals from all the radiation elements and is given
by
|
|
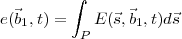 | (2.3) |
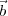 1 is the vector denoting the point 1 in the uvw frame. Let R1 be the distance between point
1 is the vector denoting the point 1 in the uvw frame. Let R1 be the distance between point 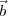 1
and the point in the source plane towards the direction given by the vector
1
and the point in the source plane towards the direction given by the vector 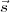 1. E(
1. E( 1,
1, 1,t) can
then be written as
1,t) can
then be written as
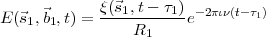 | (2.4) |
where ξ is the complex amplitude of the radiation at the source, ν is the frequency of the radiation, τ1 = R1∕c and c is the speed of light. τ1 represents the propagation delay for the radiation of complex amplitude ξ to travel the distance R1.
The source coherence function, defined as
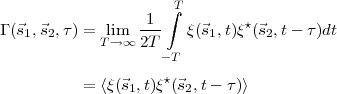 | (2.5) |
is a measure of the coherence between radiation from two points on the source given by the
directions 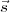 1 and
1 and 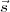 2 respectively. For a spatially incoherent source, radiation from two points on
the source will be uncorrelated. For such a source, Γ(
2 respectively. For a spatially incoherent source, radiation from two points on
the source will be uncorrelated. For such a source, Γ(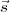 1,
1,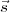 2,τ) = δ(
2,τ) = δ( 1 -
1 - 2) and equation 2.5 can
be written as
2) and equation 2.5 can
be written as
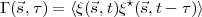 | (2.6) |
This is the auto-correlation function of the radiation from the source Γ(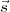 ,0) is a measure of the
average surface brightness of the radiation from the source.
,0) is a measure of the
average surface brightness of the radiation from the source.
The mutual coherence function, measured at two points 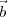 1 and
1 and 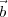 2 on the observing plane is
defined as
2 on the observing plane is
defined as
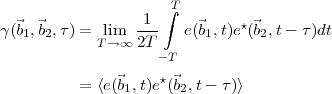 | (2.7) |
Using Equations 2.3 and 2.4 and the equivalent equations for the point 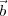 2, the above equation can
be written as
2, the above equation can
be written as
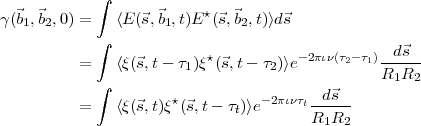 | (2.8) |
where τt = τ2 - τ1 = (R2 - R1)∕c is the relative delay between the signals measured at the
points 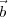 1 and
1 and 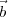 2 respectively.
2 respectively.
In the above equation, the dependence on 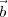 1 and
1 and 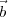 2 is implicitly via τt. For a plane wavefront
from a direction
2 is implicitly via τt. For a plane wavefront
from a direction 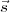 in the sky, τt =
in the sky, τt = 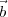 12 ⋅
12 ⋅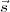 ∕c where
∕c where 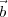 12 is the vector separating the two antennas. It
is therefore clear that γ depends only on the relative separation between the antenna positions
given by
12 is the vector separating the two antennas. It
is therefore clear that γ depends only on the relative separation between the antenna positions
given by 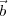 1 and
1 and 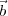 2 and can be written as
2 and can be written as
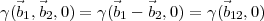 | (2.9) |
The components of 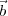 12 will be given by (u12,v12,w12)=(u2 -u1,v2 -v1,w2 -w1). Using direction
cosines of
12 will be given by (u12,v12,w12)=(u2 -u1,v2 -v1,w2 -w1). Using direction
cosines of 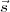 as the (l,m,n) co-ordinates of a point in the sky, we get
as the (l,m,n) co-ordinates of a point in the sky, we get
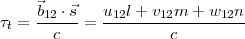 | (2.10) |
Let the antenna located at point 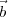 1 track a direction given by the unit vector
1 track a direction given by the unit vector 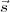 in the sky. Due to
the separation between the antennas on the ground, to track the same point in the sky, a second
antenna located at point
in the sky. Due to
the separation between the antennas on the ground, to track the same point in the sky, a second
antenna located at point 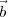 2 will need to point in a slightly different direction given by
2 will need to point in a slightly different direction given by 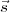 2. The
angle between
2. The
angle between 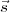 and
and 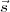 2 is given by tan-1(|
2 is given by tan-1(|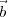 2 -
2 -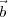 1|∕R). This difference in the pointing directions
results in an extra relative delay between the signal arriving at the two antennas from a point in
the sky. As a result, one of the antennas samples a slightly delayed version of the wave front. If,
however, R ≫|
1|∕R). This difference in the pointing directions
results in an extra relative delay between the signal arriving at the two antennas from a point in
the sky. As a result, one of the antennas samples a slightly delayed version of the wave front. If,
however, R ≫|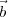 2 -
2 -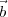 1|∕λ where λ is the wavelength of the radiation, the same wavefront will
be sampled by the two antennas (tan-1(|
1|∕λ where λ is the wavelength of the radiation, the same wavefront will
be sampled by the two antennas (tan-1(|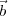 2 -
2 -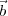 1|∕R) ≈ 0). This corresponds to the
usual plane wavefront approximation. This approximation is used in the rest of the
treatment.
1|∕R) ≈ 0). This corresponds to the
usual plane wavefront approximation. This approximation is used in the rest of the
treatment.
In the limit of the plane wave front approximation, the denominator in Equation 2.8 can be
adequately represented by R2 and d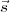 ∕R2 = dldm∕
∕R2 = dldm∕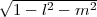 . The phase of the mutual
coherence function in Equation 2.7, for a spatially incoherent source, therefore, depends only
on the relative separation between the points of measurement in the far field of the
radiation.
. The phase of the mutual
coherence function in Equation 2.7, for a spatially incoherent source, therefore, depends only
on the relative separation between the points of measurement in the far field of the
radiation.
Let 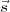 ∘ represent the unit vector along the w-axis pointing towards (l = 0,m = 0). The
components of
∘ represent the unit vector along the w-axis pointing towards (l = 0,m = 0). The
components of 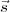 ∘ in the uvw frame will be (0,0,1). The relative delay between the signals received
at the two antennas from a point source in this direction will be τg =
∘ in the uvw frame will be (0,0,1). The relative delay between the signals received
at the two antennas from a point source in this direction will be τg = 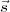 ∘⋅
∘⋅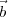 12∕c = w12∕c. Treating
12∕c = w12∕c. Treating
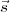 ∘ as the reference direction towards the origin of the source co-ordinate system, the
instantaneous phase of γ(
∘ as the reference direction towards the origin of the source co-ordinate system, the
instantaneous phase of γ(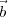 12) can be measured with respect to this direction, without losing any
information about the sky brightness distribution. This can be done by rotating the phase of γ by
-2πνw12∕c. The point in the sky in the direction
12) can be measured with respect to this direction, without losing any
information about the sky brightness distribution. This can be done by rotating the phase of γ by
-2πνw12∕c. The point in the sky in the direction 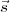 ∘ is referred to as the phase centre and τg is
referred to as the geometrical delay. The Phase centre direction defines the origin of the source
co-ordinate system. Since
∘ is referred to as the phase centre and τg is
referred to as the geometrical delay. The Phase centre direction defines the origin of the source
co-ordinate system. Since 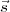 ∘ is an arbitrary vector, the phase centre can be chosen at
any convenient point in the sky. Usually, this is coincident with the antenna pointing
centre.
∘ is an arbitrary vector, the phase centre can be chosen at
any convenient point in the sky. Usually, this is coincident with the antenna pointing
centre.
The visibility phase for a point source at the phase centre, after correcting for the geometrical phase is equal to zero. With this correction, the visibility is said to be ‘phased’ for the phase centre. An interferometer phased for this reference direction will remain phased for all points on the surface of a sphere of unit radius passing through the point (l = 0,m = 0), centred at (u = 0,v = 0) and described by the equation l2 + m2 + n2 = 1. Under ideal conditions (i.e., with no other source of phase errors), any residual phase would be due to the relative separation between the phase centre and a source of emission located on such a sphere. In that sense, the visibility phase from a ‘phased’ interferometer provides information about the distribution of the sky brightness, relative to the phase centre. Moving one of the antennas to the origin of the uvw frame, the (u12,v12,w12) co-ordinates are just the co-ordinates of the other antenna and the subscript ‘12’ can be dropped from Equation 2.10.
The length of time for which a signal remains coherent is given by the inverse of the
bandwidth Δν. After correcting for the geometrical delay, the relative delay between the signals is
τc = τt -τg. Replacing τt by τc in Equation 2.8 corresponds to the geometrical delay corrected
version of this equation. If τc ≪ Δν-1, two versions of a time series displaced with respect
to each other in time by τc will remain coherent. In the limit of the validity of the
assumption that τc ≪ Δν-1, ⟨ξ(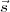 ,t)ξ⋆(
,t)ξ⋆(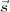 ,t - τc)⟩ in Equation 2.8 can be replaced by
⟨ξ(
,t - τc)⟩ in Equation 2.8 can be replaced by
⟨ξ(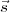 ,t)ξ⋆(
,t)ξ⋆(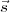 ,t)⟩ = ⟨|ξ(
,t)⟩ = ⟨|ξ(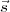 )|2⟩. This is the same as the source auto-correlation function at zero lag,
Γ(
)|2⟩. This is the same as the source auto-correlation function at zero lag,
Γ(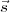 ,0) (Equation 2.6) and is equal to the two dimensional source surface brightness, denoted by
I(l,m)
,0) (Equation 2.6) and is equal to the two dimensional source surface brightness, denoted by
I(l,m)
Therefore, under the approximation that:
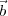 2 -
2 -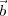 1|∕λ)
1|∕λ)
using the relation between l,m,n in Equation 2.10 and the above mentioned phase rotation, Equation 2.8 can be re-written as
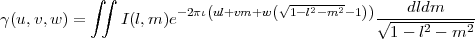 | (2.11) |
where u, v and w are now the co-ordinates in the uvw frame measured in units of the wavelength. γ is usually referred to as the visibility function and denoted by V (u,v,w).
The integrals in the above equation are over the entire sky (limits of the integral from -1 to 1). However, the antenna primary beam limits the part of the sky from which the antenna can receive radiation to ~ λ∕D, where D is the diameter of a circular aperture. Assuming that the response close to the centre of the primary beam is ≈ 1, with an additional approximation that the field of view is small (l2 + m2 ≪ 1), Equation 2.11 can be written as
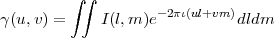 | (2.12) |
This is a 2D Fourier transform relation between the mutual coherence function (visibility) and the source surface brightness. This statement is referred to as the van Cittert-Zernike theorem (Born & Wolf 1959 [and later eds]; Thompson et al. 1986) and forms the basis of imaging with interferometric radio telescopes.
The source surface brightness I(l,m) is described in the lm-plane while u and v are the equivalent conjugate variables in Fourier space. u and v can therefore be interpreted as the spatial frequencies and the visibility function as the spatial frequency spectrum of the source surface brightness distribution. Synthesis radio telescopes like the GMRT measure the visibility function at several points in the uvw frame using an array of N antennas which instantaneously produce N(N - 1)∕2 pairs of interferometers. Due to the rotation of the earth, the projected separations between the antennas change as the antennas track a source in the sky. Over time, each antenna pair therefore measures the visibility at several points in the uvw frame. As a result, over time, the array of antennas partially covers the uvw volume, up to a maximum projected antenna separation of Bmax corresponding to a spatial resolution of 1∕Bmax. Also, an interferometric array does not measure V for baselines smaller than a minimum value. Just as the maximum baseline length for which V is measured corresponds to the highest spatial resolution the telescope can provide, the smallest baseline for which V is measured corresponds to largest angular scale that can be represented reliably in the final image. Hence, an interferometric observation will be insensitive to scales larger than 1∕Bmin; this problem of missing short spacing measurements is referred to as the problem of “missing short spacing”. When imaging extended objects in the sky, like the ones imaged for this dissertation, the shortest spacing for which a reliable measurement exist has for reaching implications – missing short spacings result in missing extended emission in the image.
If γ(u,v) is completely sampled, at least at the Nyquist rate, it can be inverse Fourier transformed to recover the source brightness distribution I(l,m). With a finite number of antennas located at discrete locations on the ground, the visibility function is sampled at a discreet set of points. The observed visibility can, therefore, be thought of as the true visibility, multiplied by the sampling function given by
 | (2.13) |
where (u(t),v(t)) represents the points sampled at time t. Using the convolution theorem for Fourier transform (Bracewell 1986 [and later eds]), it can be shown that the function I, recovered by the inverse Fourier transform of S(u,v)γ(u,v), will be convolved by the inverse Fourier transform of S. The inverse Fourier transform of S, denoted by B, is usually referred to as the dirty beam or the point spread function or the telescope transfer function. Id = I ⋆B is referred to as the dirty map, where ‘⋆’ represents the convolution operator. I is recovered from Id using non-linear deconvolution techniques (Högbom 1974; Clark 1980; Cornwell & Evans 1985).
The approximation that l2 + m2 ≪ 1 breaks down at low frequencies and Equation 2.11 accurately described the measured visibility function. However, this is not a Fourier transform relation. Techniques used to recover I in such cases are described in Chapter 4.
|
|
In practice, γ is measured by a number of two element interferometers, one of which is shown in
Fig. 2.3. The signal from antenna 1 lags behind the signal from the antenna 2 by a phase equal
to 2πb12⋅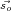 c where
c where 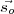 is the reference unit vector mentioned in the previous section.
Under the plane wave approximation, the signals from the two antennas can be written
as
is the reference unit vector mentioned in the previous section.
Under the plane wave approximation, the signals from the two antennas can be written
as
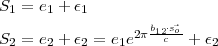 | (2.14) |
where ϵ1 and ϵ2 are independent additive random noises from the two antennas. These signals are multiplied and the product averaged in the complex correlator to form the visibilities as
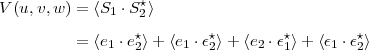 | (2.15) |
Since ϵ1 and ϵ2 are independent zero mean gaussian random variables, the last three terms will reduce to zero.
The response of the interferometer to a point source of flux density I, located at the phase centre (l = 0,m = 0) is therefore
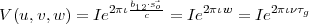 | (2.16) |
where τg is the geometrical delay mentioned earlier. It is equal to the time delay due to the extra
path length (equal to the projected separation between the antennas along 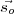 ) which the radiation
has to travel to reach one of the antennas. With reference to Fig. 2.3, ντg = D
λ sin(θ) = wλ where
D = |
) which the radiation
has to travel to reach one of the antennas. With reference to Fig. 2.3, ντg = D
λ sin(θ) = wλ where
D = |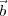 12| and wλ is the instantaneous component of the separation between the antennas along
the w-axis measured in units of the wavelength of the incident radiation. Equation 2.16 can
therefore be rewritten as
12| and wλ is the instantaneous component of the separation between the antennas along
the w-axis measured in units of the wavelength of the incident radiation. Equation 2.16 can
therefore be rewritten as
Antennas receive radiation from a finite part of the sky, defined by the antenna primary beam. For an extended source, within the antenna primary beam, V (u,v,w) will be an integral over the source (integral over l and m;Equation 2.12) and can be thought of as a superposition of plane waves from the individual infinitesimal elements constituting the extended source given by Equation 2.17.
As the interferometer tracks the source in the sky, the projected separation and hence the geometrical delay changes with time. θ changes slowly going from -θmax to θmax when the antennas track a source from rise to set over several hours. θmax depends on the declination of the source and the minimum elevation limits of the antennas. Over short intervals of time, θ changes almost linearly with time. The interferometer response to a point source (the real and imaginary parts) therefore varies quasi-sinusoidally over short periods of time with a frequency proportional to the separation between the antennas. This quasi-sinusoidal variation of the interferometer output, due to the changing geometrical delay, is referred to as the fringe pattern. The amplitude of this fringe pattern is directly proportional to the power emitted by the source in the sky. The phase of these fringes also changes sinusoidally with time with a period of 24 hours. The phase of this fringe pattern due to the geometrical delay however carries no astronomically useful information about the sky (it only carries information about the direction in the sky being tracked). In practice therefore, the geometrical delay is continuously compensated by introducing a time variable compensating delay τi in the signal from one of the antennas. This operations is referred to as delay tracking. The radio-frequency (RF) signals from the antenna feeds, centred at a frequency νRF ∘, are converted to an intermediate frequency band centred at νIF ∘ to be transported to the correlator (in the case of GMRT, over optical fiber cables). The path length for the signals from the antenna to the correlator introduces a time invariant fixed delay τFix suffered by the signals at νIF . The compensating delay τi must therefore compensate for τFix as well.
For the GMRT, the compensating delay τi = τg + τFix is applied to the signals at baseband frequencies in the correlator. However, the signals suffer the delays τg and τFix at the RF and IF frequencies respectively. Delay compensation at the baseband therefore leaves a residual phase given by
![Δϕ-= [τgν∘RF + τFixν∘IF]+ [(τg + τFix - τInt)νi]
2π
≡ Δϕ-∘+ Δϕi-
2π 2π](thesis125x.png) | (2.18) |
where νi is the centre frequency of the ith frequency channel and τInt is the time delay, applied in the correlator Delay/DPC system (see 2.5.2 for details). This delay compensated signal is fed to the FFT section of the correlator to be split into a number of frequency channels. Δϕ∘ is applied at the very first stage of the FFT butterfly network in the FFT section. The remaining phase gradient, denoted by Δϕi, is applied as a phase gradient in the last stage of the FFT network.
Effectively, the phase of the visibilities is rotated by Δϕ, equivalent to the residual delay due to the differences in the RF, IF and base band frequencies. The phase of the visibility for a point source located at the phase centre is thus reduced to zero at all times. This final rotation of the fringe phase is referred to as fringe stopping or fringe rotation.
Note that the total phase applied to the visibilities via delay tracking and fringe rotation is equal to 2πw and this effectively phases the interferometer for a point in the sky (the phase centre). Application of this total phase is achieved in the GMRT correlator in two stages, as explained in Section 2.5.2.
The response of the interferometer is integrated over the signal bandwidth as seen by the multiplier in the correlator. If H(ν) represents the voltage response of the antennas as seen by the multiplier, the effect of a finite bandwidth is to modulate the output of the interferometer by the Fourier transform of H. If the receiver has a flat response for a range of frequencies νo ± Δν, the output V , for a source of unit flux density, will be given by
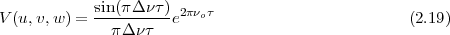
w is the relative antenna separation along the w-axis. As is clear from Equation 2.2, the geometrical delay involves the measurement of the relative (X,Y,Z) co-ordinates of different antennas. It is therefore important to measure the relative antenna co-ordinates as well as the fixed delays for phasing the array (reducing the fringe phase to zero for the phase centre). The procedure used for measuring the relative antenna co-ordinates (referred to as baseline calibration) and fixed delays (referred to as fixed delay calibration) for the GMRT is described in Sections 2.6.1 and 2.6.2 respectively.
As mentioned earlier, V (u,v,w) is measured for several values of u,v and w by tracking the source in the sky for several hours, during which the projected baseline of a single interferometer changes with time. In practice, a number of antennas are used and the output of all the N(N - 1)∕2 interferometer pairs made by an array of N antennas provide instantaneous measurements at several values of u,v and w. The instantaneous set of points measured in the uvw frame by an array of antennas is referred to as the snapshot uv-coverage. As the array tracks a source in the sky, each interferometer generates a track in the uv-plane, dramatically increasing the uv-coverage of the array. The set of u,v,w points, measured by an array of antennas over several hours of source tracking, is referred to as the full synthesis uv-coverage. The shape and density of the uv-coverage of the array determines the telescope transfer function and the geometry of the array is usually optimized to maximize the uv-coverage (Mathur 1969). The configuration of the 30-antenna GMRT array and resulting uv-coverage are described in Section 2.2.
The GMRT antennas are fully steerable parabolic dishes each of 45m diameter each with an Alt-azimuth mount. A turret at the prime focus of the antenna is supported by a quadripod and holds a sealed metallic cube which houses the broadband low noise amplifier (LNA), RF filters, the polarizer and the RF switch for swapping the polarization channels for each RF band (see Section 2.3). The feeds for 150, 327, 233/610, and 1420 MHz are mounted on the four faces of the turret which can be rotated to bring the desired feed in focus using the feed positioning system (FPS). The feed bandwidths and the range of frequencies covered by the various feeds are listed in Table 2.1. The feed bandwidths correspond to a Standing wave ratio of ≤ 2. The 233-MHz feed has the smallest bandwidth while the cross-polar characteristic of the 150-MHz feed is the worst. The measured cross-polar power at 327 and 610 MHz bands is ~-42 and ~-47 dB respectively while that for the 150-MHz feed is ~-22 dB. The value away from the centre of the radiation pattern is ~-22 dB for 327 and 610 MHz bands while that for the 150-MHz feed is ~-20 dB (see Sankar (2000) for more details). Since the GMRT is predominantly a low frequency instrument, the reflecting surface of the antennas is a light weight wire mesh. The wire mesh is held in place by a network of steel ropes, creating patches of flat surfaces which approximate a parabola. This design is referred to as the Stretched Mesh Attached to Rope Trusses design or the SMART design (Swarup et al. 1991). Three sizes of wire mesh are used, going from smallest sized mesh (10 mm) in the inner region of the parabola to the largest size (20 mm) towards the edge to produce a tapered illumination pattern which reduces the side-lobe levels of the antenna radiation pattern. Mesh of different sizes each covers one third of the total surface area. The reflecting surface for each antenna was measured by theodolite, to determine the surface accuracy compared to an ideal parabola. An RMS deviation of 8, 9 and 14 mm from an ideal parabola was measured for the three regions of the surface (Sankar 2000).
|
|
|
|
|
|
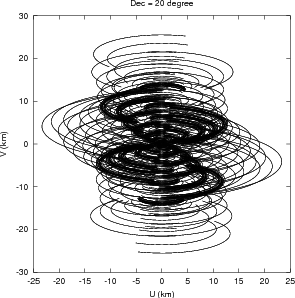
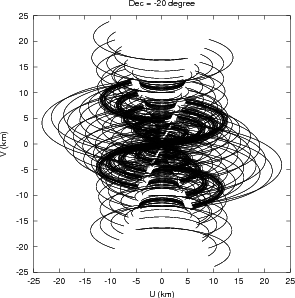
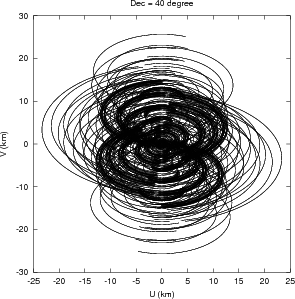
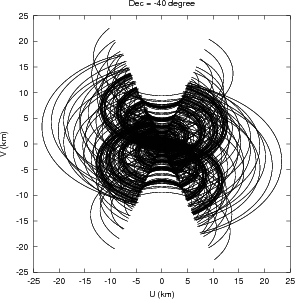
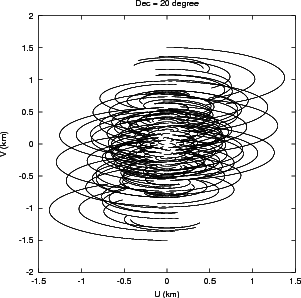
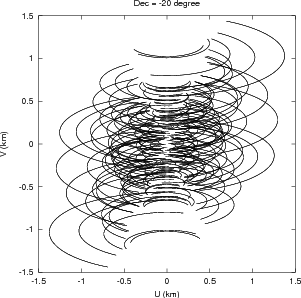
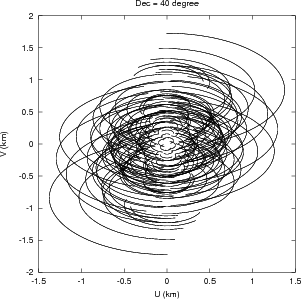
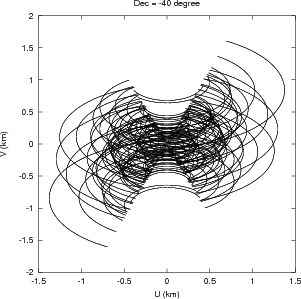
The GMRT is composed of 30 such antennas. The antennas are located in a roughly ‘Y’ shaped geometry (Mathur 1969), as shown in Fig. 2.4. Fourteen antennas are located randomly in a region of size ≈ 1 km×1 km, referred to as the Central Square (see Fig. 2.5). These antennas provide the short spacing coverage of the uv-plane, which is essential for mapping large scale structures. The rest of the antennas are located in ~ 14 km long Western-, Eastern-, and Southern-arms. The Eastern- and Southern-arms each have 5 antennas, roughly along a straight line, while the Western-arm has 6 antennas. This arrangement of antennas was designed to maximize the telescope sensitivity to large scale emission as well as to provide high resolution. The shortest spacing of ~ 60 m in the Central Square is provided by the antennas C05, C06 and C09 while the largest spacing of ~ 25 km is provided by the arm antennas. The Central Square antennas together provide a uv-coverage up to 1 km. The uv-coverage for a full 12h synthesis observation using the full array is shown in Fig. 2.6. The uv-coverage due to Central Square antennas alone, for a full 12h synthesis at a few declinations is shown in Fig. 2.7.
A detailed description and analysis of the analog signal flow for the GMRT has been described elsewhere (Praveen Kumar & Srinivas 1996; Praveen Kumar 2000). This section briefly describes the aspects of the GMRT analog receivers which are relevant from the point of view of astronomical observations.
The GMRT operates at the 150, 233, 327, 610 and L-band extending from 1000 - 1450 MHz. The L-band is split into four sub-bands centred at 1060, 1170, 1280 and 1390 MHz with a bandwidth of 120 MHz while the bandwidth at other bands is ~ 40 MHz. Fig. 2.8 shows a simplified schematic diagram, with the major components of
|
|
the GMRT receiver. The L-band feeds measure two orthogonal linear polarizations while the feeds at all other bands measure circular polarizations. The 233 and 610 MHz feeds are co-axial feeds. The front-end low noise amplifiers have been designed to either receive two polarization signals from a single feed or the same polarization signal from two different feeds. This, for the case of 233/610 MHz feeds, allows simultaneous single polarization observations at these bands. An RF switch after the front-end box allows swapping of the two polarizations signals. Solar attenuators of 14, 30 and 44 dB are also available. Four calibrated noise sources, named Low, Medium, High and Extra-high cal can be used to calibrate the receiver system. However, the planned periodic injection of calibrated noise has not yet been implemented. The Front-end electronics also has the facility for Walsh switching of the two polarization channels using orthogonal Walsh functions to minimize polarization leakage. However this is also not yet operational at the GMRT.
The RF band is first converted to an IF band centred at 70 MHz using what is referred to as the First LO (First Local Oscillator). Here, bandwidths of 5.5, 16 or the full RF bandwidths can be selected. The two IF signals corresponding to the two polarizations are then converted to 130 and 175 MHz with a maximum bandwidth of 32 MHz using the Second LO. These signals are then transported over optical fibers to the Central Electronics Building (CEB). Variable attenuators in the range of 0 - 30 dB, which can be varied in steps of 2 dB are available separately for the two IF signals. An automatic level controller (ALC) at the output of the IF can be bypassed if required (e.g. for observations requiring measurement of variations at high time resolution). At the CEB, the 130- and 175-MHz signals, recovered from the output of the optical fibers, are fed to the Base Band system for conversion to base-band signals. These signals are first converted to 70 MHz band and then split into Upper- and Lower-Sidebands using the tunable Fourth LO. This LO can be tuned between 50 - 90 MHz in steps of 100 Hz. At the base band, bandwidths of the 62.5, 125, 250, 500 KHz or 1, 2, 4, 8, 16 MHz can be selected. Another ALC is provided at the output of the baseband. Signal levels are kept at 0 dBm by this ALC before being fed to the correlator (see Section 2.5). This ALC also can, however, be bypassed.
For the purpose of astronomical observations, settings of the attenuators and the First and Fourth LOs are important. The combination of these two LOs determine the exact RF frequency used for observations.
The output of the individual antennas is a random signal composed of the signals from the source of interest in the sky, the sky background emission and the thermal noise generated by the various electronic components through which the signal flows. The output of the antennas and the receiver is usually expressed in terms of the temperature of a blackbody which will emit equivalent power. The system temperature (Tsys) of an antenna at a particular frequency, is equivalent to the total power from the antenna when it points towards a blank sky. The power received by an antenna due to the celestial source alone is represented by the antenna temperature (Ta).
The normalized visibility amplitude from antennas 1 and 2 is given by
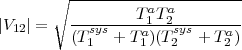 | (2.20) |
where Tsys = Tr + Tbg + Tspill, Tr is the receiver temperature, Tbg is the temperature of the sky background emission, and Tspill is antenna spill-over temperature. An unpolarized point source of flux density S (in units of Wm-2Hz-1) will result in Ta = AeS∕2k = ηS where Ae is the effective collecting area of the antenna, k is the Boltzman’s constant and η is the antenna sensitivity. For identical antennas and for the range of S where Ta ≪ Tsys, |V 12|≈ Ta∕Tsys ∝ S. Tr, Tsys and η are therefore important telescope parameters, which together determine the sensitivity of the telescope.
These and other astronomically relevant parameters of the GMRT are listed in Table 2.21 . Fifth column is listed the angular resolution for both Central Square and full array.
|
The prototype 4 and 8 antenna correlator, all of the initial design and most of the implementation of the final 30 antenna single sideband correlator currently in use and which was used for the observations for this dissertation were designed and built by the team consisting of C.R.Subramanya, A.Dutta, V.M.Tatke, A.Dikshit, R.K.Malik, U.Puranik, M.Burse and others. Further development for the second sideband correlator and maintenance is now done by Y.Gupta, M.Burse, S.Sirothia, C.P.Kanade, K.H.Dahimiwal, I.Halagalli and others, with contributions from A.Roshi. This section describes aspects of the GMRT correlator relevant from the point of view of astronomical observations. A more detailed description of the current correlator hardware design is given by Tatke (1998). The correlator control and data acquisition software for potentially multiple sub-array mode of operation was designed and implemented by R.K.Singh and C.R.Subrahmanya. A detailed description of the current correlator control and data acquisition software is given by Singh (2000). The sub-array mode of operation is described by Chengalur (2000).
The GMRT back-end for interferometric observations is an FX-type digital correlator. The block diagram in Fig. 2.9 shows the various stages of the correlator. The first stage of this correlator consists of a set of four samplers per antenna - one for each of the two IFs per side-band of the antenna. Each antenna produces two IFs which can carry either the two orthogonal polarization signals or the same polarization from two different RF bands (as in the case of 233∕610 MHz dual frequency feed). The analog to digital converter (ADC) of the samplers converts the input analog signal to 8-bit unsigned numbers. These 8-bit samples are converted to 6-bit unsigned numbers before being fed to the next stage of the correlator, referred to as the Delay and Data Preparation Cards, or the Delay/DPC system. These samples are further converted to 4-bit signed numbers in the Delay/DPC system (see the section on Samplers below), before being fed to the next stage of the correlator. This conversion from 8-bit to 4-bit samples is required since the VLBA FFT chips used in the correlator work with 4-bit signed numbers. Part of the compensating delay equivalent to integral units of correlator clock is applied in the Delay/DPC stage. Any residual delay (corresponding to a fraction of the correlator clock) is applied as a phase ramp across the band, after the signals have been Fourier transformed (see Section 2.5.2). The Delay/DPC stage is followed by the Fast Fourier Transform or the FFT stage which performs a 512-point FFT corresponding to 256 point complex spectra (the other 256 points being the complex conjugate spectra). The output complex numbers are represented in 4,4,4-bit format consisting of two 4-bit numbers for the mantissa of the real and imaginary parts and a common 4-bit exponent.
|
|
The correlation between signals from two antennas with the same polarization is referred to as the co-polar visibilities. This correlation is done by multiplying the antenna signals and averaging the result in the correlator. The output of the FFT stage is therefore fed to the Multiplier and Accumulation (MAC) stage of the correlator. Each MAC chip accepts 4 input data streams – 2 IFs from the two antennas. However each MAC can only handle a total of 256 channels per antenna. Therefore, either the number of channels per IF must be reduced from 256 to 128 or, only one IF with all the 256 channels must be fed to the MAC. This reduction of 256 channels for each IF to 128 channels to produce the co-polar visibilities is done by averaging two adjacent frequency channels. However, the GMRT correlator can also be used with a resolution of 256 frequency channels by sacrificing one of the polarization signals from the antennas.
The MAC output format consists of two 15-bit mantissa for real and imaginary parts and a common 6-bit exponent (this format is referred to as 15,15,6-bit format). The accumulators in the MAC stage provide the Short Term Accumulation (STA). Each STA cycle corresponds to 512 correlator clock cycles, required for reading the 512 points into the FFT section plus 4 clock cycles required to set-up the FFT cards before it can perform an FFT. Thus, each FFT cycle requires 516 correlator clock cycles. The correlator runs on an effective clock of 32 MHz and the STA accumulates the data for 4096 FFT cycles. Thus, the STA corresponds to an integration of (512 + 4) * 4096∕(32MHz) = 66 ms of time. (Strictly speaking, the samplers run on a 32 MHz clock. This is the shortest time resolution that the GMRT correlator can provide. The Delay/DPC system reads the input data at the rate of 32 MHz but output data rate is 32.125 MHz. The rest of the correlator operates at 32.125 MHz to effectively take care of the dead time corresponding to the 4 clock cycles required for FFT setup).
The data rates corresponding to a STA time interval is large (8 MBytes/sec) and difficult to sustain for any data recording system. The STA data therefore needs to be integrated further to reduce the data rate by accumulating in the Long Term Accumulation (LTA) stage of the correlator. This stage has not yet been implemented in the hardware and therefore, the STA stage has been set to integrate for 8192 FFT cycles corresponding to a minimum integration time of 132 ms. This brings down the data rates to 4 MBytes/sec and the data is further integrated in the software for an integration time than can be set by the user to produce the final LTA data. The output of the STA stage is the final product of the correlator and is produced in the form of three data streams from the three MAC racks per sideband.
All the three MAC output streams are fed to the Data Acquisition System (DAS), via a 16-bit bus. The DAS consists of a dual CPU PC running under the GNU/Linux Operating System (OS) with a data acquisition card on its PCI bus. The STA data from all MACs is acquired on this card at the rate of 4 MBytes/sec consisting of all the 256 channels (256 frequency channels with only one polarization, or 128 channels with both polarizations). The software device driver (which runs in the kernel space of the OS) and the supporting program (running in the user space of the OS) convert the input complex numbers from the correlator representation to the IEEE floating point representation. The software LTA is done at this stage for a time interval set by the user and the data rate further reduced. Through a series of network software, this data is transfered to another machine over the fast Ethernet to be recorded on the disk in what is referred to as the LTA-format (Singh (2000)). The last stage in the chain of software also provide facilities for further integration in time and frequency and for defining sub-arrays, etc. (the usage of the sub-array mode of the software is described by Chengalur (2000)).
The analog-to-digital converter (ADC) used in the GMRT samplers is an 8-bit flash ADC (Tatke 1998). The input to these samplers is the band limited gaussian random noise from the antennas, converted to base-band (BB) (corresponding to a frequency range of 0 to 16 MHz). The output power of the baseband system is proportional to the antenna temperature which is a function of the sky temperature. The sky temperature, can vary by as much as a factor of 4 - 5 between the Galactic plane and away from it. However, the samplers are designed to sample a fixed range of input signal. The BB output signals are therefore maintained at 0 dbm by the Automatic Level Controller (ALC) before being fed to the samplers. This corresponds to a peak-to-peak variation of ±1 V spanning the input random signal up to the six sigma level. In order to preserve the statistical properties of the input, the 28 comparator voltage levels (in the ADC) must be optimally set such that the samplers neither saturate when the input voltage deviates by six sigma from the mean, nor sample the weaker signals too coarsely (corresponding to much smaller deviations from the mean). As of now, the 28 voltage levels corresponding to 8-bit sampling are uniformly distributed across this range of voltage, corresponding to a voltage resolution of 7.8 mV (provisions however exist for a more sophisticated scheme to distribute the levels across the range of input signal). However, before being fed to the next stage of the correlator (namely the Delay/DPC stage), the 8-bits samples are converted to 6-bit samples by dropping the 2 least significant bits (LSB) of the samples. Effectively, this corresponds to 26 levels covering the full range of ±1 V, with a resolution of 31.25 mV, but which still sample the full range of the input signal up to six sigma, although at a coarser resolution. These 6-bit samples are unsigned. Inside the Delay/DPC system these samples are further converted to 4-bit signed values via a look-up table. The look-up table is made such that the 24 levels are again uniformly distributed for the entire range of the input signal (in this case, the 6-bit samples). Hence, effectively, the input signal with 6-bit resolution is further sampled at a coarser resolution of 4-bits without statistically altering the signal.
For the purpose of astronomical observations, this entire operation of converting the 8-bit unsigned samples to 4-bit signed samples can be ignored and the GMRT samplers can be treated as an effective 4-bit samplers.
This section describes the mechanisms used in the correlator data acquisition software for deriving accurate time information. This is essentially a description of the work done by Singh (2000).
The input data to the DAS is averaged for a length of time set by the user to produce the long term accumulated (LTA) data. This interval is typically set to 10 - 20 sec. The LTA operation is currently done in the software and may be moved to hardware in future (if required).
As mentioned earlier, a synthesis radio telescope like the GMRT utilizes the earth rotation to synthesize an effective large aperture. To keep the array instantaneously phased, the time varying geometrical delay must be continually compensated. The phasing of the array is therefore a time critical operation requiring accurate time keeping. Accurate time information is also required for proper pointing of the antennas and tracking of an astronomical source. Stamping of astronomical data with accurate time is therefore very important.
Absolute time for the GMRT is kept using the real time clock (RTC) of the GMRT correlator control computer. This clock is synchronized with the GPS time using a GPS receiver. The GPS and correlator system clocks are used to remove any time jumps and/or slow drifts of this real time computer clock as described below. This time stamping of the visibility data in the GMRT correlator/data acquisition achieves an accuracy of ~ 100 μsec.
The correlator provides a synchronization pulse to the DAS to indicate the start of each STA cycle via an STA interrupt. This information is also supplied to the DAS via one of the bits of the data bus, referred to as the data synchronization bit. The DAS software uses this information to (1) do a consistency check (2) determine the start of the STA data in a stream of continuous data flowing on the data bus from the MAC. The DAS card also receives an interrupt signal at the start of each minute from the GPS receiver. The interrupt handler (the software which does time critical operations when a hardware interrupt is received) for both these interrupts (STA and GPS interrupts) reads the PC time from the PC RTC at each interrupt and maintains a list of corresponding PC time stamps. The list of PC time stamps recorded at each GPS interrupt is then examined for a constant difference of 1 minute. A continuous series is selected such that the time difference between successive samples is accurate to 100 μsec. This series of PC time stamps is referred to as a series of “good” GPS-interrupted time stamps. This series is used to set up a linear equation between the GPS time and the PC time. Since GPS time can be easily converted to the local time standard (Indian Standard Time or IST), this equation essentially converts the PC time to accurate IST time. This equation provides a first order calibration of the PC time, and takes care of any short glitch in the PC time (which can happen due to variety of reasons including overloading of the PC bus). Similarly, the PC time is recorded at each STA interrupt. This list of STA-interrupted PC time stamps is also examined and a continuous series selected such that the time difference between successive PC time stamps is equal to one STA cycle, to an accuracy of 100 μsec. This series of “good” PC time stamps is used to set up a linear relation between the PC time and STA time. The PC time to IST time equation is then used to convert the STA time to IST time, and is also used to tag each STA data block with a sequence number.
The three sources of timing information to the DAS (1) the STA interrupts (2) the GPS interrupts, and (3) the data synchronization bit, all provide time information with respect to the PC RTC. In the above scheme, on a short time scale, unless all these three sources produce drifts and/or glitches, time stamping of the data will remain accurate to 100 μsec. Since all these are independently running clocks, the probability of all three producing error at the same time is very low and it has been shown that the above time stamping scheme is quite robust to short time scale glitches and time drifts.
To account for slow drifts in the PC time, an attempt is made to set up a new linear equation between the STA sequence number and PC time after every 16 STA cycles. The new relation is not accepted unless it matches with the previous one within 100 μsec. Similarly, a new relation is set up between GPS and PC time at each GPS interrupt.
On a longer time scale, an error can occur due to some catastrophic error in either of these sources (e.g. the interrupts not arriving at the PC due to hardware failures). If the DAS software cannot set up the new equations for more than a threshold time interval, it is assumed that an irrecoverable error has occurred rendering the current equations invalid. In such a case, the DAS sets up fresh equations and the data between such an event and the time interval required to set up valid equations is unreliable and is flagged. In practice, however, such events are very infrequent.
However, a slow drift in the PC RTC, with respect to which all three sources of timing information are measured, can produce a drift in the final IST time stamps in the data. Data blocks are expected to arrive at the DAS at a pre-determined constant rate. Data blocks themselves therefore can be effectively used as yet another clock, which is independent of the PC time. Any drift of the PC clock will show up as a consistent shift in the equations between the GPS and PC time and between STA and PC time with respect to the arrival of the data blocks. Hence, any consistent error in the arrival of the data blocks measured with respect to the IST time, derived from the two linear equations, will indicate a drift in the PC time. This fact is used to monitor a slow drift in the PC time over the time scale of setting up new equations.
The PC time is also synchronized to the minute pulse from the GPS. Errors in the PC RTC less than half a minute can therefore be corrected and PC clock synchronized to the GPS clock. However if the PC RTC is in error by more than half a minute, this synchronization will result into minimum of 1 min in the PC RTC. It is therefore important to set the PC RTC to within 1∕2 min of the GPS time.
As mentioned earlier, the compensating delay (equal to τg + τFix; see Section 2.1.1, page 86) which needs to be applied to one of the antennas of an interferometer is applied in the GMRT correlator in two stages. A delay equivalent to an integral multiple of the correlator clock (τInt) is applied in the Delay/DPC section of the correlator. The input data stream is copied into a dual port RAM at the location given by the write-counter. Data is read simultaneously from this RAM from the location given by the read-counter. The offset between the read- and the write-counters for this RAM is maintained such that the read-counter lags behind the write-counter. Since the output samples are read with a time delay (equal to the difference between the counters multiplied by the correlator clock cycle), the output data stream corresponds to the input data stream with a time delay. The time delay, however, can only be in multiples of the correlator clock cycle. The residual delay, corresponding to a fraction of the correlator clock cycle is applied in the fractional sample time correction or FSTC operation. The last stage of the FFT butterfly network provides a facility to apply a channel dependent phase. The frequency channel dependent time varying, phase corresponding to this residual delay, represented by τFSTC, is applied as a linear phase gradient across the band as
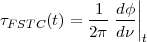 | (2.21) |
Note that τFSTC includes the residual delay due to delay resolution in the Delay/DPC system of the correlator plus the channel dependent residual delay of Equation 2.18.
The output of the FFT stage of the correlator is a set of 256 independent complex numbers. These complex numbers are represented by three 4-bit numbers; one each for the mantissa of real and imaginary parts and one for a common exponent. The complex gains, applicable at the last stage of the FFT butterfly network, are represented by 5 bits each for the real and imaginary parts but has no exponent bit. Thus the channel dependent phase gradient for the FSTC is also limited to a 5-bit representation.
The FFT stage of the correlator performs a real-time Fourier transform of the input signal effectively splitting the input bandwidth of Δν into 128 frequency channels, each of width Δν∕128 (the FFT stage of the correlator can be treated as a set of 128 filter banks). The time series from each of the 128 frequency channels from an antenna, are then multiplied with the corresponding channels from all other antennas, before being integrated in the MAC section of the correlator. The effective input bandwidth, as seen by the multiplier is therefore Δν∕128. For the GMRT, the maximum value of Δν is 16 MHz corresponding to a maximum channel width of 125 KHz, giving a fringe washing function of width ~ 8 μsec. Therefore, for the GMRT correlator, the residual delay must remain less than a fraction of this width (typically less then few micro seconds).
In the final double sideband correlator, in the continuum, non-polar mode, the correlator can be used to record the two co-polar visibilities (the nominal RR and LL correlations) per antenna with a full bandwidth of 32 MHz (both sidebands). In the current single sideband correlator only one sideband of 16 MHz can be processed. In the full polar mode, which will be available with the dual sideband correlator, the cross polar visibilities (namely RL and LR) cal also be recorded. Since the correlator can handle only 256 channels per antenna at the MAC stage, the cross polar mode can be used with only one of the sidebands with a maximum bandwidth of 16 MHz.
The GMRT correlator naturally produces spectral visibilities with a maximum of 256 channels across the entire observing band, if only one polarization is used, or with 128 channels, if both polarizations are used. For normal continuum observations, the 128 channels across a 16 MHz band provide a channel resolution of 125 kHz. For observations where bandwidth smearing is not important (and in the absence of RFI), these channels can be collapsed on-line to produce continuum visibilities. At lower frequencies where primary beams are large, bandwidth smearing can be important for sources away from the phase centre. Also, at frequencies below 610 MHz, intermittent RFI is always a possibility. To reduce bandwidth smearing and to detect and flag narrow band RFI-contaminated data, all the 128 channels are usually recorded. Provision for frequency averaging before recording does however exist and can be used where RFI and bandwidth smearing problems are not perceived to be serious.
For spectral line observations, channel resolution can be increased by controlling the sampling rate of the input signal. The sampling rate can be changed between 32 MHz and 0.125 MHz in steps of two. This corresponds to an effective bandwidth between 16 MHz and 0.25 MHz with a frequency resolution between 125 kHz and ~ 1.95 kHz respectively.
A synthesis radio telescope measures the two-dimensional spatial frequency spectrum of the source structure. Instantaneous projected separations between the elements of the interferometer in the uvw-frame determine the spatial frequency being sampled by the antenna pairs. The projected separation between the antennas, given by w, gives rise to the geometrical delay which needs to be compensated by delay tracking before the signals are multiplied. The value of w is given by
![w = [X cos(H ) - Y sin(H )]cos(δ)+ Z sin(δ)
ij ij ij](thesis141x.png) | (2.22) |
where (Xij,Y ij,Zij)=(Xi -Xj,Y i -Y j,Zi -Zj). The geometrical delay is therefore a function of the relative antenna positions. Precise measurement of the relative locations of the antennas is hence important for phasing the array, which is necessary for imaging with such a telescope.
The radio frequency (RF) signals from the two orthogonal feeds of the antenna are converted to two separate intermediate frequencies (IF) and brought to the Central Electronics building (CEB) for correlation via the optical fiber cables. The fixed delay suffered by the signals from each antenna varies from antenna to antenna since the physical length of the optical fibers to various antennas differ. This fixed delay is largely constant, showing small and slow variations due to changing ground temperature. Since the optical fiber cables are dispersive, any relative fixed delay between antenna pairs results in a time invariant phase ramp across the band in the visibility data. This phase ramp must also be removed or calibrated before averaging the channels to produce the continuum visibilities or before being used for imaging.
The following two sections describe the methodology used and results of baseline and fixed delay calibration.
Historically, the GMRT antenna positions were first determined using theodolite measurements. These were refined using P-band observations following the procedure laid down by Bhatnagar & Rao (1996). Later, dual frequency GPS measurements (Kulkarni 1997) were done to independently determine the antenna co-ordinates.
The GPS measurements provided the antenna co-ordinates relative to the reference GPS antenna, to a quoted accuracy of ~ 2 cm. However, monitoring the phase as a function of hour angle at 327 MHz indicated errors in excess of few meters for some antennas. These GPS co-ordinates were then further refined using P-band observations of celestial sources. Antenna based phases were determined using the GMRT off-line program rantsol (Bhatnagar 1999) from a continuous (~ 7 hours) tracking of 3C48 at 327 MHz. The antenna based phases were modeled as a function of hour angle to measure the relative antenna co-ordinates (see below and Bhatnagar & Rao (1996)). The set of co-ordinates from these measurements were accurate to ~ 1 m for the arm antennas and ~ 0.1 m for the central square antennas. The phase variations at 327 MHz due to other factors (~ 30 arcsec error in antenna pointing which was later corrected, ionospheric contributions, etc.) did not allow determination of X and Y to better accuracies. The Z co-ordinate could not be calibrated at 327 MHz since not enough 327-MHz calibrators could be found which could cover a large declination range but were close enough in hour angle. The proximity of calibrators in hour angle for Z calibrations was necessary to eliminate any unwanted scatter in the phase as a function of declination due to residual errors in the X and Y co-ordinates (see page 135).
These co-ordinates were then further refined using L-band observations (Chengalur & Bhatnagar 2001). Since the residual phase is proportional to the projected baseline length measured in units of the wavelength of the incident radiation, L-band is the best frequency to determine the residual co-ordinate errors in the antenna positions. For this purpose, VLA L-band calibrators 0217+738 and 1125+261 were tracked for several hours at 1280 MHz to compute the antenna based phases. Corrections of 0.5 - 1 m, consistent with the residual co-ordinate errors from the 327-MHz measurements, were found for a few antennas. The final co-ordinates for the Central Square antennas are now known to an accuracy of ≈ 0.05 m. The residual phases for arm antennas correspond to position errors of 0.02 - 0.36 m. These errors do not repeat from day-to-day and are also different for different sources indicating that the residual phases are probably not due to antenna position errors.
|
|
Assuming no errors in the antenna pointing (ΔH = Δδ = 0), the antenna based phase for an antenna with a position error of (ΔX,ΔY,ΔZ) with respect to a reference antenna located at the origin ((X,Y,Z) = (0,0,0)), as a function of the hour angle and declination is given by
![νo
ϕ = 2π-RF-[ΔX cos(δ) cos(H )- ΔY cos(δ)sin (H )+ ΔZ sin(δ)]+ 2πτFixνIF
c](thesis142x.png) | (2.23) |
where νRF o is the frequency of the centre of the RF band, H is the Hour Angle, δ is the declination of the phase center, τFix is the fixed delay suffered by the signal at the IF frequency νIF and c is the speed of light. The orientation of the X, Y, and Z axis is shown in Fig. 2.1.
As can be seen from Equation 2.23, an error in Z will contribute a constant phase for a fixed value of δ. It is therefore necessary to observe a number of sources at different declinations to distinguish between the phase contributed by the terms involving ΔZ and τFix (both of which are independent of H).
The terms involving ΔX and ΔY in Equation 2.23 have a sinusoidal dependence on H. Hence, by tracking a point source for several hours (to get coverage in H while keeping δ constant), the left hand side of the above equation can be modeled as
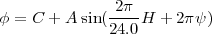 | (2.24) |
where C is a constant and H is in unit of hours. Equating this to the RHS of Equation 2.23 the expressions for ΔX and ΔY (in meters) can be written as
A and ψ can be measured by fitting Equation 2.24 to the antenna based phases, with A, C and ψ as the parameters of the fit. Equations 2.25 and 2.26 then gives the antenna position errors along the X- and Y-axis. ϕ, which is the antenna based phase computed with respect to the reference antenna located at the origin, was computed as a function of Hour Angle using the program rantsol. Equation 2.24 was then fitted to the phases from individual antennas to derive the values of C, A and ψ and Equations 2.25 and 2.26 used to derive the corrections for the X and Y co-ordinates of the antennas.
|
|
The ΔZ correction requires observation of point sources at various declinations. A set of VLA L-Band calibrators with L-band flux densities > 1 Jy and covering a declination range of ≈±40∘ were used to measure ΔZ. Since the observations of each of these calibrators were separated in time, any residual error in the X and Y co-ordinates would reflect in the data as an undesirable spread of the phases as a function of declination. To minimize the effects due to residual errors in X and Y co-ordinates, these calibrators were chosen to be within ~ 1h of each other in Right Ascension. The Z co-ordinate can then be found by fitting ΔZ sin(δ) to the antenna based phase as a function of declination. The final antenna co-ordinates, measured using this procedure, are tabulated in Table 2.3. The list of calibrators used for this purpose is given in Table 2.4. A typical phase variation as a function of declination, before and after correcting for the Z co-ordinate, is shown in Fig. 2.10. The variation of phase as a function of HA derived from ~ 5h long observation of 3C286 (28 Jy at 327 MHz), for a representative set of Central Square and arm antennas is shown in Figs. 2.11 and 2.12 respectively. The source of the short term drifts of ≈ 5 - 10∘ is likely to be the ionosphere. Phase variations over similar time scales and magnitude have been seen at the VLA and have been, to some extent, corrected using GPS based measurements of the variation in the ionospheric total electron content (Erickson et al. 2001).
The estimated accuracy of the antenna co-ordinates, derived from the variations in the phase as a function of hour angle and declination is ~ 5 cm. This will produce a maximum phase variation of ~ 0∘.2 per degree in declination and ~ 5∘ per hour in hour-angle at 1420 MHz due to errors in the antenna co-ordinates. Thus, observations of a calibrator located 20∘ away in the sky from the target source every half-an-hour, would result in a phase error of a few degrees when the antenna based complex gains derived from the calibrator scans are transferred to the data on the target source. These figures will be scaled down by a factor of ~ 4 at 327 MHz. At this level, phases of many antennas drift in an unsystematic manner and constitute the source of dominant phase errors. The residual phase errors due to errors in the antenna co-ordinates after fringe stopping are therefore negligible.
|
|
|
|
|
|
The geometrical delay τg is suffered by radiation at the RF frequency νRF while the dominant fixed delay is suffered at the IF frequency νIF . The compensating delay is applied at the base-band (BB) frequency νBB at the correlator. The total time delay applied at the correlator, (τcorr) is therefore related to τg and τFix as
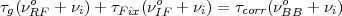 | (2.27) |
where νi is the centre frequency of the ith frequency channel and equal to iν where Δν is the channel width. νRF o,νIF o and νBBo are the centre frequencies of the RF, IF and the base-band respectively. Noting that νBBo = 0 the above equation can be written as
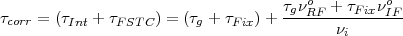 | (2.28) |
τInt corresponds to the time delay applied at the Delay/DPC stage while τFSTC corresponds to the residual delay applied in the FSTC operation (see Section 2.5.2).
In terms of the various frequency conversions in the signal flow, the RF band, for the purposes of delay compensation, can be written in terms of the first and the second local oscillator frequencies (which convert the RF signal to IF signal and the IF signal to baseband signal respectively) as νRF o = νLO1 + νLO2 where, νLO1 and νLO2 are the the first and the second local oscillator frequencies respectively.
|
|
|
|
The residual phase across the band after delay compensation can therefore be written as
Assuming that τInt + τFSTC accurately compensates for τg, τFix can be written as
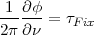 | (2.30) |
The largest contribution to the fixed delay is due to the propagation delay in the optical fibers from the antenna base to the Central Electronics Building (CEB). These delays were measured by computing the antenna based complex gains for each of the 128 channels using the off-line program rantsol, for a strong point source observed at 327 MHz using the full band 16 MHz. This essentially provided the antenna based amplitude and phase across the band. The slope of the phase across the band was measured and τFix derived using the Equation 2.30 (the slope of phase as a function of frequency). The fixed instrumental delays thus measured are also listed in Table 2.3. The phase across the band before and after the fixed delay correction is shown in Figs. 2.13 and 2.14 respectively for a representative set of antennas.
For interferometric observations, frequency averaging (to produce continuum or multi-channel continuum visibilities) is done after correlation and only the relative fixed delays are important. Since the same set of reasonably identical filters are selected at all antennas, the relative change in the fixed delays due to change of filters is not large. Also, since the ground temperature variation is similar from antenna to antenna and slowly varying over the scale of the array, its contribution to change in delays is not large. Although the delay component due to the filter selection and that due to diurnal variations must ultimately be tabulated and used for the delay compensation software, it is not a limiting factor and can be easily calibrated. The phase calibrators used for the continuum mapping observations used in this dissertation were strong (> 5 Jy) and were observed every half-an-hour. The antenna band shapes were computed from the data on these calibrator scans and the interpolated gains for each channel applied to the visibilities of the target source. This provided the calibration for changes in the delay due to filters (small and fixed as function of time) and diurnal variations (small and slowly varying in time).