Value of x = 1.00000 +/- 0.10000 Value of y = 2.00000 +/- 0.20000 Value of x1 = 1.00000 +/- 0.10000 Value of x2 = 1.00000 +/- 0.10000 sin(x) = 0.84147 +/- 0.05403 sqrt(1-sin(x)^2) = 0.54030 +/- 0.08415 cos(x) = 0.54030 +/- 0.08415 tan(x) = 1.55741 +/- 0.34255 sin(x)/cos(x) = 1.55741 +/- 0.34255 asin(sin(x)) = 1.00000 +/- 0.10000 asinh(sinh(x)) = 1.00000 +/- 0.10000 atanh(tanh(x)) = 1.00000 +/- 0.10000 exp(ln(x)) = 1.00000 +/- 0.10000 sinh(x) = 1.17520 +/- 0.15431 (exp(x)-exp(-x))/2 = 1.17520 +/- 0.15431 sinh(x)/((exp(x)-exp(-x))/2) = 1.00000 x/exp(ln(x)) = 1.00000 sin(x1)*sin(x1) = 0.70807 +/- 0.09093 sin(x1)*sin(x2) = 0.70807 +/- 0.06430 sin(x1)^2+cos(x1)^2 = 1.00000 +/- 0.00000 sin(x1)^2+cos(x2)^2 = 1.00000 +/- 0.12859
Following is an example of error propagation in a recursive function.
The factorial of ![]() is written as a recursive function
is written as a recursive function ![]() . Its
derivative is given by
. Its
derivative is given by
![]() . The term in the parenthesis is also written
as a recursive function
. The term in the parenthesis is also written
as a recursive function ![]() . It is shown that the propagated
error in
. It is shown that the propagated
error in ![]() is equal to
is equal to
![]() .
.
>f(x) {if (x==1) return x; else return x*f(--x);}
>df(x){if (x==1) return x; else return 1/x+df(--x);}
>f(x=10pm1)
3628800.00000 +/- 10628640.00000
>(f(x)*df(x)*x.rms).val
10628640.00000
Similarly, the recurrence relations for the Laguerre polynomial of
order 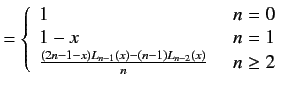 |
(5) | ||
| (6) |
>l(n,x){
if (n<=0) return 1;
if (n==1) return 1-x;
return ((2*n-1-x)*l(n-1,x)-(n-1)*l(n-2,x))/n;
}
>dl(n,x){return (n/x)*(l(n,x)-l(n-1,x));}
>l(4,x=3pm1)
1.37500 +/- 0.50000
>(dl(4,x)*x.rms).val
0.50000