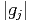 2w
ij. Since the
denominator is the sum of this effective weight, the right-hand side of Eq. 8 can
be interpreted as the weighted average of gi over all correlations with antenna
i.
2w
ij. Since the
denominator is the sum of this effective weight, the right-hand side of Eq. 8 can
be interpreted as the weighted average of gi over all correlations with antenna
i.
Eq. 8 offers itself for some intuitive understanding in the following way.
Xij is a product of two complex numbers, namely gi and gj⋆, which we wish to
determine. Xij is itself derived from the measured quantity V ijObs. Numerically speaking,
each term in the summation of the numerator of Eq. 8 will involve gi (via Xij) and the
multiplication of Xij with gjwij would give gi an effective weight of 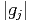 2w
ij. Since the
denominator is the sum of this effective weight, the right-hand side of Eq. 8 can
be interpreted as the weighted average of gi over all correlations with antenna
i.
2w
ij. Since the
denominator is the sum of this effective weight, the right-hand side of Eq. 8 can
be interpreted as the weighted average of gi over all correlations with antenna
i.
In the very first iteration, when gj = (1, 0), the normalization would be incorrect since the numeric value of gj as it appears inside Xij would be different from that used in the denominator of Eq. 8. However, as the estimates of gjs improve with iterations, the equation would progressively approach a true weighted average equation. The speed of convergence will depend upon the value of α and the convergence would be defined by the constraint in Eq. 10. In the ideal case when the true value of all gis is known, right hand side of Eq. 8 also reduces to gi.
Estimating gi for an antenna, by averaging over the measurements from all baselines
in which it participates (for an unresolved source) makes sense since for an N element
array, gi would be present in N-1 measurements (all the Xij|j=1,N;j≠i) and the best
estimate of gi would be the weighted average of all these measurements. Proper weight for
gi, buried in each of the products Xij, can be found heuristically as follows. gi,
estimated from the measurements of a given baseline, must obviously be weighted by
the signal-to-noise ratio on that baseline. This is wij in the above equations. It
must also be weighted by the amplitude gain of the other antenna making the
baseline, namely gj, to account for variation in antenna sensitivities and Tsys. The
total weight for gi would then be 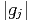 2w
ij, the sum of which appears in the
denominator of Eq. 8. Knowing that ideally Xij = gigj⋆, each of the X
ij|j=1,N
must be multiplied by gjwij (to apply the the above mentioned weights to gi),
before being summed for all values of j and normalized by the sum of weights to
form the weighted average of gi. One thus arrives at Eq. 8 using these heuristic
arguments.
2w
ij, the sum of which appears in the
denominator of Eq. 8. Knowing that ideally Xij = gigj⋆, each of the X
ij|j=1,N
must be multiplied by gjwij (to apply the the above mentioned weights to gi),
before being summed for all values of j and normalized by the sum of weights to
form the weighted average of gi. One thus arrives at Eq. 8 using these heuristic
arguments.