Consider using the actualDurations table
to store one weight per polarization product per spectral
window per baseband per baseline. Assume, further, that the
number of phase bins and APC bins is fixed to be one in all
spectral windows. Note that the number of spectral channels
may vary with spectral window, but there is only one
weight per polarization product that applies to all spectral
channels within each spectral window. The key
phrase in the foregoing sentence, which is emphasized, is a
sign that the spectral channels axis may be omitted from the
table in the data stream. The following XML snippet would be
part of the sdmHeaderData element that
describes this table.
Example A.1. Omitted axes table header snippet
This example needs some updating.
<actualDurations size="18144"ref="actualDurations" axes="a1 a3 a4 a5 a6 a7"
/> <numAntenna>27</numAntenna> <numAPC>1</numAPC> <baseband> <spectralWindow numBin="1" numSpectralPoint="512" numPolProduct="2"/> <spectralWindow numBin="1" numSpectralPoint="1024" numPolProduct="4"/> </baseband>
<correlatedData type="float" size="15482880"
ref="crossData"/>
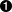 | 8 ⋅ 378 ⋅ (4 + 2) [using Equation A.1, “Binary table size” and the section called “actualDurations table”] |
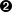 | “a2”, the spectral channel axis, is missing. |
 | The number of spectral channels and polarization products vary among spectral windows within the baseband. |
 | 2 ⋅ 4 ⋅ 378 ⋅ (512 ⋅ 2 + 1024 ⋅ 4) [using Equation A.1, “Binary table size” and the section called “crossData table”] |
The actualDurations table will be indexed as Abl,bb,sw,pb,ab,sc,pp . However, for optimization, the table in the data stream has omitted the sc axis since the data have no dependency on spectral channel; that is, the data in the table are indexed as Tbl,bb,sw,pb,ab,pp . The mapping of an index for A to the equivalent index for T is simply (bl, bb, sw, pb, ab, sc, pp) ↦ (bl, bb, sw, pb, ab, pp) . For example, the following statements hold.
| A15,0,0,0,0,100,1 = A15,0,0,0,0,200,1 |
| A15,0,0,0,0,100,1 = T15,0,0,0,0,1 |
| A15,0,0,0,0,200,1 = T15,0,0,0,0,1 |
| A15,0,0,0,0,42,1 ≠ A15,0,1,0,0,42,1 ⇔ T15,0,0,0,0,1 ≠ T15,0,1,0,0,1 |