Lecture 8 - The Solar System: An Overview (10/6/98)

Energy --- | --- Radiation

Reading:

Chapter 2, 3-3 (ZG4)

	Key Question:	How do we know that the heliocentric model is "correct"?
	Key Principle:	Angular Momentum Vector
	Key Problem:	Why are all the planetary orbits approximately in the same plane?
	Key Quote:	"At what point would you accept the heliocentric model over the geocentric model?"

Investigations:

1. Orbital Motion Effects
   • How does stellar aberration demonstrate that the Earth revolves around the Sun?
   • What is stellar parallax?
   • Which components of the Earth's velocity are relevant for aberration and parallax?
   • What is a parsec?
   • How do we use parallax to determine distances?
   • What is the angle subtended by the Earth's orbit at a distance of 1 parsec?
2. The Doppler Shift
   • What is an electromagnetic wave?
   • What is the frequency of a 1-meter radio wave?
   • What is the frequency of a 1-cm microwave?
   • What is a typical wavelength for visible light?
   • Does a moving observer measure a different wavelength for light emitted from a stationary source?
   • For relative motion along the line-of-sight, what is the change in wavelength?
   • For relative motion transverse to the line-of-sight, what is the change in wavelength?
   • What is the small velocity limit of the Doppler shift?
   • How can we use the redshift or blueshift of spectral lines to measure relative velocities?
   • What is the wavelength shift (in Angstroms) for visible light corresponding to the Earth's orbital velocity?
   • How can we use Doppler shifts to detect unseen companion planets to distant stars?
3. Are we moving?
   • What are the series of steps we took to move from the geocentric to the heliocentric models?
   • At what point would you have accepted the heliocentric model?
   • In what sense are different frames of reference (geocentric, heliocentric, galactocentric, etc) equivalent?
   • How is this sort of debate, and changing of paradigm, fundamental to cosmology?
4. Inventory of the Solar System
   • What are the terrestrial planets?
   • What are the Jovian planets?
   • What sort of planet is Pluto? Its moon Charon?
   • Which planets were known to the ancients and which were discovered in the 18th, 19th, and 20th centuries?
   • What are asteroids and where is the main asteroid belt?
   • What are comets and meteors?
   • What are the satellites of the planets made of?
   • Which planets have rings?
   • What is the zodiacal light due to?
   • What is the solar wind?
5. Constituent Matter in the Solar System
   • What are the four states of matter?
   • What are the three kinds of solids?
   • What are the two fluids?
   • What type of bodies are mainly rock, and metal? Ice? Gas?
   • What sort of liquids are there?
   • Where is plasma found?
   • What sort of radiation is found in our solar system?
6. Solar System Mechanics
   • Why are all planetary orbits prograde?
   • Which planet shows retrograde rotation?
   • Which planet has a rotation axis tilted 90 degress to its orbit?
   • Which planet has the highest inclination to the ecliptic, and most eccentric orbit? Why?
   • What spin-orbit resonances are found in the solar system?
   • What orbital resonances are found between planets? Why?
   • Will Pluto run into Neptune in the near future? Why might it have survived on a Neptune crossing orbit?

Motion of the Earth:

Check out the webpage from Scott Anderson of Emory University illustrating nicely the motion of the Earth. The animations are fairly effective.

Stellar Parallax:

The small angle formula tells us that the angle (in radians) subtended by an object of diameter D at distance r is:

= D / r

This can be turned around in that if we observe an object shift direction by this angle (in radians) when we move a distance D perpendicular to its direction, then it must be at a distance r.

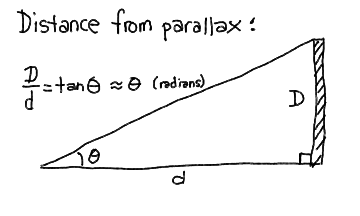
There are 206265 arcseconds (") in a radian, so the angular size of an object of diameter D at distance r is

" = 206265 * D / r

If we use the baseline of the Earth's orbit (2 AU for 6 months apart) and see a shift of theta = 2 * p arcseconds, then

It is customary to define p as the parallax. Thus a parallax p of 1" means that the distance r is 206265 AU. If we define the unit of distance called the parsec to be 1 pc = 206265 AU, then

A star 1 parsec away has a parallax of 1 arcsecond. Talk about convenience! Note that 1 pc is about 3.26 light-years. The nearest star is around 1 pc away.

Steps Toward the Heliocentric Model:

Aristarchus	measured distance to Sun (incorrectly!) and discovered it to be much larger than the Earth
Copernicus	introduced heliocentric model which easily reproduced retrograde motion, but was inaccurate compared to Ptolemaic model
Kepler	Laws of Motion with elliptical orbits produce highly accurate heliocentric model, without epicycles
Galileo	observes phases of Venus and moons of Jupiter, and uses these to argue vociferously for heliocentric model over geocentric
Newton	Laws of Motion and Universal Gravitation explain Kepler's Laws, including comets, and provide physical basis for gravitation
19th Century	binary stars discovered; stellar parallax and aberration measured
Einstein	General Theory of Gravitation extends Newtonian gravity; framework for cosmology and expanding universe models
Late 20th Century	Extrasolar planets found through pulsar timing and Doppler measurements of stellar radial velocities

I didn't get to it in this lecture, but there have been a number of numerological attempts to explain the spacings of the planetary orbits in our solar system.

One such scheme, proposed in 1766 by Johann Titius and popularized later by Johan Elbert Bode, uses a series to approximate the orbital spacings of the planets. It has no solid physical basis, and can be thought of as a "fitting function". It was surprising that this rule, developed before the discovery of Uranus, Neptune, and Pluto, as well as the main belt asteroids such as Ceres, holds for nearly all the planets.

The rule can be written generally as:

for the semi-major axis a_n of the n-th orbit, where n takes on the values

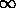n = -, 0, 1, 2, ...

The constants p, b, q are determined by the first three orbits

1	n = -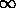	a = p	0.4 AU	Mercury
2	n = 0	a = p + b	0.7 AU	Venus
3	n = 1	a = p + b q	1 AU	Earth

thus p = 0.4, b=0.3, q=2. Check this for yourself!

This rule can also be written in recursive notation

where in our case q=2 and c=0.4.

The upshot for our solar system is that the following orbits are predicted:

Orbit	n	an (AU)	Planet	a (AU)
1	-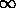	0.4	Mercury	0.39
2	0	0.7	Venus	0.72
3	1	1.0	Earth	1.00
4	2	1.6	Mars	1.52
5	3	2.8	Ceres	2.77
6	4	5.2	Juptier	5.20
7	5	10.0	Saturn	9.54
8	6	19.6	Uranus	19.19
9	7	38.8	Neptune	30.06
10	8	77.2	Pluto?	39.53

Note that the largest main belt asteroid Ceres fits the n=3 orbit. Also, the n=7 orbit seems to be best fit by an average of Neptune and Pluto. Perhaps "Planet X" could lurk out at 77 AU, and Pluto is just an interloper.

Last year, I noticed a paper on fitting random stable solar systems (from simulations) to a Titius-Bode law. If you are interested, you can find this on the LANL Astro-PH Preprint Archive.

Prev Lecture --- Next Lecture --- Astr11 Index --- Astr11 Home

smyers@nrao.edu Steven T. Myers