Flux Standards Restructuring
Last modified: 2013-07-26
For CASA 4.2 development, in order to fully support Perley-Butler 2013 standard
including the time-variable sources, restructuring in the flux standard
related code in casacore (under ~/comoponents/ComponentModels/) was performed.
Main changes are:
FluxStdsQS.{h,cc} were replaced by FluxStdQS2.{h,cc} (may be renamed to FluxStdsQS.{h,cc} later).
FluxCalcQS.{h,cc} were replaced by FluxCalcVQS.{h,cc}
Refactored the source name and position data from FluxCalcQS.cc to encapsulate FluxStdSrcs class
For the new standards, Perley-Butler 2013 and Scaife-Heald 2012, the coefficients for a polynomial describing spectral models are stored in the separate data tables and not in FluxStdsQS2.cc.
For time-variable sources in Perley-Butler 2013, fluxes are computed at each epoch and interpolated
with a user specified interpolation method with the default being 'nearest'(-neighbor).
Perley-Butler 2013
The spectral flux density models from Perley and Butler 2013, ApJS 204, 19.
This includes the support for time-variable sources listed in Perley & Butler 2013.
The coefficient data : PerleyButler2013Coeffs
Stored in a Casa table in the data directory, under ~/data/nrao/VLA/standards/.
Each row contains the coefficients and their errors
of all the standard sources at a certain epoch. For the sources considered to be non-variable
these coefficient values are identical for all the rows.
The polynomial function assumed here is,
log(S(νGHz)) = a0 + a1*log(νGHz)+a2*(log(νGHz))2 + a3*(log(νGHz))3,
where S is the flux density in Jy and νGHz is the frequency in GHz.
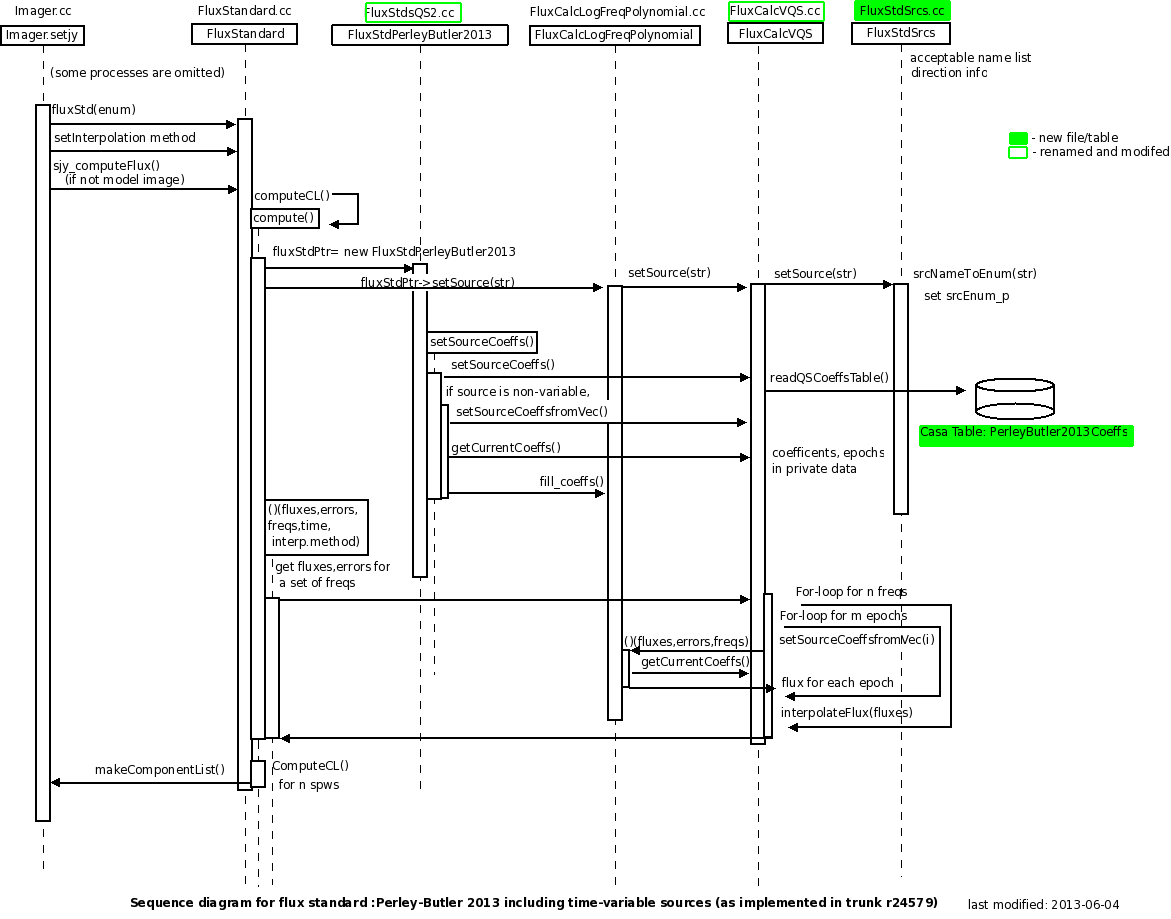
The current sequence diagram of the Perley-Butler 2013 standard as shown below.
Scaife-Heald 2012
The broad-band flux scale based on Scaife and Heald 2012, A&A, 423L at low frequencies(below 500HMz).
As in Perley-Butler 2013, the coefficients are read from a CASA table.
Originally implemented by Huib Intema in the older CASA code and it has been merged to the current trunk.
The coefficient data : ScaifeHeald2012Coeffs
The table consists of a single row containing the coefficients and their errors.
The polynomial function assumed here is,
log(S(ν)) = log(a0) + a1*log(ν/νref) + a2*log(ν/νref)2 + a3*log(ν/νref)3 + ...,
where νref is the reference frequency, =150MHz.
T.Tsutsumi
