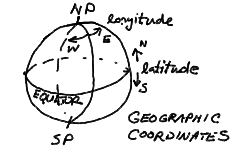
We wish to set up the coordinate systems that we use to map the positions of stars, planets, and other astronomical objects on the sky. We will start with the geographic coordinate system of the Earth globe. We are used to thinking about the Earth as a sphere, with a rotation axis that passes through the surface at the North and South geographic poles. The circle of the equator marks the plane perpendicular to the Earth's axis and divides the Earth into the northern and southern hemispheres. The postion of any point on the globe is given by the latitude, measured in the plane containing the point and the Earth's axis, in degrees running from +90 to -90 (north to south), and the longitude measured from the prime meridian (Greenwich meridian) on the constant latitude circle containing the point and parallel to the equator, in degrees 0 to 180 East or West of the prime meridian.

The celestial coordinate system for defining the positions of stars and such are just extensions of the geographic coordinate system. One could think of stopping the rotation of the Earth in some convenient place in its orbit, then projecting the position of any star down onto the globe's surface on the radial line outward from the Earth's center. This is what is meant by the celestial sphere, and it is usually pictured as a larger sphere containing the Earth and concentric with the Earth - every point on the Earth has a point directly above it on the celestial sphere, and every star on the celestial sphere has a point on the Earth directly below. On the celestial sphere, the North Celestial Pole (NCP) and South Celestial Pole (SCP) correspond directly to their geographic counterparts, as does the Celestial Equator. The coordinate system is also a direct analog, with declination (Dec) measured as the latitude is on the globe, and the right ascension (RA) corresponding to longitude - though for right ascension, the angle is measured in units of 0 to 24 hours from the zero-hour point. This is because rotation causes the place of the celestial coordinates above the Earthbound observer, so the right ascension of an object gives the number of hours since the zero-hour circle was at the same position in the sky.
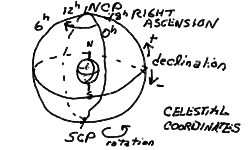
To define the celestial coordinate system, it only remains to fix the zero meridian of right ascension. We will define the position of the Sun at the vernal equinox to be at 0 RA (and at 0 Dec). The geographic coordinates then line up with the celestial coordinates at noon on the vernal equinox on the Greenwich meridian of the Earth. We will discuss this further when we come to the cycles of the Sun in the sky.
Because the celestial sphere is an extension of the geographic globe, we can also see that the stars with declinations equal to our latitude pass directly overhead. This is true for any observer. Someone on the equator sees the celestial equator overhead, and the NCP and SCP on the north and south horizon respectively. An unlucky astronomer stationed at the north pole sees the NCP overhead, and the celestial equator on the horizon. From this picture, it is easy to see that the angle that we see the NCP above the north horizon (since we live in the northern hemisphere) is just equal to our latitude. Philadelphia is at a latitude of nearly 40 degrees N, so the NCP is 40 degrees elevation above the north horizon.
Because the NCP is marked by a relatively bright star located less than a degree away - named Polaris, remarkably enough - it is easy to spot. Note that there is no such convenient "pole-star" at the SCP! Early navigators on the high seas could find their latitude by simply measuring the elevation angle of Polaris above the horizon using a sextant. Finding longitude, however, required an accurate reckoning of time, since the longitude is given by the time of transit of a given star on the observer's meridian (the north-south line overhead). Much of the boom in world naval exploration was due to the development of chronometers for navigation.
I would like to demonstrate that even if the Earth were locked facing the Sun so that it was always the same solar time, that the celsestial sphere, and thus the distant stars, would be seen to rotate once during the year. Shown below is a rough diagram illustrating two differently colored hemispheres of the Earth locked facing the Sun. Note that the dark colored half rotates once relative to our point-of-view of the stars.
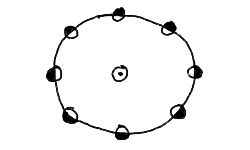
Thus, even if there is no solar day, there is one sidereal day. We now draw the same figure, but with the dark half making two turns with respect to the stars (us looking down on it).
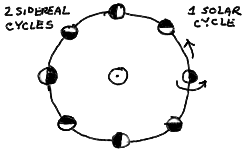
We now see that our "Earth" makes one complete rotation with respect to the Sun, as the white half faces the Sun at the right, and the dark at the leftmost part of the orbit. The year now is one solar day long, but two sidereal days long! It is easy now to see how this will generalize to more days. Q: Try drawing the same picture for 3 sidereal days in the year (Hint: divide the orbit up into 12 earths on the orbit instead of 8). There will always be one more sidereal rotation than solar rotation. If there are 365 solar days in the solar year, then there will be 366 sidereal days in the solar year. Thus, the solar day must be (366/365) x sidereal day!
I will now make a third set of drawings to show the relationship between the sidereal and solar day. I will zoom in on a (greatly exaggerated) step of one day in the orbit of the Earth. We see on the left panel, after one sidereal day, the earth is in the same orientation to us (the stars) as it was at the beginning. The little arrow meant to represent an observer looking upward is pointing in the same direction. But note that at the end of the day it is no longer pointing at the Sun! This is because our orbit has carried us around a little ways, and the Sun now appears in a different direction (a little eastward). To bring our arrow to point at the Sun again, we have to move a fraction of a rotation farther. From geometry, we know that the angle between the first earth, the Sun, and the second earth, which is just 1/365 of a circle (the orbit), must be equal to the angle between the Sun, the second earth, and the direction to the distant star the second arrow is pointing to. This is 1/365 of a circle then, or 1/365 of a sidereal day (a circle of the earth). Thus we get the panel on the right:
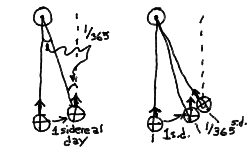
This also shows the importance of drawing pictures to help you understand the geometrical aspects of astronomy. This will become very useful also for understanding the phases of the moon and eclipses.
The coordinate system that we are most used to is that centered about us as we stand looking at the sky. This reference frame is known as azimuth-Elevation (or azimuth-altitude), after the coordinate axes themselves. Altitude or elevation measures the angle above the horizon that an object appears at, while azimuth (AZ) gives the compass angle toward the object. Think of sighting a telescope by swinging it around to the correct compass heading toward the star, then moving upward to bring the star into the viewfinder. Elevation (also sometimes called "altitude") is measured from the horizon, 0 degrees, to the point on the sky directly overhead at 90 degrees - this is called the zenith. Although it isn't visible through the Earth, the point directly opposite the zenith, straight below us, is the nadir. The azimuth is measured North through East along the horizon, with North 0 degrees, East 90 degrees, South 180 degrees, and West 270 degrees. The observers meridian is the circle passing through the zenith from due north to due south (AZ 0 to 180 degrees).
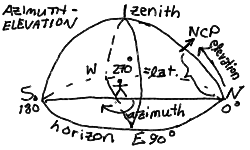
Using these coordinates, the North Celestial Pole (NCP), as discussed in the previous lecture, is at an azimuth of 0 degrees (due north), and an elevation equal to the observer's latitude. In our case, in Philadelphia, this is AZ=0, EL=40. Q: What is the azimuth and elevation of the SCP for an observer in Melbourne, Australia (latitude 38 degrees South)?
It is often more convenient to use the angle down from the zenith, or zenith angle (ZA), than the angle up from the horizon. We will use azimuth and zenith angle to designate the observer-centered coordinates for objects in the sky. Thus, the NCP is at AZ=0, ZA=90-LAT=50 for observers in Philadelphia. The horizon is at ZA=90, in particular, the north horizon is at AZ=0, ZA=90, and the south horizon at AZ=180, ZA=90. The zenith is naturally at ZA=0, and the nadir is at ZA=180, with indeterminate azimuth.
Triginometry on the sky is somewhat different than plane triginometry. Three points on the sky represent three directions. They can also be thought of as three points on a sphere, connected by great circles --- thus, a spherical triangle. The triginometric relations for a spherical triangle are given below.

These relations can be used to solve for the local coordinates of a star, if you use the North Celestial Pole, the zenith, and the star as the three vertices of the triangle.
Part of the battle of understanding the relations between the celestial coordinate systems is visualizing the spherical triangles that relate the various systems. For example, given the right ascension (RA), declination (Dec), and local sidereal time (LST), one can compute the azimuth (AZ) and zenith angle (ZA) of any object in the sky. First, note that the hour angle (HA) is just given by
Furthermore, by placing the north celestial pole (NCP), the local zenith, and the object as vertices of a spherical triangle, the spherical triginometric relations (sine rule and cosine rule) can be used to solve for ZA and AZ. Study the triangle below carefully, and see how using the cosine rule the zenith angle ZA of the object can be computed. (Remember that the zenith angle is the angular distance from the zenith, which is 90 degrees minus the altitude above the horizon). Because the zenith angle is a polar angle, and runs from 0 to 180 degrees (the nadir), with the horizon at 90 degrees ZA, you only need the cosine rule (Q: Why is this true?).

Note that we have used the fact that sin(90-x)=cos(x) and cos(90-x)=sin(x) for angles x in degrees. After solving for the ZA, the triangle can then be solved for the azimuth. This is more complicated, since it goes all the way around 0 to 360 degrees --- both sine and cosine are needed to fully determine the azimuthal angle (Q: Why is this true?). Therfore, both the sine and cosine rules are used. Be sure to get the relative sign of the azimuth versus the hour angle correct by noting that it is measured north through east.

Thus, you can convert RA,DEC to AZ,ZA and the reverse also!
Some of you asked in class how you actually go about using the various coordinate systems to find the positions of objects in the sky. This is just such an example, and it uses Spherical Triginometry (triangles on a sphere) to work a problem.
Note that here "ZA" refers to zenith angle which is the complement of the altitude above the horizon (its the angle down from the zenith, naturally).
The various coordinate systems used in astronomy are confusing until you get used to them. Thus, the first two problems of the homework involve a simple computation of the position of the Sun, which for the purposes of the problem is assumed to be at the fixed RA=12h and DEC=0 degrees. In fact, the Sun moves Eastward against the stars along the ecliptic at about 1 degree per day, so it hardly moves in 2 hours anyway!
First, we review the orientation of the AZ,ZA and HA,DEC systems. Below is a diagram showing the relevant spherical triangle for a star that is about to cross the meridian north of the zenith. From the diagram, it appears its azimuth is near 75 degrees (ENE) and zenith angle is around 30 degrees, and is at an hour angle of about -3 hours.

Suppose we were asked to compute the AZ and ZA of a star that was at DEC=+55 degrees and RA=8 hours at the Local Sidereal Time (LST) in Philadelpha (LAT=+40) of 5 hours. Thus
HA = LST - RA = 5 hours - 8 hours = -3 hours
In our triangle with the vertices the NCP, zenith, and the star, the HA is an interior angle as is the AZ, so we should use -HA. When we use the hour angle, we should convert the hours to degrees (1 hour = 15 degrees), so HA=-45. We then compute the ZA from the cosine rule:
cos(ZA) = cos(90-DEC)cos(90-LAT) + sin(90-DEC)sin(90-LAT)cos(HA)
= sin(DEC)sin(LAT) + cos(DEC)cos(LAT)cos(-HA)
Plugging in HA=-45, DEC=+55, LAT=+40, we get cos(ZA)=0.8372, so the zenith angle ZA=33.15 degrees. We can then use the sine rule to find the azimuth:
sin(AZ) = sin(-HA)sin(90-DEC)/sin(ZA)
= sin(-HA)cos(DEC)/sin(ZA)
Plugging in HA=-45, DEC=+55, ZA=33.15, we find sin(AZ)=0.7417, or AZ=47.88 degrees. We could also have used the cosine rule to find the azimuth:
cos(90-DEC) = cos(ZA)cos(90-LAT) + sin(ZA)sin(90-LAT)cos(AZ)
sin(DEC) = cos(ZA)sin(LAT) + sin(ZA)sin(LAT)cos(AZ)
thus
cos(AZ) = ( sin(DEC) - cos(ZA)sin(LAT) )/( sin(ZA)cos(LAT) )
Which gives cos(AZ)=0.6708, or AZ=47.88 degrees in agreement with the sine rule.
As an example, we might wish to calculate how long the Sun is above the horizon from Philadelphia in midsummer. This translates to finding the hour angle of the Sun at sunrise, as it will be up for twice that. At midsummer solstice (June 21), the Sun is as far north as it gets, at DEC=+23.5 degrees. This is above the Tropic of Cancer for those of you geographically inclined. This is three months after the vernal equinox, so the Sun is at RA=6 hours.

We construct our triangle between the zenith, the NCP, and the Sun on the Eastern horizon. Note that since it is on the horizon, the ZA=90 degrees. The cosine rule gives:
cos(ZA) = sin(DEC)sin(LAT) + cos(DEC)cos(LAT)cos(-HA)
Plugging in ZA=90 for the horizon, we get, noting cos(-HA)=cos(HA),
cos(HA) = -sin(DEC)sin(LAT)/cos(DEC)cos(LAT)
= -tan(DEC)tan(LAT)
For DEC=+23.5, LAT=+40, we get cos(HA)=-0.3649, or HA=111.40 degrees which is 7.43 hours. Thus, the Sun is up for 14.85 hours at midsummer! If we plug in the DEC of the Sun at midwinter, DEC=-23.5, we find cos(HA)=0.3649, so HA=68.60 degrees, or 4.57 hours. Thus, on the shortest day, the Sun is up for only 9.15 hours!
This expression can be useful for finding out whether any object is visible in the sky. For example, for DEC=0, cos(HA)=0 by our formula, so any object on the equator will be up for HA = -6 hours to +6 hours, or LSTs from RA-6h to RA+6h. Thus, when the Sun is on the equator it is call an "equinox", since night and day are equal in length --- 12 hours.
Finally, returning to our midsummer dawn, we might wish to know at what azimuth the Sun will rise. That way, we can properly align our Stonehenge for the pagan festival. This is easy enough to compute:
sin(AZ) = sin(-HA)cos(DEC)/sin(ZA)
which for ZA=90, HA=-111.4, DEC=+23.5 gives AZ=58.63. Align those stones!
As the planets revolve about the Sun in their various orbits, they appear in the sky in different configurations with respect to the Sun. For example, two of the planets, Mercury and Venus, always are found near the Sun --- no more than 47 degrees, in the case of Venus, and no more than about 20 degrees in the case of Mercury. The other naked-eye planets known to early astronomers, Mars, Jupiter and Saturn, can be found anywhere along the ecliptic with respect to the Sun.
The planets with orbits inside of the Earth's orbit, Mercury and Venus, are called inferior planets. The planets with orbits outside the Earth's orbit, Mars, Jupiter, Saturn (and the rest) are called superior planets.
Planets on the opposite side of the ecliptic from the Sun are in opposition, those on the same side are in conjunction. The inferior planets can never be found at opposition, but can be in conjunction on the near side of the Sun (inferior conjunction) or the far side of the Sun (superior conjunction) from the Earth. The superior planets are in conjunction on the far side of the Sun, naturally, and are at closest approach to the Earth during opposition. For superior planets, there are two configurations where the planets is 90 degrees from the Sun. These are known as quadrature.
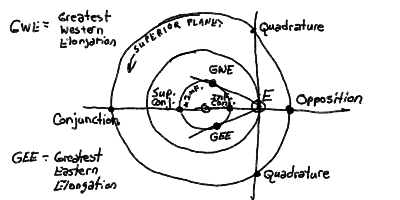
The elongation of a planet is the angular distance from the Sun of the planet. Elongations range from 0 degrees (conjunction) to 180 degrees (opposition) for superior planets. For inferior planets, the elongations reach a maximum --- the greatest eastern elongation and the greatest western elongation --- from the Sun.
It is readily apparent that the Sun changes its RA and DEC throughout the year. It is high in the sky during the summer, and low in the sky during the winter. The night sky constellations change from Orion in the winter to Cygnus and the summer triangle in the summer. While the Earth revolves about the Sun, we see the Sun projected against a different backdrop of stars, or at least we would if we could see the stars in the daytime. The path of the Sun as it treks across the sky during the Earth's orbit is called the ecliptic (for reasons that will become clear in the next lectures). The ecliptic can also be thought of as the intersection of the plane of Earth's orbit with the celestial sphere. The ecliptic is not the same as the celestial equator because the Earth's rotation axis is tipped (see next section).
The rotation of the Earth is most easily defined against the repeating backdrop of stars. This, in many ways, gives us our preferred frame of reference. In one sidereal day, the Earth's rotation carries us around to see exactly the same stars at the same positions in the sky. The sidereal day is approximately 23h 56m 4s. Wait a minute (actually 4 minutes)! Why is this less than our 24 hour day? The day we are used to, the solar day is defined as the time it takes the Sun to be rotated around to appear on the meridian again - from noon to noon. This is longer than the sidereal day because in that day, the Earth has moved through approximately 1/365 of its orbit (the solar year is around 365.26 solar days long), placing the Sun an extra degree or so eastward on the ecliptic. To catch up to the Sun, we have to go just over an extra 1/365.26 of a day, or 4m. (If you were to lock the Earth facing the Sun and watch it revolve in its orbit from above, you would see it rotate one full revolution, or day, with respect to the fixed stars. It is this extra "day" that we need to make up during the year, 1/365 of it each actual day.)
We can define ecliptic coordinates like we have done for celestial coordinates and azimuth-elevation coordinates before. Perpendicular to the ecliptic plane are the North Ecliptic Pole (NEP) and the South Ecliptic Pole (SEP).
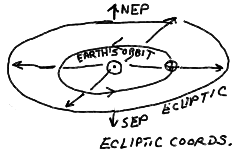
There are 12 constellations through which the ecliptic passes. These are the familiar "signs" of the Zodiac. Early astrology assigned special significance to those constellations through which the Sun, Moon, and planets pass on their celestial wanderings.
In temperate climates such as ours, we notice the cycle of the seasons quite readily. The warm summer is dictated by the Sun high in the sky during the long dog days, while the cold winter is feebly lit by the Sun low in the southern sky in those short days. This is a reflection of the fact that the ecliptic is inclined to the celestial equator by 23.5 degrees, which is equivalent to saying that the Earth's rotation axis is misaligned by 23.5 degrees with the "axis" of Earth's orbit around the Sun. If they were aligned, the Sun would move along the celestial equator and there would be no seasons (at least such as we know them).
It is the intersections of the ecliptic and the celestial equator that we use to define the reference points of our celestial coordinate system. On a sphere, two distinct great circles intersect at exactly two opposite points. In the spring, around the day of March 21, the Sun passes through the celestial equator on its way northward along the ecliptic. This time is known as the vernal equinox, when night and day have equal length, and is generally considered to mark the first day of spring (though it is seldom "springlike" so early!). This point of intersection on the celestial equator marks zero Right Ascension. On this day, the coordinates of the Sun are 0 hours RA and 0 degrees Dec. In the fall, the Sun crosses the equator going southward. This is the autumnal equinox, again with equal night and day. The sun on this day is at 12 hours RA and 0 degrees Dec.
Midway between the equinoxes, the Sun reaches its furthest north and south. The summer solstice occurs (in the northern hemisphere) around June 21, when the Sun is at 6 hours RA and 23.5 degrees Dec. Around December 21, the Sun is found at 18 hours RA and -23.5 degrees Dec at the winter solstice.
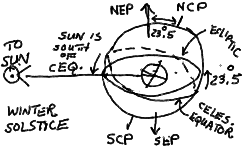
It should be stressed that it is the northward and southward migration of the Sun due to the inclination of the Earth's axis to the orbital axis that causes the seasonal climate that we experience on the Earth. It is not the slightly changing distance from the Sun that the Earth experiences during the year in its elliptical orbit. This change in distance is only about 3%, and in fact the closest approach, known as perihelion, occurs around January 3!
Check out the webpage from Scott Anderson of Emory University illustrating nicely the motion of the Earth. The animations are fairly effective.
Every square meter of the Earth's surface receives a certain amount of sunlight, depending of course upon the time of day and the season. Consider a meter-square solar panel, which will convert the sunlight into electrical energy. Alternatively, we could also consider a meter-square panel of black absorbing material that would turn the sunlight into heat. In any event, when oriented perpendicular to the direction toward the Sun, such a panel will intercept the maximum amount of radiant solar energy. This can be measured as power in Watts --- Joules per second. If we were free of the Earth's atmosphere and had an unobstructed view of the Sun at a distance of 1 AU, we would find that we would intercept a particular flux of energy (in Watts per square meter). This is called the solar constant, and has the value of 1370 W/m^2.
Inclining the panel will reduce the intercepted power by the projected area, or
 )
)
where F is the solar constant, A the panel area, and
 the angle to the perpendicular.
the angle to the perpendicular.
Notice that we could in principle collect all of the Sun's emitted energy by constructing a sphere of radius R= 1 AU enclosing the Sun. Such a sci-fi construction is known as a Dyson sphere and every square meter of its surface would receive a flux equal to the solar constant F. The area of the sphere is 4 Pi R^2, so the Sun must be emitting a power, or luminosity L, of
For F=1370 watts/m^2 and R=1 AU=1.5 × 10^11 m, we find that the solar luminosity
 (1.5 × 1011 m)2 × (1370 W/m2)
= 4 × 1026 W.
(1.5 × 1011 m)2 × (1370 W/m2)
= 4 × 1026 W.
Notice that this relation between flux and luminosity will hold for spheres of any radius
 R2)
R2)
and so the flux falls off as the inverse square of the distance from the source, be it the Sun or a light bulb! For example, the solar flux at the orbit of Mars (R=1.524 AU) will be 0.43 times the solar constant at 1 AU.
© Steven T. Myers 1999
myers@dept.physics.upenn.edu