The volume of the uniform spherical cloud of radius 0.5 pc is
R3 / 3
= 1.54 x 1049 m3
which give a mass density for 250 Msun of
= M / V =
3.25 x 10-17 kg m-3
which for molecular hydrogen H2 gives a number density
/ mH2
= ( 3.25 x 10-17 kg m-3 ) /
( 2 x 1.67 x 10-27 kg ) =
9.73 x 109 m-3
and a total of
hydrogen molecules in the cloud. If each molecule has a thermal energy of 1.5 k T, then the total thermal energy K is
for the cloud. The gravitational potential energy U is
so we compare
vs.
2K = 6.20 x 1037 J
and since -U > 2K we should have gravitational collapse.
Neglecting internal gas pressure, the globule should collapse on the free-fall timescale (derived from an orbit of a=R/2 and P=2t_ff)
2 ( R / 2 )3
==>
( M / Msun ) ( 2 tff / 1 yr )2 =
( R / 2 AU )3
normalized to the Earth's orbit around the Sun, or
which gives
and thus the globule should be the site of star formation in less than 1 million years!
The circular velocity is
so
scaling to the Earth's orbit, or
within the solar circle. The circumference of the solar circle is
R = 1.55 x 1018 km
==> P = ( 1.55 x 1018 km ) / ( 222 km/s )
= 7.05 x 1015 s = 223 x 106 yrs
and thus the Sun makes an orbit of our galaxy every 223 million years. In the current age of the Sun of 4.5 billion years, it has made 20 orbits, and thus our Sun is only 20 G-years old!
You should draw a right triangle with the Sun at the vertex with an angle of 30 degrees between the side Sun-GC and Sun-cloud, and the right angle on the Sun-cloud-GC vertex. With this construction, we see that the distance r of the cloud from the galactic center GC is
for a galactocenter distance R = 8 kpc of the Sun. The projected velocity of the Sun-cloud radial line is equal to the observed velocity of 90 km/s, which is the difference of the projected Sun velocity and the true cloud velocity
(since the line of sight is on the spinward side of the GC) or
for the rotational velocity of the cloud on the 4 kpc circle, which by our above relation means
within the inner 4 kpc of our galaxy.
If you start with all hydrogen (1.007825 amu) and fuse 56 hydrogen to 1 iron
| 56 1H | = 56 x 1.007825 amu = | 56.4382 amu |
| 56Fe | = | 55.8470 amu |
| ___________________________________________ | ||
| 0.5912 amu | ||
or a mass fraction of
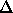m / 56mH =
0.5912 / 56.4382 = 0.0105
and thus 1.05% of the initial hydrogen mass is turned into energy. Or, more usefully for us
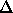m / mFe =
0.5912 / 55.847 = 0.0106
or 1.06% of the resulting mass of Iron was liberated. Therefore, the formation of 0.02 Msun of iron (2% of 1 Msun) gave off
which corresponds to an average luminosity of
over the estimated lifetime of 10^8 years. Note that every 1 Msun of iron out there means 1.91 x 1045 J of energy was released, or 158 Lsun Gyr of energy!
For a recession (Hubble) velocity of 12000 km/s, the distance is
v / H0
= ( 12000 km/s ) / ( 60 km/s/Mpc ) = 200 Mpc
and thus its redshift is
v / c =
( 12000 km/s ) / ( 300000 km/s ) = 0.04
neglecting relativistic and cosmological corrections ( z << 1 ).
Our peculiar velocity of 570 km/s, if it were built up from our Galaxy falling into the potential of the Great Attractor from infinite distance, would be equal to the escape velocity at this distance:
or
and thus the Great Attractor has the mass of several large clusters like Coma!
The luminosity, relative to the Sun (+4.83) is
which is in line with assuming that there are about 10^6 stars in a globular cluster. If the cluster were at a redshift of z=0.1, then its distance is given by the luminosity distance of
= ( 2 c / H0 ) [ (1+z) - (1+z)1/2 ]
(for a critical universe) which gives
which is only 0.2% different than the non-cosmological approximation of
for z = 0.1. The distance modulus should therefore be
and so the globular cluster would have an apparent visual magnitude of
which is within the magnitude range of HST.
We can just go ahead and use our rotation curve - mass relation from Problem 2 again, with new numbers:
within 20 kpc. We then adapt our free-fall time equation from Problem 1 for this mass and a radius of 100 kpc to get
for the estimated formation time for our galaxy. (Note: this problem was particularly easy because we could reuse our scaling relations worked out in previous problems. Whenever you can, derive useful scalings for the quantities from the problem rather than just crunching through it, as you might find something useful in later work.)
The Schwarzschild radius is
and our black hole has a radius of nearly 18 km. Kepler's law
for an orbit of semimajor axis
with a total binary system mass of 12 Msun gives
and thus the timescale for gravity wave emissions from a black hole merger is 12 ms, corresponding to a frequency 1/P = 86 Hz!
The Wien law gives
max =
2.89 x 10-3 m / ( T / 1 K ) = 1.059 x 10-3 m
or just over 1 mm wavelength for the peak of the Cosmic Microwave Background emission. At 1 cm, we are in the Rayleigh-Jeans regime and we can easily compute the intensity
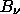
2 k T / 2 =
7.53 x 10-19 W m-2 Hz-1 sr-1
· ( T / 2.728 K ) ( /
1 cm )-2
or 7.53 MJy/sr for the intensity. Over the whole sky (all 4pi steradians, not just the hemisphere of the sky visible from the surface of Earth) this gives a flux density of
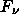= 4
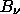= 946 MJy
for the CMB. Note that the Sun is a blackbody with 5770 K and Jupiter with 155 K, so we just need to take the ratio of the solid angles times the temperatures to get the flux densities
==>
= ( 6.96 x 105
/ 1.496 x 108 ) rad = 4.65 x 10-3 rad =
960" = 0.27°
which gives the solid angle
=
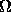2 = 6.80 x 10-5 sr
· ( R / Rsun )2 ( d / 1 AU )-2
and thus for Jupiter ( a = 5.2 AU or d = 4.2 AU from the Earth )
==>
=
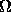6.80 x 10-5 ( 0.1026 )2 ( 4.2 )-2 sr
= 4.06 x 10-8 sr.
The relative flux densities to the all-sky CMB are:
) = 0.0114 Jup: Fjup / Fcmb = ( 155 K / 2.728 K ) ( 4.06 x 10-8 sr / 4
) = 1.84 x 10-7 .
Note that the relative surface brightnesses (intensities) are just given by the ratio of temperatures.
The total flux from the sources is just given by the Stefan-Boltzmann law
d2 ) =
T4 ( R / d )2
or
and so
while the CMB effectively deposits its 3 K worth of radiation evenly over the Earth's entire surface and thus
T4
= 3.14 x 10-6 W m-2
or 3 µW per square meter. (Note that over the entire surface of the Earth, the CMB deposits a total of 1.6 x 10^9 W, or 1.6 GW!)
If we rearrange, the equation becomes
G u /
3c2 ]1/2 dt
where u depends on which case we are dealing with.
Case 1. Matter Domination: In this case we have
c2 =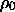 
( R0 / R )3
which after moving the factors of R over to the left-hand side, gives us the equation to solve
G
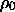/ 3 ]1/2
R03/2 dt =
H0 R03/2 dt
since for a critical universe we have the identity
G / 3 )
= 0
from the energy equation. In any event, we integrate both sides from (t,R) to the current time (t_0,R_0), since we are talking about the late matter-dominated stages, to get
and thus we get the expression
for the look-back time. The time scale depends on the Hubble constant as
if we take t=0 at R=0 under this model (neglecting that eventually the universe becomes radiation dominated).
If recombination occured at a temperature of 3600 K, with a current temperature of 2.73 K, then this must have occured at a scale factor
at a redshift z ~ 1318, which puts it at a lookback time of
or a time after the big-bang of
or 227000 years for h=0.6.
Case 2. Radiation Domination: In this instance we clock versus the temperature directly
which gives
G
a T04 / 3c2 ]1/2
R02 dt =
1.61 x 10-20 s-1 · R02 dt
for T_0 = 2.728 K, which we solve by integrating from (t=0,R=0) to (t,R) to get
or
for the time after the Big Bang.
The Higgs has a mass of 500 GeV / c^2 or an energy of
which corresponds to a thermal energy
which gives the temperature. The scale factor is
z =
( 5.80 x 1015 K / 2.728 K ) =
2.13 x 1015
or a time of
for the universe to have a temperature of the Higgs scale.
We solve
c )
= h / ( Rs c ) = h c2 / ( 2
G m c ) ==> m2 = ( h c ) / ( 2
G )
which gives the Planck mass
G ) ]1/2 =
2.18 x 10-8 kg
which is 10^19 times the proton mass! The corresponding energy scale is
which is reached at a temperature of
at redshift
z =
5.21 x 1031
at a time
for the universe to have a temperature of the Planck scale.