Astronomy 12 - Spring 1999 (S.T. Myers)

Solutions to Problem Set #9

Solutions:

  1. The first step is to rewrite the dynamical equation

    dR / dt = [ 8 G R2 / 3 ]1/2 = [ 8 G 0 / 3 R ]1/2

    and thus

    R1/2 dR = [ 8 G 0 / 3 ]1/2 dt

    is the relation we want. Note, however, that in a flat universe with the critical density that

    H02 = 8 G 0 / 3

    so we can write our differential simply as

    R1/2 dR = H0 dt.

    The integrand becomes

    c dt / R = ( c / H0 ) R-1/2 dR

    which integrates to

    (R) = ( 2 c / H0 ) [ 1 - R1/2 ]

    which you can check by taking the derivative. Substitution of

    R = ( 1 + z )-1

    gives us the expression

    (R) = ( 2 c / H0 ) [ 1 - ( 1 + z )-1/2 ]

    we wanted.

    As z goes to infinity, we get the current horizon distance

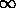    = 2 c / H0 = 6000 h-1 Mpc

    which gives 10000 Mpc for h=0.6 (H0 = 60 km/s/Mpc).

  2. Simple substitution gives

    = ( D H0 / 2 c ) [ 1 - (1+z)-1/2 ]-1 = 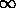(1+z)1/2 / [ (1+z)1/2 - 1 ]

    which tends toward the limiting angular diameter

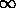    = ( D H0 / 2 c ) = D / 6000 h-1 Mpc
    = 1.667 × 10-4 ( D / 1 h-1 Mpc ) rad
    = 34.4" ( D / 1 h-1 Mpc )

    and our fiducial cluster of D = 1.8 h-1 Mpc tends to the limiting diameter of 61.9 arcseconds (approximately 1 arcminute) at infinite redshift.

  3. Upon substitution we find

    = ( D H0 / 2 c ) (1+z) / [ 1 - (1+z)-1/2 ] = 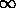(1+z)3/2 / [ (1+z)1/2 - 1 ]

    which now diverges at z = 0 and infinity (try it). Thus, it must be a minimum somewhere in between. If we make the substitution a = (1+z)

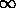    = a3/2 / [ a1/2 - 1 ]

    and the derivative is

    d/da = 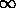3/2 a1/2 / [ a1/2 - 1 ] - 1/2 a / [ a1/2 - 1 ]2

    which when set to zero, and dividing out common factors, gives

    3 a1/2 = a / [ a1/2 - 1 ]

    or

    3 [ a1/2 - 1 ] = a1/2.

    Our solution is then

    a1/2 = 3/2   --->   1 + z = 9/4   --->   z = 5/4

    thus the angular size reaches a minimum at z = 1.25.

    Note: you could also have computed the redshift for which the angular diameter distance dA is a maximum, which is actually more straightforward. Again, with our variable change

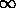    dA = ( 2 c / H0 ) [ ( 1 + z )-1 - ( 1 + z )-3/2 ] = ( a-1 - a-3/2 )

    we set the derivative

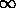    d/da ( dA ) = ( -a-2 + 1.5 a-5/2 ) = a-5/2 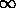( 1.5 - a1/2 )

    equal to zero gives

    1.5 - a1/2 = 0   --->   a1/2 = 3/2   --->   a = 9/4& nbsp; --->   z = 5/4

    as before.

    At the minimum a = 9/4 and thus

    min = 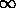27/8 / [ 3/2 - 1 ] = 6.75

    versus the comoving angular diamter at infinte redshift (calculated above).

    Our fiducial galaxy has a size of

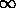    D = 0.1 h-1 Mpc   --->   = 3.44"

    so its minimum apparent angular size is 23.2".

  4. Using

    H0 = 100 h km/s/Mpc / 3.086 × 1019 km/Mpc = 3.240 × 10-18 h s-1

    the current critical density is

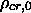    = ( 3 H02 ) / ( 8 G ) = 1.88 × 10-26 h2 kg m-3

    or 2.76 × 1011 h2 Msun Mpc-3. The critical energy density is therefore

    ucr,0 = 1.88 × 10-26 h2 c2 kg m-3 = 1.69 × 10-9 h2 J m-3.

    The radiation constant a (not the scale factor a in the last problem) has the value

    a = 4 / c = 7.56 × 10-16 J m-3 K-4

    which means for T0 = 2.73 K

    urad,0 = 7.56 × 10-16 × 2.734 = 4.20 × 10-14 J m-3

    for the radiation energy density. Thus,

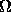    rad,0 = ( 4.20 × 10-14 J m-3 ) / ( 1.69 × 10-9 h2 J m-3 ) = 2.48 × 10-5 h-2

    is the fraction of the critical density currently contributed by radiation.

    Since

    urad / ucr ( 1 + z )4 / ( 1 + z )3 1 + z

    then we will have matter-radiation equality at

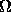    1 + zeq ~ 1 / rad = 4.03 × 104 h2

    and thus the redshift of equality zeq ~ 14500 for h=0.6.

  5. The radial velocity dispersion reprents a 1-D projection of the true 3-D velocities of the galaxies, so

    v2 = 3 r2

    as the squares of the velocities add in quadrature. For Coma

    v = 31/2 r = 1692 km/s.

    The virial relation 2K = -U gives

    2 · (1/2) M v2 = (3/5) G M2 / Rvir

    for mass M and virial radius Rvir. Thus,

    Mvir = (5/3) Rvir v2 / G = 5 Rvir r2 / G

    which for radial velocity dispersion 977 km/s and

    Rvir = 1.8 h-1 Mpc = 5.55 × 1022 h-1 m

    gives us

    Mvir = 3.97 × 1045 h-1 kg = 1.99 × 1015 h-1 Msun

    for the virial mass.

    We use the usual relation between luminosity and absolute magnitude

    log( L/Lsun ) = [ +4.83 - (-26.92) ]/2.5 = 12.7

    for the Sun's absolute visual magnitude of +4.83. Technically, though it wasn't stated in the problem, that since the absolute magnitude is determined from the apparent magnitude and luminosity distance dL (in h-1 Mpc), then the luminosity will be proportional to h2, which gives

    L = 5.01 × 1012 h2 Lsun

    for Coma. Thus,

    M / L = 397 h Msun/Lsun

    for Coma cluster, which is significantly larger than that for the centers of spiral and elliptical galaxies ( ~10 h) and the extended halos of giant elliptical galaxies ( ~100 h). (Note: if you missed the factor of h^2 from the luminosity, thats OK, because I missed it also the first time.)

    If we count up the mass associated with the light which we see, which comes from the galaxies in the cluster, then we would estimate

    Mgal ~ 10 h Msun/Lsun · 5.01 × 1012 h2 Lsun = 5.01 × 1013 h-1 Msun

    which represents a fraction of the total virial (gravitational) mass

    Mgal / Mvir ~ 10 / 397 = 0.052

    and thus 94.8% of the gravitational mass is unaccounted for by the galaxies, and must be dark matter in the extended cluster halo!

  6. The density of the Coma cluster within the virial radius is

    = ( 3 Mvir ) / ( 4 Rvir3 ) = 8.15 × 1013 h2 Msun Mpc-3 = 5.54 × 10-24 h2 kg m-3

    which when compared with

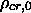    = 1.88 × 10-26 h2 kg m-3

    gives

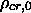    / = 295

    and indeed the Coma cluster is extremely overdense compared to the critical density, and thus should behave like a part of a

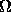    ~ 295 >> 1

    closed universe. Since the density

    R-3   --->   R -1/3   --->   RL 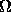1/3 2951/3 = 6.66

    which for R = 1.8 h-1 Mpc gives RL = 12.0 h-1 Mpc. Thus, since the early Universe had a density close to the critical density (as all FRW models do), the Coma cluster has collected up all the matter from a region equivalent to a sphere of radius 12 h^-1 Mpc today!

smyers@nrao.edu   Steven T. Myers