We use the usual relation
so
 2.5 [ 1.15 log( P / 1 day ) + 2.47 ]
2.5 [ 1.15 log( P / 1 day ) + 2.47 ]
or
for the absolute visual magnitude of a Cepheid. The distance modulus
gives
thus for Polaris ( P = 13 days, mv = 2.3 )
or d = 235 pc. Note that the absolute magnitude of Polaris is
with a luminosity of 5611 Lsun!
The mean density
 = ( 3 M ) / ( 4
= ( 3 M ) / ( 4
 R3 )
R3 )
and the period-density relation
 /
(2
/
(2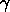 G
G )
]1/2
)
]1/2
give on substitution
 2 R3 ) /
(
2 R3 ) /
( 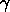 G M ) ]1/2
G M ) ]1/2
or numerically
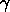 / 4 )-1/2
/ 4 )-1/2
which fills in our table:
| M / Msun | R / Rsun | Mv | P (days) |
|---|---|---|---|
| 5 | 36.3 | -3.1 | 6.925 |
| 10 | 195.0 | -5.9 | 60.96 |
The quantities of interest are:
| log P | Mv |
|---|---|
| 0.840 | -3.1 |
| 1.785 | -5.1 |
and thus we solve the system of equations
-5.9 = 1.785 · a + b
which gives by subtraction
and then
by substitution. Our period-magnitude relation is thus
(which is similar to that used in the previous problem), and
and thus the distance modulus
gives us
and the star is almost 10 kpc away.
To locate Mira on the H-R diagram, we need its luminosity (in Lsun) and its effective temperature. For an absolute magnitude Mbol = -5 and the Sun's bolometric magnitude Mbol = +4.75 we get
Looking at the H-R diagram on p.321 of ZG4 for example, the point
is to the right of the asymptotic giant branch (AGB). Mira must be an evolved star (see also the diagram on p.353 of ZG4).
For the average temperature T = 2300 K, the average radius is
which is in line with it being a late M supergiant. The luminosity ratio is given by the magnitude difference
and so
and the radius changes by a factor of 6 during the pulsation cycle!
For stars of the same luminosity L, they will appear to have a flux
 d2)
d2)
and thus counting the number brighter than some limiting flux f is equivalent to counting the number closer than a limiting distance
 f) ]1/2.
f) ]1/2.
If the stars are distributed uniformly with density n per unit volume, then
 ( f-1/2 )3
( f-1/2 )3
 f-3/2.
f-3/2.
Note that this is true only for a uniform volume density of sources, but is true for any luminosity function of stars.
The circular velocity is given by
 v2 R
v2 R
and since the velocity v is constant
 R
R
is the mass law. For a spherical mass "halo", the mass grows as
 R2
R2
 ==>
==>

 R-2 dM/dr
R-2 dM/dr  R-2
R-2
which is a common profile for the outer parts of massive galaxies and clusters of galaxies. Note you could have also obtained this scaling by

 M / R3
M / R3  R / R3
R / R3
 R-2
R-2
as before.