Astronomy 12 - Spring 1999 (S.T. Myers)

Solutions to Problem Set #6

Solutions:

  1. We get

    L = 4 R2 T4 = Lsun ( R / Rsun )2 ( T / Tsun )4 = 0.0739 Lsun

    or 2.83 x 1025 W.

    We estimate the thermal energy as (for our isothermal white dwarf)

    Uth = N k T = ( M / µmH ) k T = 4.13 x 1037 J

    (for µ=12 Carbon) which will be radiated away in

    tcool ~ ( 4.13 x 1037 J ) / ( 2.83 x 1025 J/s ) = 1.46 x 1012 s = 4.63 x 104 yrs

    at this luminosity. If we include all the scaling dependencies on the assumed parameters, we get

    tcool = 4.63 x 104 yrs · ( T / 30000 K )-3 ( µ / 12 )-1 ( M / Msun ) ( R / 7000 km )-2

    which is convenient for us to calculate at different temperatures. For instance, the cooling time at 109 K is 0.04 seconds! Thus, the White Dwarf cools rapidly at first. The cooling time will not reach 1010 years until the temperature drops to

    T ~ 30000 K · ( 4.63 x 104 yrs / 1010 yrs ) 1/3   = 500 K

    for all other paramters being equal.

    The true cooling rate for white dwarfs is much smaller than our estimate, since they are not isothermal (the cores are much hotter) and the heat conduction and heat capacity must be taken into account! The real cooling times are much longer, and thus old white dwarfs now have temperatures of thousands of K still.

  2. The gravitational binding energy is

    Ugr ~ - G M2 / R = - 5.23 x 1046 · J ( M / 1.4 Msun )2 ( R / 10 km )-1

    for a neutron star. If we include the radius-mass relation

    R = 10 km · ( M / 1.4 Msun )-1/3

    (which gives our 2.8 Msun merged star a radius of 7.94 km) we get the combined energy-mass relation

    Ugr = - 5.23 x 1046 J · ( M / 1.4 Msun )2 ( M / 1.4 Msun )1/3 = - 5.23 x 1046 · ( M / 1.4 Msun )7/3

    so if the binding energy of a lone neutron star is

    U1 = - 5.23 x 1046 J

    then the difference between two lone stars and one merged star of twice the mass is given by

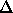    U = 2 U1 - U2 = [ 27/3 - 2 ] U1 = 3.04 U1 = 1.59 x 1047 J

    which can be released in the process.

    To see what we end up with, we note that the resulting neutron star of 7.94 km radius will have a Schwarzschild radius

    Rsw = 2 G M / c2 = 2.96 km · ( M / Msun )

    of 8.3 km. Since it is wholly within its Scharzschild radius, it is (just barely) a Black Hole!

  3. The velocity at a radius R with a rotation period of P is

    v = 2 R / P

    If material is forced to rotate at the same period as the pulsar (the neutron star), then at some radius r_c the velocity v=c. Thus,

    Rcyl = c P / 2 = 1.59 x 106 m

    This radius is known as the light cylinder since within this distance the magnetic field can force gas to rotate with the pulsar. This radius also is an estimate of the sphere of influence of the pulasr.

    To get the binary orbital distance, we use Kepler's 3rd Law as usual

    ( M / Msun) ( P / 1 yr )2 = ( a / 1 AU )3

    so for a total mass of 10.5 + 1.4 = 11.9 Msun, and a period of 2.087 days or P = 5.71 x 10^-3 yrs, we find an orbital radius of

    a = 0.0732 AU = 1.092 x 1010 m

    With a rotation period of 4.84 sec, the light cylinder is

    Rcyl = 2.31 x 108 m

    and so the circular cross-sectional area of the light cylinder is

    Acyl = Rcyl2 = 1.68 x 1017 m2

    for the wind to be intercepted by the pulsar magnetic field. But at the distance a of the pulsar from the star, the wind is being blown into a shell of area

    Awind = a2 = 1.50 x 1021 m2

    and thus only the fraction

    f = Acyl / Awind = 1.12 x 10-4

    of the mass in the wind end up on the neutron star.

    The mass loss rate in the wind emitted from the primary is

    dMwind/dt = 10-8 Msun/yr = 6.34 x 1014 kg/s

    which acts like a mass "luminosity". At the secondary, the mass accretion rate is therefore

    dMacc/dt = 1.12 x 10-4 · 6.34 x 1014 kg/s = 7.10 x 1010 kg/s

    onto the pulsar.

    One kilogram of matter accreted onto the surface from infinity will give off its change in potential energy

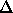    U/m = G M / R = 1.87 x 1016 J/kg · ( M / 1.4 Msun ) ( R / 10 km )-1

    (equivalent to the kinetic energy moving at the escape velocity). Thus, the accretion luminosity is

    Lacc = 1.87 x 1016 J/kg · 7.10 x 1010 kg/s = 1.33 x 1027 J/s (=W)

    or 3.46 Lsun. This is rather modest, but significantly larger than the thermal blackbody emission from the neutron star.

smyers@nrao.edu   Steven T. Myers