The potential at r = 10-15 m is
which corresponds to 1.44 MeV ( 1 eV = 1.602 x 10-19 J ).
For the quantum calculation we solve
 )2 / ( 2µ ) =
kq e2 /
)2 / ( 2µ ) =
kq e2 / 
for  which gives
which gives
 = h2 / ( mp
e2 kq ) = 1.14 x 10-12 m
= h2 / ( mp
e2 kq ) = 1.14 x 10-12 m
which is about 1000 times larger than the nuclear radius used above. In the quantum picture, it is only necessary to bring it close enough to tunnel into the nucleus. The energy scale will be correspondingly lower
with a onset temperature of
which is close to the actual onset of proton-proton fusion in the Sun (about 6 x 106 K).
We combine hydrostatic equilibrium
 /r2
/r2
with mass continuity
 r2
r2

to get the Lagrangian variable formulation
 r4)
==>
P/M
r4)
==>
P/M  M/R4
M/R4
or
 M2/R4
M2/R4
so if

 y
y 
 M2/R4
M2/R4
then

 M / R3 ==> My / R3y
M / R3 ==> My / R3y
 M2/R4
M2/R4
or
 R3y-4
==> R
R3y-4
==> R  M(y-2)/(3y-4)
M(y-2)/(3y-4)
as our radius-mass relation. For degenerate matter y=5/3 so
 M-1/3
M-1/3
as expected. Note that normal matter (an adiabatic gas) has
 M-(x-2/3)/3x x = y - 4/3
M-(x-2/3)/3x x = y - 4/3
which blows up at y=4/3. Other cases:
 M1
M1 y = 2 ==> R
 M0
M0 y = 3 ==> R
 M1/2
M1/2
where the y=1 case is the only physical one (an isothermal gas).
The solar luminosity is 3.83 x 1026 W. Each fusion gives an energy of
which means to sustain the solar luminosity takes 8.93 x 1037 fusions each second. Each fusion converts two protons to two neutrons, and thus makes 2 neutrinos. Thus, the Sun emits 1.79 x 1038 neutrinos each second. At 1 AU = 1.496 x 1011 m, the neutrino flux is therefore 6.35 x 1014 neutrinos s-1 m-2. Most of these solar neutrinos are low energy, and the solar neutrinos carry only about 3% of the solar luminosity.
If one of these neutrinos interacts with an atom in our bodies over the time of 100 years ( 3 x 109 s ), and the physical cross-sectional area of our body is about 1 square meter, then the interaction probability (per neutrino) is approximately the inverse of the number of neutrinos per interaction:
or
which corresponds to a cross-section of 5.25 x 1025 m2 per neutrino.
The 1.4 Msun core has a mass of 2.8 x 1030 kg, of which half is protons (Iron, like most elements, has nearly equal numbers of protons and neutrons in its nucleus). Take 1.4 x 1030 kg of protons at 1.67 x 10-27 kg each and you have 8.38 x 1056 protons. Each of these is squished together with an electron

to produce 8.38 x 1056 neutrinos.
Betelgeuse is 200 pc distant
so we get the neutrino fluence
 ( 6.17 x 1018 m )2 ] =
1.75 x 1018 m-2
( 6.17 x 1018 m )2 ] =
1.75 x 1018 m-2
which with our cross section (or probability) computed above gives
interactions. No problemo.
Note that the Supernova 1987A occured in the Large Magellanic Cloud at a distance of 53000 pc , which gives a neutrino fluence of
 d2
= 2.5 x 1013 m-2
d2
= 2.5 x 1013 m-2
We had 25 trillion supernova neutrinos pass through us on February 24 1987!
At a density of 1012 kg m-3 and a mass of 1.4 Msun ( M = 2.8 x 1030 kg ), the core radius is

 ]1/3 = 8.74 x 105 m
]1/3 = 8.74 x 105 m
or 874 km.
The graviational potential energy is approximately given by
so the change in binding energy is given by
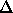 U = G M2 ( 1/Rfin -
1/Rinit ) = ( G M2 / Rfin )
( 1 - Rfin/Rinit )
U = G M2 ( 1/Rfin -
1/Rinit ) = ( G M2 / Rfin )
( 1 - Rfin/Rinit )
which for 874 km collapsing to 10 km gives
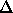 U = 5.23 x 1046 J ·
0.989 = 5.17 x 1046 J
U = 5.23 x 1046 J ·
0.989 = 5.17 x 1046 J
and we get nearly all of the final potential energy out!
The free-fall time t_ff is given by applying Kepler's 3rd law to a radial orbit of semi-major axis a=R/2 and period P=2t_ff:
 2
(r/2)3
2
(r/2)3
or
 2 R3 )
/ ( 8 G M ) ]1/2 = 0.066 s
2 R3 )
/ ( 8 G M ) ]1/2 = 0.066 s
for M=1.4Msun and R = 874km. The core collapses nearly instantaneously!
If the light is 1% of the total energy, then this is equal to 5.17 x 1044 J. If this comes out over 100 days ( 8.64 x 106 sec ) then the luminosity is
At d = 200 pc, this gives an observed flux of
 d2 ) =
0.125 W m-2
d2 ) =
0.125 W m-2
or we can compare the flux directly to that from the Sun by converting the distance to AU
and
and thus the supernova is much fainter than the Sun (on average during this time).