Astronomy 12 - Spring 1999 (S.T. Myers)

1. Because we are first talking about transitions between different electronic energy levels in the same ionization state H I, we use the Boltzmann equation:

   N₂/N₁ = ( g₂/g₁) exp[ -(E₂-E₁)/kT ]

   with statistical weight (the number of states available)

   g_n = 2 n²

   for each level of energy

   E_n = E₀ n^-2.

   Thus, we solve

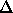   1 = (8/2) exp[ -E₂₁/kT ] = 4 exp( - 118586/T )

   for E₀ = 13.62 eV and

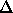   E₂₁ = 13.62 ( 1 - 1/4 ) eV = 10.22 eV.

   We take natural logarithms and rearrange to get

   T = 118586 / ln4 = 85540 K

   for the temperature at which the ground state (n=1) and first excited state (n=2) of H I are equally populated. Note that this temperature is much higher than those found typically in the atmospheres of stars, and thus to good aprroximation we can assume all neutral hydrogen is in the ground state (important later).

   For the ionization states we use the Saha equation:

   N_II/N_I = (0.0333 Pa/ P_e) T^5/2 exp[ -/kT ]

   where the ionization potential from H I to H II is 13.62 eV, or

   /k = 158114 K

   in terms of temperature. So we solve

   1 = (0.0333/2) T^5/2 exp[ -158114/T ]

   or taking base-e logarithms and rearranging gives

   2.5*ln(T) - (158114/T) = ln(2/0.0333) = 4.095

   or

   ln(T) - 1.638 = 63246/T --> T = 63246 / [ ln(T) - 1.638 ]

   which must be solved numerically. Inspection shows the solution should be near 10000 K. Like we did in the past, this equation can be solved by iteration, namely

   T_i+1 = 63246 / [ ln(T_i) - 1.638 ]

   starting with first guess T₁=10000 K:

   i	1	2	3	4	5	6
   Ti	10000	8353	8556	8528	8532	8532

   and although convergence is not super-fast, it does the job. Note that at the moderate T = 8532 K, the H I is half ionized! Thus, by the time we have an appreciable population in the first excited state, most of the atoms are ionized to H II! Thus we are safe with the assumption that for reasonable temperature, all the H I is in the n=1 state.

2. Since we just showed that we can assume all H I is in the ground state, then

   N₂/N = N₂/(N_II + N_I) (N₂/N₁) / (N_II/N_I + 1)

   where

   N₂/N₁ = 4 exp( - 118586/T )

   and

   N_II/N_I = 0.0167 T^5/2 exp( - 158114/T )

   from problem 1.

   To make things easy, we take logarithms

   log(N₂/N) = log(N₂/N₁) - log( 1 + N_II/N_I )

   being careful to go from

   log( 1 + N_II/N_I ) = log[ 1 + 10^{log(N_II/N_I)} ]

   in the final term.

   We crank and tabulate:

   Type	T (K)	log(N2/N1)	log(NII/NI)	log(N2/N)
   G0	6000	-7.98	-3.78	-7.98
   F0	7200	-6.55	-1.67	-6.56
   A0	10400	-4.35	1.66	-6.02
   B0	27000	-1.31	6.76	-8.06

   As expected, we get maximum population (as a fraction of the total number of atoms) in the n=2 level for the A0 star. If we compare to Fig 8-13 of the text (ZG4 p.168) we find that our values for log(N_2/N_1) and log(N_II/N_I) agree, though the curve for log(N_2/N) peaks out at -5 instead of -6 as we found.

   Since the Balmer absorption series are transitions from n=2 to n>2, strength is proportional to the number of atoms in the excited state, and thus should be strongest for A stars.

3. There are 3 ionization states of helium: He I (neutral, 2 electrons), He II (singly ionized, hydrogen-like), and He III (fully ionized). Since we are considering different ionization states, we use the Saha equation

   N_i+1/N_i = (2Z_i+1/Z_i) (0.0333/P_e) T^5/2 exp( -_i/kT )      i=I,II -> II,III

   where we assume P_e = 2 Pa for the electron pressure. The ionization potentials are given:

   _I = 24.5 eV ===> /kT = 284420/T
   _II = 54.4 eV ===> /kT = 631530/T
   

   but the tricky part is getting the partition functions Z:

   He I :	( 2 electrons fill the 2 slots in the ground state )	===>   ZI   = 1
   He II :	( 1 electron for the 2 slots in the ground state )	===>   ZII   = 2
   He III :	( no electrons around the bare nucleus )	===>   ZIII   = 1

   Note that since helium is even more extreme than hydrogen, it is almost certain to be in the ground state!

   We tabulate:

   T (K)	log(NII/NI)	log(NIII/NII)
   100000	10.09	7.98
   150000	10.94	9.33
   200000	11.46	10.10

   Actually, I grossly mis-estimated the interesting temperatures where the ionization transitions occur, and should have asked for:

   T (K)	log(NII/NI)	log(NIII/NII)
   10000	-3.53	-19.21
   20000	3.40	-4.74
   30000	5.90	0.27
   40000	7.24	2.87

   We see that the helium is fully ionized by 40000~K, but will have a maximal population in the doubly ionized state at the crossover around 30000K, and thus the Helium II Balmer series might be present at this temperature. (Try this yourself.)

4. We wish to compute the length X over which

   ~ X = 1

   or

   X = 1 / ( ) = 5.32 x 10^-5 m

   and thus the "mean free path" for the photons in the Sun's core is 53 microns!

5. In a plane-parallel atmosphere with optical depth "tau" at zenith, we get the attenuation

   I = I exp[ - * sec(ZA) ]

   at zenith angle ZA from the vertical, where sec(ZA) = 1/cos(ZA) is also called the airmass since it measures the number of "atmospheres" along the path.

   We have the intensities and magnitudes:

   above the atmosphere :	I = I0	m = m0
   ZA=0°, sec(ZA)=1 :	I = I0 e-	m = 3.0000
   ZA=60°, sec(ZA)=2 :	I = I0 e-2	m = 3.1086

   where we have used sec(60)=2 airmasses. Note that if we take the intensity (or flux, for a given star solid angle) ratio

   I(0°)/I(60°) = e

   while from the magnitude difference we know

   I(0°)/I(60°) = f(0°)/f(60°) = 10^{(3.1086-3.000)/2.5} = 10^0.0434

   and thus

   e = 10^0.0434   ===>   = 0.0434 ln(10) = 0.1

   is the optical depth at zenith. If we then back out the effect of the atmosphere and express this as a magnitude difference dm

   I(space)/I(0°) = e = 10^{(3.000-m0)/2.5}

   but from above this is just

   e = 10^0.0434   ===>   (3.000-m₀)/2.5 = 0.0434  

   or

   m₀ = 3.000 - 0.1086 = 2.8914 mag

   and there is thus 0.1086 magnitudes of attenuation per atmosphere!

   We use the perfect gas law

   P = n k T = kT/µm_H

   to get

   = µm_HP/kT = 1.13 kg m^-3

   and for our optical depth of 0.1

   = 0.1 = X

   we get the opacity

   = 0.1/(X) = 8.9 x 10^-6 m² kg^-1

   for an atmospheric thickness of X = 10 km.

smyers@nrao.edu   Steven T. Myers