Astronomy 12 - Spring 1999 (S.T. Myers)

1. There are different distances in an expanding universe. The comoving distance is the distance measured in units that expand along with the Universe. By following the path of a photon in the Robertson-Walker metric for flat space (k=0), we can obtain the relation

   

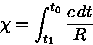
   for the comoving distance. Use the Friedmann equation

   

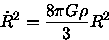
   to find dt, with

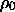   R(z) = R₀ ( 1 + z )^-1       = R^-3

   where R₀ = 1, to obtain the formula

   

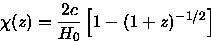
   For H₀ = 100 h km/s/Mpc, what is the comoving distance to the ``big bang'' at z = infinity?

2. A medium-sized cluster of galaxies like the Virgo cluster that we used in the previous problem set has a diameter of D = 1.8 h^-1 Mpc. If this cluster were to keep the same comoving size, ie. it were to expand with the Universe

   D_com = D = 1.8 h^-1 Mpc

   then its angular diameter would be given by the relation

   = D /

   Show that this comoving angular size reaches a finite limiting angular diameter at z = infinty, and calculate this angular diameter for our 1.8 h^-1 comoving Mpc cluster, in arcseconds.

3. Consider now a galaxy of a fixed physical angular diameter of D = 0.1 h^-1 Mpc. This will not in general expand with the universe, and thus in comoving coordinates it will appear to shrink with the scale factor

   D_com = ( 1 + z ) D

   so its apparent size will follow

   = ( 1 + z ) D / = D / d_A

   where we have used this to define the angular diameter distance

   d_A = / ( 1 + z )

   which is true for all cosmologies.

   Show that for our ``flat'' universe from the previous problem

   

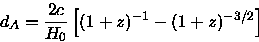
   and thus the apparent angular diameter reaches a minimum value at a finite redshift. Compute these z_min and _min in arcseconds for the galaxy. (Hint: find where d_A is a maximum.) Note that this means that in a flat universe, very distant objects need not appear very small!

4. What is the current critical density for the universe 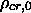in units of h^2 Msun/Mpc^3 for H₀ = 100 h km/s/Mpc?

   Calculate the current critical energy density (equivalent to saying E = mc^2)

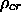   u_cr = c² = 3 H₀² c² / ( 8 G )

   again for H₀ = 100 h km/s/Mpc.

   Calculate the energy density in the cosmic background radiation

   u_rad = a T⁴ = 4 T⁴ / c

   for T₀ = 2.73 K.

   What fraction of the critical density

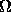   _rad = u_rad / u_cr

   does the cosmic microwave background contribute? (Note: these will be parameterized by h.)

   If density evolves as

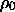   = ( 1 + z )³

   and temperature evolves as

   T = T₀ ( 1 + z ),

   at what redshift z_cr will the energy density of the radiation equal the critical density ( 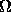_rad = 1 )? Note that this is approximately the redshift where matter and radiation have equal ``densities''. (Hint: this is an estimate, so don't worry about keeping the total energy density equal to the critical density.)

5. The Coma cluster of galaxies is even more impressive than the Virgo cluster, and has a radial velocity dispersion of _r = 977 km/s. What is the true 3-D velocity dispersion of the galaxies _v?

   If the virial radius of the Coma cluster is 1.8 h^-1 Mpc, what is the implied total virial mass of the cluster (in Msun)? Be sure to express this in terms of the Hubble parameter h.

   If the absolute visual magntitude of the Coma cluster is M_V = -26.92, what is the visual luminosity of Coma (in Lsun)? What is the implied mass-to-light ratio of the Coma cluster?

   If an average galaxy in the Coma cluster has a mass-to-light ratio typical of spiral or the centers of normal elliptical galaxies ( ~ 10 Msun/Lsun), what is the total mass of the galaxies in the Coma cluster? Compare this to the total gravitational mass computed above. What fraction of the total mass is in galaxies?

6. We derived the ``cosmic energy equation'' using Newtonian mechanics applied to a uniform universe. In this formulation, we used the fact that only the mass interior to some scale R affects the dynamics. In a sense, therefore, a cluster of galaxies can be thought of a portion of the universe that behaves like a k=1 closed model. Its evolution therefore behaves similarly: it first expands with the Hubble flow, but the gravitational force from its overdensity causes the expansion to turn around, and it then recollapses into the cluster we see today.

   Calculate the density of the Coma cluster _cl (in kg/m^3) using the previously derived mass and the given virial radius. Use this and 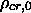calculated above to compute the overdensity of the cluster

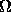   _cl = _cl / .

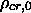   Is the overdensity of the Coma cluster indicative of a piece of a closed universe?

   What would be the radius R_L of the Coma cluster if it has the same mass, but a density equal to 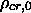(which we assume is the density of the universe for this problem)? This radius R_L is called the Lagrangian radius, and represents the comoving size of the patch of the Universe that collapsed to form the cluster, assuming we began long ago with a nearly uniform universe with only small density perturbations.

Astr12 Index --- Astr12 Home

smyers@nrao.edu Steven T. Myers