The galaxy NGC 2639 is an Sa galaxy with a measured maximum rotational velocity of 324 km/s and an apparent magnitude of B = 12.22 mag (after making corrections for any extinction).
- (a)
- The B-band Tully-Fisher relation for Sa spirals is
MB = -9.95 log vmax + 3.15
- (b)
- Determine the distance to NGC 2639 using its distance modulus .
- (c)
- It is customary to measure a radius R25 to
where a spiral galaxy's surface brightness falls to a level of 25 B-mag/arcsec^2.
Spiral galaxies appear to follow a standard relation
log R25 = -0.249 MB - 4.00
- (d)
- In the B band, the night sky has a brightness of 22 B-mag/arcsec^2. If you want to measure a galaxy profile down to R25 (25 B-mag/arcsec^2), how many times fainter than the sky background is this? This is why its hard to do photometry from the ground.
- (e)
- To measure the mass of a galaxy, we can use Newton's Law (or
Kepler's Law)
v2 = GM / R
- (f)
- The Sun has an absolute visual magnitude of MV = 4.83 and a color index of B - V = 0.64. Find the blue absolute magnitude M_B of the Sun, and use this to determine the luminosity of NGC 2639 in the B band, in Lsun.
- (g)
- Compute the mass-to-light ratio of NGC 2639 in the B band (in Msun/Lsun) interior to R25, using the numbers found above. Is this consistent with what we have learned about spiral galaxies?
The Virgo cluster of galaxies is the nearest substantial cluster. This cluster extends over nearly 10 degrees on the sky, and contains a number of bright galaxies. Our first task is to find the distance to Virgo. The following table gives a list of distance indicators and the results and uncertainties di ± si (mean d, standard deviation s) for the Virgo cluster (adapted from Jacoby et al. 1992). More details on these specific indicators can be found here.
| Method | Virgo Distance (Mpc) |
|---|---|
| 1. Cepheids | 14.9 ± 1.2 |
| 2. Novae | 21.1 ± 3.9 |
| 3. Planetary Nebula Luminosity Function | 15.4 ± 1.1 |
| 4. Globular Cluster Luminosity Function | 18.8 ± 3.8 |
| 5. Surface Brightness Fluctuations | 15.9 ± 0.9 |
| 6. Tully-Fisher relation (spirals) | 15.8 ± 1.5 |
| 7. Faber-Jackson/D-sigma relation (ellipticals) | 16.8 ± 2.4 |
| 8. Type Ia Supernovae | 19.4 ± 5.0 |
Derive an average distance by computing the weighted mean
(di /
i2)
/
(1/i2)
with the sums running over the eight methods i = 1 to 8. Note that this is derived by minimizing chi-squared
=
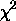( di - D /
i )2
and setting davg = D at the minimum
where d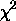/dD = 0.
The uncertainty in our estimator is given by finding where chi-squared increased by 1 above the minimum. This is given by
d2 =
1 /
(1/i2)
assuming the uncertainties really reflect Gaussian errors. What is the uncertainty in our average distance estimate to Virgo, in Mpc?
Spectra of galaxies in the Virgo cluster indicate an average recession velocity of 1136 km/s for the cluster. When combined with the estimated distance from Problem 2, what is the value of the Hubble constant H0, assuming
for the Hubble relation?
Because Virgo represents a significant mass in our corner of the Universe, we must correct the velocity of Virgo for our motion towards the cluster, estimated to be around 168 km/s. What does this correction give us for the value of H0?
Recent parallaxes from the Hipparcos satellite give some indication that our distance scale may be too short, and should be increased by 10%. If we make this correction to our average distance to Virgo, what is the new value of the Hubble constant that we derive?
What is the Hubble time
in years, assuming this value of H0?
The Virgo cluster contains hundreds of galaxies moving around under the influence of its gravitational potential. The radial velocity dispersion of the Virgo cluster galaxies is
r = 666 km/s.
The virial theorem implies
r2
R / G
where the factor 5 comes from assuming Virgo is a uniform density sphere. Using this relation, and assuming that the Virgo cluster is approximately a sphere of radius R = 1.5 Mpc, what is the total gravitational mass of the Virgo cluster, in Msun?
How long, in years, would it take a galaxy to cross
the Virgo cluster? Assume the rms velocity
r.
How does this compare to the Hubble time?
What is the Hubble velocity difference between
opposite points on a diameter of the Virgo cluster?
How does this compare to
r?
How is this (the Hubble velocity over that distance) related to
the timescales we just computed?
Like many large cluster such as Coma, the Virgo cluster contains a hot intergalactic medium (IGM), which is gas at an extreme temperature of 70 million K. This means that Virgo is emitting X-rays via the thermal bremsstrahlung (free-free) process that we discussed in class for the much cooler H II regions.
- (a)
- The luminosity comes from electron-ion interactions,
and can be shown to have an volume emissivity
ff =
1.42 × 10-40
( ne / 1 m-3 )2
( T / 1K )1/2 W/m3.
- (b)
- Again modeling Virgo as a uniform density sphere of radius 1.5 Mpc, what is the total mass (in Msun) of the IGM in the cluster, assuming that it is composed entirely of ionized hydrogen?
- (c)
- What fraction of the gravitational mass is accounted for by the hot IGM?
- (d)
- If the optical luminosity of the galaxies in the cluster give a total of LV = 1.2 × 10^12 Lsun, what is the mass-to-light ratio in the V-band for the Virgo cluster? If an "average" galaxy has a mass-to-light ratio of 10 in V-band, what is the approximate mass in galaxies in the cluster? How does this compare to the hot gas mass of the IGM?
- (e)
- For the IGM gas, the average kinetic thermal
energy per particle is
K = 3 k T / 2
How much energy can we get out of an accreting supermassive black hole? To answer this, we recycle the idea of the Eddington luminosity that we used to calculate the limiting luminosity of a big star:
G M c /
while for electron (Thomson) scattering
= T
/ mH 0.04 m2 kg-1
which is just another way of saying that if the luminosity is too high, then the radiation pressure overcomes the gravitational attraction of the massive object (see Homework Set 4, Problem 3). Calculate the Eddington luminosity for a 10^8 Msun black hole.
The energy comes from the gravitational binding energy of the accreting matter. Derive an expression for the luminosity L of matter accreting at a rate dM/dt (in Msun per year) from infinity to a radius equal to
(a multiple q of the Schwarschild radius ) for our black hole of mass M. Equating this to the Eddington luminosity for our black hole (scale to M / 10^8 Msun, find an expression for the Eddington accretion rate dM/dt(Ed) in terms of q and M / 10^8 Msun. What is the Eddington accretion rate (in Msun per year) for our 10^8 Msun black hole, assuming the gas gets to 3 Rsw (q=3)?
The Eddington accretion rate is the maxiumum rate you can feed a black hole as radiation pressure keeps you from feeding it faster. Furthermore, observations show that active galactic nuclei (AGN) are emitting light at just this rate. Therefore, this is how fast you must be feeding stars into a supermassive black hole in a quasar or radio galaxy to keep it luminous!
