The period-luminosity relationship for classical Cepheid variable stars is
 1.15 ·
log ( P / 1 day ) + 2.47
1.15 ·
log ( P / 1 day ) + 2.47
Use this and the absolute visual magnitude of the Sun (+4.83) to derive a relation between the absolute visual magnitude MV and period P of a Cepheid.
Use the distance modulus to derive the relation between the distance (in pc) and the apparent visual magnitude mv and period P.
Polaris has an apparent visual magnitude of mv = 2.3 and is a Cepheid with a period of P=13 days. What is the absolute visual magnitude of Polaris, and what is its approximate distance in parsecs?
Consider a set of two Cepheid variable stars, with masses, radii, and absolute visual magnitudes as given below:
| M / Msun | R / Rsun | MV | P (days) |
|---|---|---|---|
| 5 | 36.3 | -3.1 | |
| 10 | 195.0 | -5.9 |
Use the period vs. density relationship for pulsating stars
 /
(2
/
(2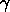 G
G )
]1/2
)
]1/2
with 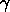 = 4/3,
to calculate the expected periods (in days) and fill in the
table.
= 4/3,
to calculate the expected periods (in days) and fill in the
table.
Assume that Cepheids follow a relationship of the form
and solve for the constants a and b using our calibrator stars given above. (Note that this relation may be different than the one given above!)
We observe a Cepheid variable with a period of 20 days and an apparent visual magnitude of mv = 10.4. What is the distance to the star in parsecs?
The star Mira is a long-period variable (LPV) star with a period of 400 days. The average absolute bolometric of Mira magnitude is Mbol = -5, and the average temperature is 2300 K. What is the radius of Mira (in Rsun)? Where (what branch or sequence) in the H-R diagram does Mira lie? (Note: Mbol,Sun = +4.75.)
During its 400 day period, Mira brightens by 5.1 magnitudes while at the same time its temperature goes from 2000 K to 2600 K. What ratio of maximum to minimum radius does this imply for a radial pulsation?
Consider stars with all the same luminosity L distributed uniformly through space. Show that the number-flux counts follow the relation
 f-3/2
f-3/2
where N( > f ) represents the number of stars visible in the sky with an apparent flux greater or equal to f.
The circular rotation velocity of the disk of our
galaxy is approximately constant at 220 km/s. Use
simple power-law scaling arguments to derive the mass density
law  (r) implied by this
constant rotation velocity with radius from the galactic center.
What is the scaling for the enclosed mass M( < r )?
(r) implied by this
constant rotation velocity with radius from the galactic center.
What is the scaling for the enclosed mass M( < r )?

