For nuclear reactions to occur, two protons must be brought close enough that the {\it Coulomb barrier} between them is overcome. The electric field potential between two charges is

 0r
= kq q1 q2 / r
0r
= kq q1 q2 / r
where k_q = 8.99 x 10^9 N m^2/C^2 is the Coulomb constant. The charge of a proton is e = 1.602 x 10^-19 C. Compute the potential energy in MeV (10^6 eV) between two protons at a separation of r = 10^-15 m, the typical radius of a nucleus.
A better calculation can be done using quantum mechanics. The kinetic energy of two protons collding (in the center of mass frame) is
where µ = m_p/2 is the reduced mass for the two protons (remember our use of this in orbital energies). Quantum mechanics says that we can have fusion if we bring these particles close enough so that one de Broglie wavelength>
 = h / p
= h / p
for momentum p gives a kinetic energy equal to the potential barrier height at that separation
 )2
/ 2µ = kq e2 /
)2
/ 2µ = kq e2 / 
solve this equation for the wavelength (separation of the protons) and thus derive the barrier energy U_q = k_q e^2 / lambda needed to fuse, in MeV.
The average kinetic energy in a gas is given by
Compute the temperature (in K) needed so that
You should understand the derivation of the mass-radius relationship for degenerate matter. Use the equation of hydrostatic equilibrium
 / r2
/ r2
and of mass continuity

 r2
r2
to obtain an expression for dP/dM and thus see how P scales with M and R:
 Ma / Rb
Ma / Rb
where a and b are numerical indexes to be determined from the scaling. Note that you should use the usual scaling dP/dM --> P/M.
If the equation of state of degenerate matter is


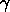
where gamma = 5/3, and

 R3
R3
as usual, then derive the mass-radius relationship for degenerate matter
 M-1/3.
M-1/3.
For amusement, see what happens to these relations for gamma=4/3 and gamma = 2. Try gamma=1 and gamma=3. When faced with a scaling relation you should test its limits.
Assuming every fusion of four protons in the Sun to make one helium nucleus produces two neutrinos, use the observed luminosity of the Sun, and the energy produced in proton-proton fusion, to calculate the number of fusions per second, and thus estimate the number of neutrinos produced in the sun each second. What is the total solar neutrino flux at the Earth (in neutrinos per second per square meter)?
If one solar neutrino will interact with our bodies over our lifetime (a number I read in the book somewhere), estimate the total number of neutrinos that would pass through our body (assume 1 square meter) over 100 years, and thus obtain a conservative estimate of the probability of any one neutrino interacting.
A Type II supernova is caused by the catastophic collapse of the iron core of a star at the end of its life. In that process, all of the remaining protons in the core are converted into neutrons by the weak reaction

as the electrons are squeezed into the protons. Assume that the core mass is 1.4 M_sun (why?), and made entirely of iron. Estimate the total number of protons, and then the total number of neutrinos generated when these protons in the core combine with the electrons to produce neutrons.
Betelgeuse is a bright red star in the shoulder of Orion. It also happens to be a class M2 I supergiant, with a mass of around 20 M_sun, and thus will probably go supernova within the next million years! Betelgeuse is 200 pc from our solar system. Estimate the neutrino fluence (in neutrinos per square meter) at the Earth. Then use the interaction probability computed in the previous problem to estimate the number of these neutrinos expected to interact with our bodies should Betelgeuse blow up! Should we be worried?
Assume that the 1.4 M_sun inert iron core of Betelgeuse is at a mean density of 10^12 kg/m^3, and that the core will collapse to a radius of 10 km. Calculate the total amount of energy (in Joules) produced in the supernova from the change in gravitational binding energy.
Estimate the collapse time, assuming that this occurs on the free-fall timescale. (Hint: Remember, we did this in class. The outer radius will fall in on an orbit that is a line going from the center to the radius of the star, so you can use Kepler's 3rd Law!)
If 1% of the binding energy liberated in a supernova comes out in visible light over the course of 100 days (the time it will take the radiation to get through the stellar debris cloud), what is the average luminosity of the supernova in L_sun?
What is energy flux (in Watts per m^2) in visible light at the surface of the Earth? What is the ratio of this flux to that from the Sun? Will this supernova outshine the Sun in the sky?

