Observations of star forming regions reveal that there are small dense nearly spherical clouds known as Bok globules. A particular Bok globule is observed to have a radius of 0.5 pc and has a total mass (in H2) of 250 Msun. What is the average number density of molecular hydrogen n(H2) in the globule? How many molecules are there total in the globule?
If the thermal energy per molecule of gas is given by 3kT/2, what is the total thermal energy (kinetic energy) K in the globule (in Joules), assuming a cloud temperature of 10 K?
The gravitational binding energy of a uniform density cloud is
Calculate the binding energy U (in Joules) of the Bok globule.
The virial theorem states that for a stable, gravitationally bound system
and therfore if U < 2K then the system has enough gravitational binding energy to collapse (remember U is negative). Would you expect the Bok globule to collapse to form a cluster of stars, or to support itself with gas pressure? If it does collapse, calculate the collapse time (free-fall) in years. If it does not collapse, how massive would it have to be in order to collapse?
The Sun's circular velocity around the center of the Milky Way galaxy is measured to be vc = 220 km/s at its radius of R = 8 kpc. What is the implied mass interior to this radius (in Msun)? How long does it take the Sun to make one revolution about the center of the galaxy? How many revolutions will it have made in the 4.5 Gyr of its life? (This can be thought of as its age in "galactic years".)
Observations of the 21-cm line of hydrogen in a direction 30 degrees from the galactic center (in the same side that the Sun is orbiting toward) show a maximum radial velocity (relative to the Sun) of vr = 90 km/s. This is interpreted to come from an atomic hydrogen cloud moving with its circular velocity away from the Sun at the tangent point (the closest approach along that line of sight to the galactic center). Sketch the geometry of this observation as viewed from far above the disk of the galaxy. Be sure to indicate the position of the Sun, the galactic center, the angle corresponding to the galactic longitude of 30°, and the location of the cloud on the tangent line from us to its circle around the galactic center.
At what radius r from the center of the galaxy is this point?
The measured radial velocity is the difference between the true circular velocity v_c(r) and the component of the Sun's motion in the same direction. Compute the component of the Sun's velocity in this direction, and use it to correct the radial velocity v_r of the cloud to find the true circular velocity v_c(r). What is the implied mass of the galaxy interior to radius r?
This is how the rotation curve of the interior of the galaxy is built up.
During the course of its lifetime on and off the main sequence, a massive star will fuse its hydrogen all the way to iron. If an iron-56 nucleus has a mass of 55.847 amu, what fraction of the mass of the original hydrogen nuclei is turned into energy during the course of this process?
For gas at solar abundance, approximately 2% of it is in heavy elements like iron. Calculate the luminosity in stars corresponding to turning 1 Msun of hydrogen into 1 Msun of gas 2% iron, assuming that the energy liberated is produced over the lifetime of a massive star ~ 108 years.
The Great Attractor is a large cluster or supercluster of galaxies located in the direction of the constellations of Hydra and Centaurus. This region of the Universe is moving away from us with a recession velocity of 12000 km/s. Assuming a Hubble constant of H0 = 60 km/s/Mpc, what is the distance to the Great Attractor in Mpc, and its redshift z?
Our galaxy, and the Local Group of galaxies of which we are part, has been shown to be moving toward the Great Attractor with a peculiar velocity of 570 km/s (measured against the Cosmic Microwave Background). Assuming that we are marginally bound to the Great Attractor (that is, we are moving with the escape velocity), what is the implied mass of the Great Attractor, in Msun.?
The absolute visual magnitude of a bright globular cluster in the Milky Way is Mv ~ -10. What is the approximate luminosity of a globular cluster of this magnitue in Lsun?
What would the apparent visual magnitude of this
globular cluster be if it were at a redshift of
z = 0.1? (Assume H0 = 60 km/s/Mpc and a flat
k=0 universe with 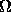 =1.)
=1.)
If our galaxy has a rotation curve that stays flat at a circular velocity of 220 km/s out to R = 20 kpc, what is the mass in Msun enclosed within this radius?
If this enclosed mass collapsed from a sphere that originally had a radius of 100 kpc, how long would it have taken the galaxy to have formed if this collapse occured as free-fall?
If two black holes form a binary system, then they will spiral into each other as the orbital energy is carried away by gravitational waves - the Laser Interferometric Gravity-wave Observatory (LIGO) now being built is designed to search for these systems. What is the Schwarzschild radius of a 6 Msun black hole, in km?
In general, when the black holes orbit decays to around 10 times the Schwarzschild radius, then the black holes will merge together in one orbit or less. What is the orbital period for two 6 Msun black holes orbiting each other at a distance of 10 Schwarzschild radii?
The COBE satellite has determined the temperature of the Cosmic Microwave Background to be
Use the Wien Law for the wavelength of the maximum emission to calculate the peak wavelength of the CMB radiation.
At a wavelength of 1 cm, what is the blackbody
intensity 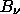 in units of W m-2
Hz-1 sr-1? Since the CMB is isotropic, what
is the total flux density (in W m-2 Hz-1)
over the whole sky? Also, express this in terms of
the normal radio astronomy flux density units of Janskys
( 1 Jy = 10-26 W m-2 Hz-1 ).
in units of W m-2
Hz-1 sr-1? Since the CMB is isotropic, what
is the total flux density (in W m-2 Hz-1)
over the whole sky? Also, express this in terms of
the normal radio astronomy flux density units of Janskys
( 1 Jy = 10-26 W m-2 Hz-1 ).
Compare this flux density to that received from the Sun and Jupiter (T=155 K). (Look up the radius and distance of Jupiter at closest approach to Earth.)
Since the microwave background bathes the Earth in its blackbody radiation (and as a consequence raises the Earth's temperature by 3 K!), this is the one case you can actually use the Stefan-Boltzmann formula to compute the total flux (in W m-2). Do so.
The age of the Universe at any given redshift,
or the time interval between two different redshifts,
depends upon the integral of the expansion rate of the
Universe over this span. In particular, for a critical universe with k=0 and 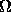 0
=1
0
=1
 G/3c2) u R2
]1/2
G/3c2) u R2
]1/2
where we have used the energy density u instead of the matter density. In the matter-dominated era
 c2
c2
and in the radiation-dominated era
 /c = 7.56 x 10-16
J m-3 K-4 )
/c = 7.56 x 10-16
J m-3 K-4 )
which can be substitued in the dynamical equation
above to obtain the differential equation dt = f(R) dR which in
turn can be integrated to obtain t(R). Use the
evolution of T(R) and  (R)
in terms of the current density
(R)
in terms of the current density  0 and T0, and the definition of scale
factor with redshift
0 and T0, and the definition of scale
factor with redshift
to obtain an numerical expression for t as a funtion of z in these two cases.
The cosmic microwave background was produced at a temperature of
 3600 K
3600 K
when the free electrons finally recombined with the protons and the universe became neutral instead of ionized. Assume that the Universe was matter-dominated and calculate the redshift zrec and the look-back time of recombination ( t0 - trec ). Also estimate the time of recombination after the "big bang" trec under the assumption of matter domination.
At a redshift only a factor of ten higher than that of recombination, the universe was still radiation dominated, as it was at all earlier times. Physicists predict that there is an as-yet undiscovered particle, called the Higgs boson, which is extremely important in setting the masses of the lighter particles. It is expected to have a mass of 500 GeV c2 ( 5 x 1011 eV c2, in energy units ). At what temperature would you expect the Higgs to be created and destroyed regularly in particle-antiparticle pairs (ie. when is kT ~ mc2)?
Compute the corresponding redshift zHiggs and time tHiggs after the Big Bang.
Fo r a summary of particle physics and new particle searches, see http://pdg.lbl.gov/.
Is there a particle that is its own black hole? The Schwarzschild radius for an object of mass m is
and the de Broglie wavelength for asub> relativistic particle of mass m issub>
 = h / m c .
= h / m c .
Calculate the mass mpl for which
 =
=
 Rs
Rs
(the factor of pi is just convention) --- this is known as the Planck mass.
If you have an energy of Epl = mpl c2, you can create a Planck mass particle. At what temperature will the radiation energy of the universe kT be equal to Epl?
At what redshift zpl will the Universe be able to make Planck mass particles at will?
This is a time called the "Planck epoch" and at this earliest stage of the Universe the quantum nature of gravity is important and the notions of space and time as we know them break down. This is effectively the earliest moment of the Big Bang that we can understand.

