Astronomy 11 - Fall 1998 (S.T. Myers)

Solutions to Problem Set #7

Solutions:

  1. The flux ratio versus magnitude difference implies

    m1 - m2 = -2.5 log( f1/f2 )    <==>    f1/f2 = 10(m2-m1)/2.5

    so for a magnitude difference of (-1.5)-6 - -7.5 we find

    a flux ratio of
    fmin/fmax = 10-7.5/2.5= 10-3

    and thus the visible stars range only over a factor of 1000 in brightness.

    Now since the flux is proportional to the distance r^-2, the Sun at 1 AU versus a distance of 10 parsecs = 2062650 AU gives

    m = +4.75 - 2.5 log( 20626502 ) = 4.75 - 5 log(2062650) = 31.57

    and so m = -26.82 for the Sun. Note that this is more than 25 magnitudes or a factor of 10^10 times brighter than the brightest star at night! (Helpful Hint: remember 5 magnitudes is a factor of 100.)

  2. Since for d in parsecs, d=1/p for parallax p in arcseconds, and

    m - M = 5 log(d) - 5 = -5 log(p) - 5

    and for Vega, p=0.1235 (d=8.10pc) gives a distance modulus of m-M=-0.458. Since m=0, then M=0.458 is the absolute magnitude.

  3. Since M=0.458, then

    L / Lsun = 10(4.75-M)/2.5 = 101.7168 = 52.1

    gives the luminosity of Vega.

  4. EPS451 is at a distance of 20pc and thus the distance modulus is

    m - M = 5 log(20) - 5 = 1.505    ==>    M = +7.25 - 1.505 = 5.745

    which in turn gives us

    L / Lsun = 10(4.75-5.745)/2.5 = 10-0.398 = 0.4

    as we got in the previous homework.

    The relevant flux (and thus luminosity ratios) corresponding to the two columns of magnitude differences versus the star are

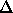    mvis :    Lref/L = 10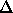mvis/2.5 = A (R/2r)2

    and

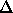    mIR :    Labs/L = 10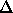mIR/2.5 = (1-A) (R/2r)2

    and thus to get A, we can take the ratio of the ratios, which is equivalent to the differences between the magnitude differences in the table

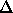    Labs/Lref = = 10(mvis- 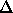mIR)/2.5

    which can be used to compute

    Labs/Lref = (1-A)/A = 1/A - 1    ==>    A = ( 1 + Labs/Lref)-1

    Once we have computed A, it is trivial to substitute that A back in the first relation to get

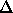    R2 = 4 r2 A-1 10mvis/2.5

    which lets us fill in the empty columns of the table for A and R. Note that getting the equilibrium temperature (now setting G=0) is easy, since

    Teq = 221 K ( r / 1 AU )-1/2 (1-A)1/4

    by suitably modifying the results on the previous homework set.

    We find:

       Orbit       r (AU)       A         R (km)         Teff (K)       probable type of planet          
    1 0.10 0.065 1938 687 Mercury-like?
    2 1.75* 0.35 5400 150 terrestrial
    3 2.5 0.41 7200 122 terrestrial
    4 4.0 0.18 3850 91 terrestrial, icy?
    5 7.0 0.51 64300 70 Jovian (similar to Saturn?)
    6 13 0.62 32850 48 Jovian
    7 25 0.60 18120 35 Jovian
    8 49* 0.50 1365 27 iceworld

    * Note: these two orbital distances somehow got changed from 1.6 and 50 in my notes. Oh well, I'll go with these numbers since that is what I have in my notes...

  5. In the visible band, the brightest planet is #5 with m = 30.5 ( = 7.25 + 23.295 ), which is 0.5 mag fainter than ( 0.63 times ) the HST limit of m=30. Note that in the IR, the brightest is #1 with m = 28.266 which is 1.734 mag brighter or 4.94 times the limit.

    The faintest is #8 at m = 43.158! This is 13.158 mag below the HST limit, or 5.46 x 10^-6 the flux.

    The corresponding limit of Daedalus is given by the ratio of the areas

    ( 25 / 2.4 )2 = 108.51    ==>    2.5 log( 108.51 ) = 5.09 mag    ==>    m = 35.09

    is the new limit. Thus, I am still streching credibility a bit by implying even a 25m telescope could pick up a Pluto around a dim star 20 parsecs away! Not even counting the glare of the star itself...

smyers@nrao.edu   Steven T. Myers