The surface temperature was found to be (HW #3)
where
and
 r2
r2  ]1/4.
]1/4.
For our solar system
Teq = 279 K [ r / 1 AU ]-1/2.
Mars is at r = 1.524 AU so
| Tss | = | 319 K | |
| Teq | = | 226 K | |
| Tsurf | = | 216 K | ( A=0.16, G=0 ) |
The requirement to retain a gas species with a mass per molecule of m is that the escape velocity be greater than 10 times the rms thermal velocity of the molecules:
We normally parameterize the gas by its mean molecular weight a:
Thus, the gas must have a minimum molecular weight
to be retained (we used T=216 K, R=3393 km, M=6.4x10^23 kg for Mars). Note you could have also obtained this by scaling to the equation we derived in class for the Earth:
with T=216 K, M=0.107 M_E, and R=0.53 R_E. In either event, gases with mean molecular weight greater than 21 will be kept, such as N_2 (28), O_2 (32), and CO_2 (44). Mars has only a thin CO_2 atmosphere. I could have a more substantial atmosphere, but doesn't. Another planetary mystery!
Saturn, and thus Titan, is 9.54 AU from the Sun, and so
and
For an assumed A=0.5 and G=0 (thin atmosphere, icy surface) we find
though you might also assumed a thicker atmosphere with A=G, and thus have obtained a surface temperature of 90 K.
For Titan, R=2575 km=0.40 R_E and M=1.34x10^23 kg=0.0225 M_E, so using our scaling from problem 1 versus Earth units
and Titan can easily keep CO_2 (44), O_2 (32), and probably N_2 (28). The organic molecules of H2CO (30) and maybe HCN (27) might also be kept. However, the lighter H2O (18) and CH4 (16) will be lost (probably to Saturn itself!). Note that if you used 90K for the temperature of Titan, you might have found a > 32 and that only CO_2 and possibly O_2 were kept! Note that at this temperature, CO_2 will be frozen onto the surface ("dry ice" like in the Martian polar caps).
Ganymede has R=0.41 R_E and M=0.0248 R_E, but is only 5.2 AU from the Sun so the temperature can be expected to be
| Tss | = | 394 K / [ 5.2 ]1/2 | = 173 K |
| Teq | = | Tss / 21/2 | = 122 K |
| Tsurf | = | 122 K (1 - 0.5)1/4 | = 103 K |
and the condition for gas retention is
and so at best you expect Ganymede to have only CO_2. At these temperatures, CO_2 will be frozen out anyway. Actually, not surprisingly, Ganymede has no discernable atmosphere.
(a) The moments of inertia (Earth=E and Lunar=L) are
IL = 0.4 ML RL2 = 8.82 x 1034 kg m2
and the angular frequencies are
 E =
2
E =
2 /PE
= 7.27 x 10-5 rad/sec
/PE
= 7.27 x 10-5 rad/sec  L =
2
L =
2 /PL
= 7.27 x 10-5 rad/sec
/PL
= 7.27 x 10-5 rad/sec
for a (sidereal) rotation period of the Earth of 24 hours and of the Moon of 27.3 days. Thus, the rotational angular momenta are
 E
= 7.06 x 1033 kg m2 / sec
E
= 7.06 x 1033 kg m2 / sec LL = IL
 L
= 2.35 x 1029 kg m2 / sec
L
= 2.35 x 1029 kg m2 / sec
and thus L_E = 3 x 10^4 that of the Moon! The orbital angular momentum is given by
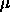
 orb a2
= 2.82 x 1034 kg m2 / sec
orb a2
= 2.82 x 1034 kg m2 / sec
for a = 384000 km and reduced mass
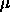 =
(MEML)/(ME + ML) =
ML/(1+ ML/ME) =
7.2 x 1022 kg
=
(MEML)/(ME + ML) =
ML/(1+ ML/ME) =
7.2 x 1022 kg  ML
ML
and is four times the Earth's rotational angular momentum! The total angular momentum of the system is approximately (remember that the Earth's rotation axis is aligned 23.5 deg to the ecliptic, and the Moon's orbit 5 deg to the ecliptic, and thus there is at least an 18 deg mismatch)
 7.06 x 1033
+ 2.35 x 1029 + 2.82 x 1034
= 3.53 x 1034 kg m2 / sec
7.06 x 1033
+ 2.35 x 1029 + 2.82 x 1034
= 3.53 x 1034 kg m2 / sec
with 80% in the orbital term and only 20% in the rotational terms (mostly the Earth's).
(b) We can write, when all three frequencies are equal
 + Lorb
+ Lorb
with
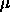
 a2 =
a2 =
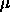
 [ G M /
[ G M /  2 ]2/3
=
2 ]2/3
= 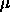 [ G M ]2/3
[ G M ]2/3
 -1/3
-1/3 = 3.93 x 1032
 -1/3
-1/3
which gives
 + 3.93 x 1032
+ 3.93 x 1032  -1/3
= 3.53 x 1034.
-1/3
= 3.53 x 1034.
(c) We want to solve the equation
 + J
+ J  -1/3.
-1/3.
with
I = 9.72 x 1037
J = 3.93 x 1032
(remember omega is small). You can think of this as a fourth order equation
 1/3)
1/3)
and thus it actually has two solutions! Dynamically, remaining rotational angular momentum (in the I-term) is being tidally transferred into the orbit (J-term), keeping the total angular momentum L conserved! Note that there is a limit on how far the angular frequency can drop, that is that due to the presence of some residual rotation, it can never get so far as ALL of the momentum is in the orbit
 min = [ J / L ]3
= 1.38 x 10-6 rad/sec --> P = 52.7 days.
min = [ J / L ]3
= 1.38 x 10-6 rad/sec --> P = 52.7 days.
The solution we want is a small perturbation on this. This suggests the procedure of iteration, where we start with a guess, and perturb it toward the real solution. We want to isolate the dominant J-term to a constant, which suggests the substitution
 -1/3
-1/3
which gives
where as expected the solution should be near x = L/J = 90, and the second term is small. Numerically,
and so we set up our iteration from step i
to get estimate for i+1. If we start with our guess of x = 89.8, we see this converges very quickly
| i | xi | |
|---|---|---|
| ___ | _______ | |
| 0 | 89.80 | first guess |
| 1 | 89.46 | |
| 2 | 89.45 | converging |
| 3 | 89.45 | converged! |
As expected, this converged quickly to
 = x-3 = 1.40 x 10-6
rad/sec --> P = 52.0 days
= x-3 = 1.40 x 10-6
rad/sec --> P = 52.0 days
which is pretty close to our estimate anyway! Note that some of you might have been fooled into getting the other solution, where all the angular momentum is in the rotation
 = L/I - J/I
= L/I - J/I
 -1/3
-1/3
which should have a solution near

 L/I
= 3.45 x 10-4 --> P = 0.21 days
L/I
= 3.45 x 10-4 --> P = 0.21 days
which is a fast rotation (and orbit) indeed! See if you can solve this iteratively ...