Astronomy 11 - Fall 1998 (S.T. Myers)

1. The important facts given were that local noon is defined as the time when the Sun is on the observer's local meridian, and that at that moment the Local Sidereal Time happened to be 12h LST. Since LST is defined as the Right Ascension (RA) that happens to be on the local meridian, this question is really asking "on what date is the Sun at RA = 12 h?".

   In case you forgot, or were confused, the meridian is the line (great circle) the passes through the zenith (overhead) and the North and South points of the horizon, and is thus an extenison of the longitude line of the observer. Since RA circles are concentric with longitude lines, as the Earth turns consecutive RAs pass overhead each observer, and thus define a "clock" - the sidereal clock which keeps Local Sidereal Time.

   To figure out when the Sun is at RA=12h, you need to know the zero-point of Right Ascension: the Vernal Equinox is RA = 0h, Dec = 0°. The Sun is at the Vernal Equinox on March 21, and thus the Sun is at RA = 12 h (and also Dec = 0°) 6 months later at the Autumnal Equinox, around Sep 21.

   The Sun moves along the ecliptic a full 24 hours in 12 months, at the average rate of 2 hours per month. Since the Earth rotates in the same sense as it orbits the Sun, the Sun appears to advance along in positive RA, and reaches an apparent RA = 6h around June 22 (Summer Solstice) and RA = 18h around Dec 22 (Winter Solstice).

   You can thus compute the RA of the Sun on your birthday by offsetting from these points. For example, my birthday is May 22, which is just about 2 months after the Vernal Equinox, and thus the Sun is at

   RA (May 22) = 0h (Mar 21) + 2h x 2 (months) = 4 h

   which gives the LST at local noon on that date, as we pointed out above.

2. This calculation is extremely straightforward. We use the Newtonian version of Kepler's Third Law

   G M P² = 4 ² a³

   where everything should be in MKS units (be sure to convert km to m for example). Thus, we can rearrange this to solve for the mass

   M = ( 4 ² a³ ) / ( G P² ).

   For Deimos a = 2.352 x 10^7 m, P = 108864 sec, and as usual G = 6.67 X 10^-11 N m^2/kg^2, so

   M = 6.5 x 10²³ kg = 0.109 M_earth

   for an Earth mass of 6 x 10^24 kg.

3. At perihelion and aphelion, the velocity vector v is perpendicular to the radius vector r, so the conservation of the angular momentum per unit mass gives

   H = v r = v_p r_p = v_a r_a

   which implies

   v_p / v_a = r_a / r_p.

   Thus,

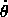   _p / 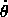_a = ( v_p/r_p ) / ( v_a/r_a) = ( r_a / r_p )²

   which for

   r_p = a ( 1 - e ) ; r_a = a ( 1 + e )

   gives

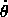   _p / 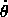_a = ( 1 - e / 1 + e )² = 1.452

   for the eccentricity e=0.093 of Mars.

   Now, by the average angular velocity I merely meant that it moved a full 360° along the Martian ecliptic in one full sidereal period (686.98 days from Appendix 3). Thus, the "average" rate of advance is

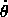   _avg = 360° / P = 360° / 686.98d = 0.524 °/d

   which is about half the solar advance rate as seen from the Earth (360° in 365.26 days).

   Note: you could also have obtained this by

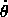   _avg = v_circ / a ( 2 a / P ) / a = 2 / P

   radians per day.

4. You should definitely draw a picture for this one. The transfer orbit from Earth to Mars as a perihelion of 1 AU and aphelion of 1.524 AU, and so the semimajor axis of the transfer orbit is

   r_p + r_a = 2 a => a = ( 1 AU + 1.524 AU ) / 2 = 1.262 AU.

   The eccentricity is given by

   r_p = a ( 1 - e ) => e = 1 - r_p/a = 1 - 1/1.262 = 0.208.

   The relevant circular velocity of the Earth's orbit is

   v_circ,E = [ G M_sun / a ]^1/2 = 29800 m/s = 29.8 km/s

   for a = 1 AU = 1.5 x 10^11 km and Msun = 2 x 10^30 kg. Now, it is useful to scale to this

   v_circ = 29.8 km/s / (a / 1 AU )^1/2

   which gives

   v_circ,M = 24.1 km/s ( a = 1.524 AU )
   v_circ,tr = 26.5 km/s ( a = 1.262 AU )

   for Mars and the "transfer orbit" respectively. (Note: we computed the circular velocity at the semimajor axis of the tranfer orbit for ease of computing the next bits. Its good to think ahead.

   Now, we know from class (and Eq 1-17 of the textbook) that

   v_p = ( 2 a / P ) [ 1+e / 1-e ]^1/2

   but since

   2 a / P = v_circ

   and

   ( 1+e / 1-e ) = r_a / r_p

   then we can rewrite this as

   v_p = v_circ [ r_a / r_p ]^1/2

   and so

   v_p = 26.5 km/s [ 1.524 / 1 ]^1/2 = 32.7 km/s

   for our transfer orbit. Therefore, we have to "inject" it from Earth's orbit with an extra velocity

   v_inj = v_p - v_circ,E = 32.7 - 29.8 = 2.9 km/s.

   For the aphelion, we have

   v_p = ( 2 a / P ) [ 1-e / 1+e ]^1/2 = v_circ [ r_p / r_a ]^1/2

   and so

   v_a = 26.5 km/s [ 1 / 1.524 ]^1/2 = 21.5 km/s

   for the transfer orbit. Thus, we need to add a further "retro" velocity

   v_ret = v_circ,M - v_a = 24.1 - 21.5 = 2.6 km/s

   to move from the transfer orbit into a Martian circular orbit around the Sun.

   Note that we need to add velocity both times, since we are going into respectively higher energy orbits

   E = - G M_sun / 2a

   which become less negative (less bound, higher energy) as a increases.

   Note also that we saved some work by playing with the equations for v_p and v_a in terms of v_circ and r_a/r_p before pluggin and chugging!

smyers@nrao.edu   Steven T. Myers