Mars has only a very thin atmosphere, but is otherwise similar to the Earth. It is somewhat smaller, so maybe it couldn't hold a bigger atmosphere. Calculate the expected surface temperature of Mars, and then use this to find the minimum molecular weight a of a gas that can be retained over a billion years of time. Which gases would have escaped? Does this explain why Mars has such a thin atmosphere?
Observations from the Voyager mission show that Titan, the largest moon of Saturn, has an atmosphere! Use the condition for retention of a gas in the atmosphere over the course of a few billion years (the age of the planets) to find the minimum molecular weight a of a gas that could be in this atmosphere. The building blocks of simple amino acids are methane (CH_4), water (H_2 O), carbon dioxide (CO_2), formaldehyde (H_2 CO), and hydrogen cyanide (HCN). Compute the molecular weights of these molecules and determine whether they would be retained on Titan. (You can find the physical parameters of Titan in the appendix of the text, and you may have to make a guess on some other properties - be sure to justify these.)
Ganymede, the satellite of Jupiter, is the largest moon in our solar system. Would you expect it to have an atmosphere?
The angular momentum of a spherical rotating body is given by

where I is the moment of inertia and  is
the angular frequency in radians/sec, with
is
the angular frequency in radians/sec, with
 = 2
= 2  / P.
/ P.
For a sphere,
The orbital angular momentum of a two body system with semimajor axis a and eccentricity e we had showed to be
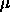 [ GMa
(1-e2) ]1/2
--->
Lorb =
[ GMa
(1-e2) ]1/2
--->
Lorb = 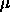 [ GMa
]1/2 =
[ GMa
]1/2 = 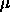
 a2
a2
where we have assumed a nearly circular orbit e=0. Remember that the reduced mass
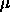 = ( m1 m2 ) /
( m1 + m2 ).
= ( m1 m2 ) /
( m1 + m2 ).
A third relation of use is Kepler's Third Law
 2 a3
--->
2 a3
--->
 2 =
4
2 =
4 2 / P2 =
G M a-3
2 / P2 =
G M a-3
which we used partly to arrive at the final expression for L_orb above.
(a) Compute the rotational angular momenta L_rot of the Earth and the Moon (get the masses, radii, and rotational periods from the textbook). Then, compute the orbital angular momentum L_orb of the Earth-Moon system. Compare the two: which component dominates the angular momentum of the Earth-Moon system now? Since the rotational and orbital axes are approximately aligned, sum the three to get the total angular momentum of the Earth-Moon system L_tot = L_rot + L_orb.
(b) The tidal locking effect will eventually increase the Earth's rotational period and lengthen the Moon's rotational and orbital periods so that all three are equal. To compute the evolution of the orbit and rotation, we need to arrive at an expression for L_tot which only depends on one of the variables a and w ("omega"). Use Kepler's 3rd Law above to substitute in for a in L_orb so you have an expression that only depends on w and thus derive an equation for L_tot (which will have three terms for the rotation of the Earth, rotation of the moon, and the relative orbit) as a function of w.
(c) Use conservation of the total angular momentum and the current
total angular momentum from part (a), and the equation you derived in part (b),
to find the final equilibrium value of
 eq
and thus the period P_eq. (Hint: if you have trouble solving the equation,
just use the
dominant term and assume all of the initial angular momentum is transferred
into that. You should get a final period in the neighborhood of 50 days.)
eq
and thus the period P_eq. (Hint: if you have trouble solving the equation,
just use the
dominant term and assume all of the initial angular momentum is transferred
into that. You should get a final period in the neighborhood of 50 days.)
Hints: You should end up in (b) with an equation of the form
 +
b
+
b  -1/3
-1/3
where the a term represents the rotational component and the b term the orbital component. Note that as w drops, the a term gets smaller and the b term gets bigger. This equation looks hard to solve, but it really isnt. First of all, there are two solutions, one with small w and one with big w. Which one do we want? Obviously, the small w is a fast rotating solution with a small orbital radius. Thus we want the large w solution for slow rotation and large orbit! This means the first a term will be negligible, and you can get pretty close just by ignoring that term and solving
 b
b  -1/3
-1/3
which was what I was getting at in the explanation for 3c. On the other hand, if you really want to truly solve the equation, you can use a technique known as iteration. You know that you are looking for a perturbation around the solution above, so first make the substitution
 -1/3
-1/3
so our equation is equivalent to
and then rearrange this to get the form
where of course you have to work out what a, b and A, B really are! Note that the approximate solution from above is just x=A. Now if you have a guess w_i at iteration i, you can use this to get a refined guess w_(i+1)
which hopefully should converge to the correct value (it will). As a starting guess, use the approximate value you got by ignoring the first term (x_1 = A)! Iteration is an incredibly useful numerical technique for solving odd looking algebraic equations, though you may have to reformat the equation to make it converge (eg. how would you make it converge to the large w solution?). If you are still unconvinced (or interested in why the method works, look at it graphically: plot y=x and y=A - Bx^-3, and see how the iteration jumps between these curves. I'm sure this is all more than you wanted to know, but think of this as extra bonus knowledge!

