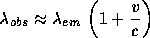
| Gravitational Lenses and Cosmology: | |
| A Cosmological Primer: | |
Cosmology as a field of astrophysics is concerned with (in the words of Hawking and Ellis) the large-scale structure of spacetime. When related to astronomical observations (such as the gravitational lensing, distant supernovae and galaxies that are discussed in these articles), cosmology relates the times, distances, brightnesses, and angular sizes of observed objects to the overall geometry, topology, matter and energy content in the Universe, and the time evolution of these quantities.
The fundamental observation of cosmology occured at the start of this century: Edwin Hubble's discovery of the expansion of the Universe exhibited by his famous distance - velocity relation
where H0 represents the Hubble Constant in the curious units of km·sec-1·Mpc-1. (Note: 1 megaparsec, or Mpc, is equivalent to one million parsecs, where 1 parsec, or pc, is 206265 times the average Earth-Sun distance, or 3.086 x 1013 km, or 3.26 light-years.) Current estimates of the Hubble constant cover the range of 45 < H0 < 75 km·sec-1·Mpc-1 [see main article, Myers, S. T. (1999) Proc. Natl. Acad. Sci. USA 96(8), 4236-4239]. It is customary to parameterize our uncertainty in the value of the Hubble constant by
and thus other cosmological quantities that depend upon the Hubble constant will contain factors of h as appropriate.
The "Hubble velocities" in the above relation are determined by observing the Doppler shift
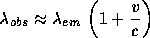
for an electromagnetic wave emitted from an object receding from
the observer at velocity v. Of course, in the expanding universe
model, it is space that is growing, and the observed velocities are
due to this increasing.
The light from an object emitted at rest wavelength
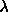em at time t and observed now
at t0 will be Doppler-shifted to a longer wavelength
,
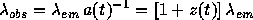where a is the scale factor normalized to the current scale
and thus
defines the redshift of the object in terms of the scale factor. In addition to a measure of time, the redshift is the primary cosmological distance indicator. For a complete discussion of cosmology in the context of general relativity and the cosmography of the Universe, see the texts [A1] and [A2]. In addition to distances, z(t) gives us the age of the Universe as a function of redshift, with best estimates of the current age being 9-15 Gyr.
There are a number of parameters that go into the cosmological model that relate the distances, redshifts, and times at which observed phenomena (which are seen by the light they emit or absorb) are seen to occur. As mentioned above, the Hubble constant H0 is a measure of the current expansion rate of the scale factor a, with
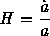
and the second time derivative gives the acceleration or deceleration of the Universe
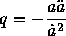
where its current value is q0. In turn the question of whether the expansion is accelerating q0 < 0 or decelerating q0 > 0 depends upon the mean density of matter and energy in the Universe. The density parameter
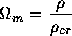
refers to the fraction of the mass-energy density in the Universe as a fraction of the critical value
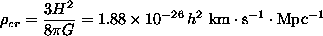
that will asymptotically bring the expansion to a halt in the
infinite future, with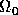 
again denoting its
current value. In a cosmology with no cosmological constant, the
deceleration parameter takes on a value equal to one-half the density
parameter, and so q0 = 0.5 denotes a critical Universe.
Furthermore, the density parameter can be related to the topology of the Universe, which is determined by the sum of the mass-energy densities in matter and in any possible cosmological constant
.
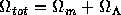A popular suite of cosmologicals has a globally flat Universe
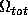= 1, with a subcritical matter density
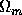< 1 and the remainder taken up in vaccuum energy
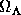= 1 - 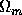> 0.
Technically, this missing energy -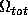
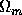could be in the form of matter with an
arbitrary equation of state. This has
been recently considered in the context of inflationary cosmological models
[A3]. We return to the question of
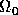and the
missing energy problem when we discuss cosmological constraints from
lens surveys.
The real key to understanding how the cosmology affects what we observe for a given gravitational lens is how we actually go about measuring distances in the Universe. We are used to dealing with Euclidean distances in a locally flat geomtery, and are taught that, for example
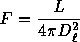
gives the observed flux F for true luminosity L at distance Dl, and
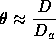
tells us the angle subtended by a distant an object with physical diameter D at distance Da. Technically, the subscripted distance measures Dl and Da are the luminosity distance and angular diameter distance respectively. Normally, we don't worry about which distance we are talking about, but in the curved spacetime and expanding Universe of cosmology these are not the same! For so-called Freidmann, Robertson, Walker (FRW) cosmologies, which are solutions to the General Relativistic equations of motion in a homogeneous and isotropic Universe, we have
The angular diameter distance Da, which as we will see
is fundamental to gravitational lensing, depends in turn upon the
redshift with a functional form that depends upon the matter
and cosmological constant density parameters. The simplest forms are
for Universe models without cosmolgical constants
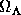( = 0). For example, in an empty
Universe, which has a constant rate of expansion (q0
= 0), we have the particularly simple form
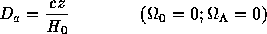
for the distance-redshift relation. At the other extreme, we have for a Universe with the critical density
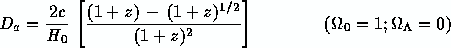
in which the expansion will decelerate (q0 = 0.5) asymptotically to a halt in the infinite future. Note that in this model the apparent angular size of an object with a fixed physical diameter D will decrease to a minimum at a finite redshift zmin = 1.25, and then will appear to grow larger at higher redshifts (this is just due to the light rays emitted by the ends of the diameter D propagating through the ever slowing expansion of the Universe). Thus, in this model, the inverse function of redshift given angular diameter distance is double-valued. Note that all distances for all models tend toward the simple expression given above for the empty Universe in the limit of small redshift z << 1. Furthermore, all distances are inversely proportional to the Hubble constant, e.g.
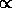H0-1
again for all models. This is the fundamental property of distances we will exploit in determining the Hubble constant from lens observations.
| Users Guide to Gravitational Lensing: | ||
The phenomenon of gravitational lensing is closely related to the gravitational deflection of light rays passing close to a massive body like the Sun. The deflection angle is given by the ratio of the Schwarzschild radius (the radius of a black hole of equivalent mass) to the impact parameter of the light ray
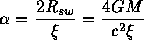
which for our Sun translates to an angle of 1.76 arc-seconds for a ray grazing the solar limb. In fact, as the factor of 2 in the deflection is due to the general relativistic effect of the gravitational potential, the observation of the deflection angle in 1917 was heralded as a triumph of Einstein's theory over classical Newtonian gravity.
Figure 1 shows the lensing geometry for a typical double-image lens. If the mass distribution, and thus the gravitational potential, is axisymmetric, then the images, lens, source, and observer all lie in the same plane as in the figure.
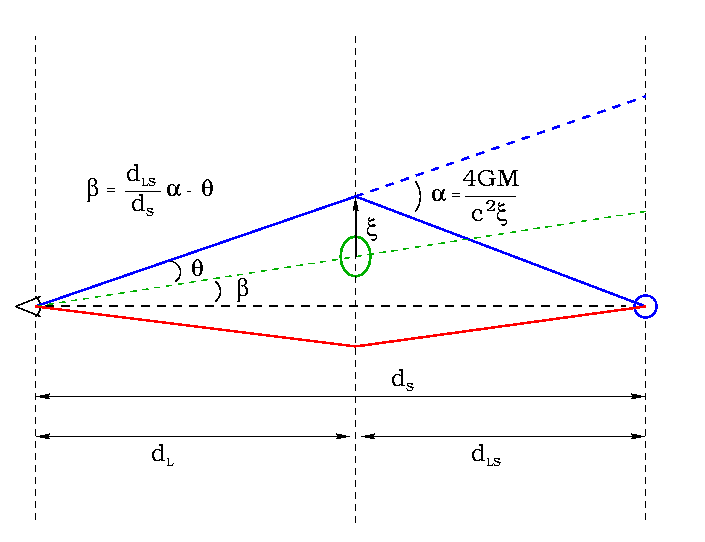
Figure 1. Schematic of image formation by an axisymmetric surface mass distribution. Two images are formed by light rays traveling on the blue and red paths. The blue path is geometrically longer than the red path with respect to the undeviated path directly from the observer at left to the source at right, and also goes through a deeper part of the gravitational potential of the lens. Therefore, the image corresponding to the blue path will be delayed by a fixed amount relative to wavefronts arriving from the image along the red path.
For a general extended distribution of mass, it is the surface
mass density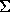 
that takes the place of the mass
M in the lens equation. The deflection angle
will then be proportional to the integral over
the impact parameter in the ``lens-plane'' of the surface mass divided by the
impact parameter with the ray
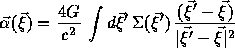
where we have written this in angular vector form to deal with non-axisymmetric mass distributions. Deflecting mass distributions with significant ellipticity will be able to produce image configurations with more than two components (e.g., ``quad'' lenses such as CLASS B1608 + 656). The lensing equation then becomes
,
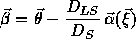where the distances DLS and DS are the angular-diameter distances from the lens to the background source and from the observer to the background source respectively. The third distance is DL from the observer to the lens, and in an expanding universe
.
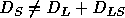The Hubble constant enters through the distances D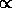
H0-1. Note that
any ratio of two distances will be independent of the Hubble constant.
It turns out to be possible to reduce the lensing equation to the deceptively simple form
,
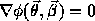where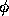 
is the Fermat potential. Images therefore
form at the extrema of the Fermat potential (the minima, maxima,
and saddle-points), and the time delay between any two images is
related to the difference in the potential
,
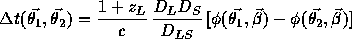which is proportional to H0-1, but only weakly dependent on other cosmological factors such as the density parameter, through the ratio of the three angular-diameter distance factors. The mass is absorbed into the potential terms. While direct observations of the image positions and relative magnifications can only effectively constrain the Fermat potential (a ratio of mass to distance), the measurement of the time delay can break the degeneracy and yield the Hubble constant.
| Bestiary of Gravitational Lenses: | ||
As of early 1999, there are still relatively few gravitational lens systems that have been monitored for variability, and have produced a reasonably robust determination of the Hubble constant. These are the five systems B0957 + 561, B0218 + 357, PG 1115 + 080, CLASS B1608 + 656, and most recently PKS 1830 - 211. All but the last were described in the main article, and further images are linked below.
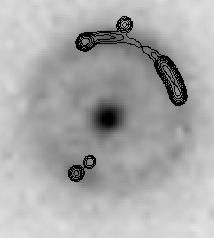
B0957 + 561: This is the original gravitational lens, and has two images of the background quasar separated by 6.1 arc-seconds.
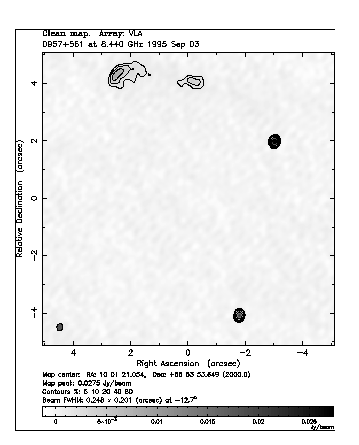
Figure 2. VLA X-band image of lens B0957 + 561, taken during the CLASS observations. The two compact images are seen, as well as some of the extended jet emission curving away to the northeast. Most of the jet emission has been resolved out by the high resolution interferometry of the VLA in its A-configuration. (Courtesy CLASS.)
B0218 + 357: This gravitational lens system, which was discovered as part of JVAS, consists of two compact radio components separated by 0.335 arc-seconds and an Einstein ring.
PG 1115 + 080: The second lens system to be discovered, this system consists of four optical images of a z = 1.722 QSO.
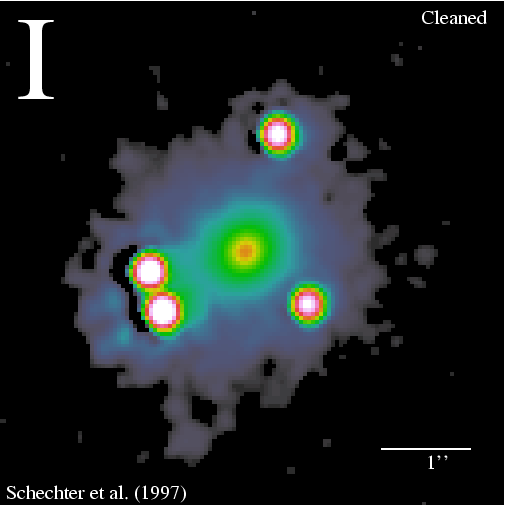
Figure 3. Optical I-band image of lens PG 1115 + 080, showing the four quasar images plus the lensing galaxy. (Courtesy Paul Schechter, CASTLES.)
CLASS B1608 + 656: This system has four compact radio components, as well as an infrared Einstein ring. The image geometry and flux ratios are not well fit by a single-lens model, and HST images show the lensing galaxy to have two brightness centers, consistent with it being a binary galaxy lens [A4].
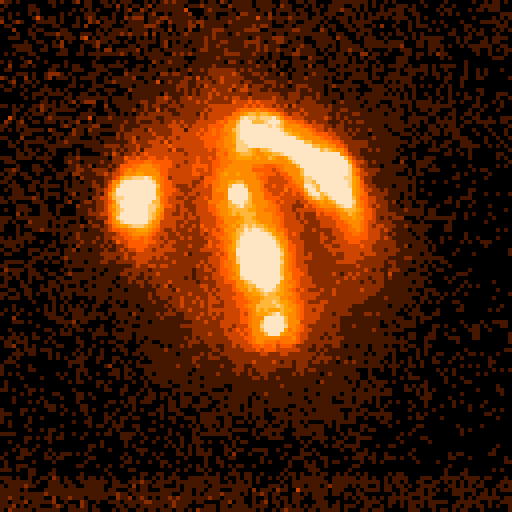
Figure 4. HST NICMOS image of lens CLASS B1608 + 656, showing the binary nature of the lens light distribution, as well as the four images plus the Einstein ring. (Courtesy Chris Fassnacht, NRAO.)
PKS 1830 - 211: For example, the lens system PKS 1830 - 211 (a flat spectrum double with moderate flux ratio located on opposite sides of a 1 arc-second diameter Einstein ring) has recently yielded a time delay of 26 (+4, -5) days [A5], but no H0 estimate was possible since the AGN redshift was not known at the time that this article went to press. However, very recently, a redshift of z = 2.507 was found for the background source [A6], which leads to a value for the Hubble constant of
= 1)
or
= 0.3)
and thus this system becomes the fifth lens to produce a solid Hubble constant determination.
Below is shown perhaps the best example of gravitational lensing with a nearly complete Einstein ring. The JVAS lens B1938 + 666 [A7] shows both compact multiple images and extended arcs in the high-resolution radio image taken by the MERLIN interferometer. The HST infrared NICMOS image, on the other hand, shows the lensing galaxy plus the background galaxy distorted into a circular annulus. This is an example of a lens system with nearly perfectly alignment along the observer lens source axis! Should the compact components prove to be variable, the large number of constraints upon the lens gravitational potential by the arcs and ring would make this an important system for cosmology.
 |
 |
Figure 5. The spectacular Einstein ring source JVAS B1938 + 666, as seen by MERLIN (left) and HST NICMOS (right). The compact radio components can be seen in the MERLIN radio image, with the northern components distorted into arcs. The NICMOS infrared image shows a complete Einstein ring. (Courtesy CLASS.)
There are several other CLASS lenses that are undergoing scrutiny for possible variability, and thus are time-delay friendly. The 1.39 arc-second double CLASS B1600 + 434 (left) [A8] (right), which has the distinction of having an edge-on disk galaxy as a lens, was monitored with the VLA during 1998 and significant variability was detected.
 |  |
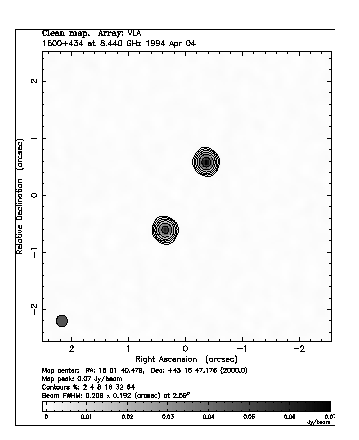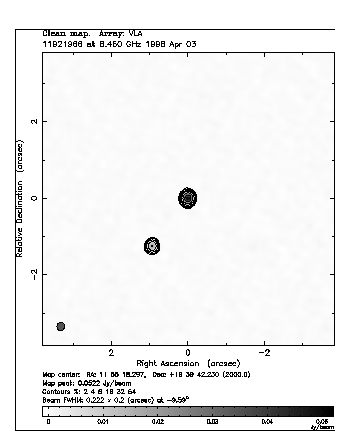Figure 6. VLA X-band images of double image lenses CLASS B1600 + 434 (left) and CLASS B1152 + 199 (right), showing the two compact radio components in each. Note that the axes scales are different in the two maps. (Courtesy CLASS.)
The newly discovered lens CLASS B1152 + 199 [A9] is a 1.6 arc-second double, and has a flat radio spectrum indicative of probable variability. What sets this system apart, however, is that it was detected in x-rays by the ROSAT satellite, and thus is an excellent target for monitoring by AXAF (due to be launched in 2000).
The spectacular 10-image system CLASS B1933 + 503 [A10] (consisting of a triple source imaged into two quads and a double) has an inverted-spectrum core which is split into four images, and was also monitored in 1998. The advantage of this system is that the number of constraints available from the ten images, as well as any measurable substructure in the images, should strongly constrain mass models.
 |  |
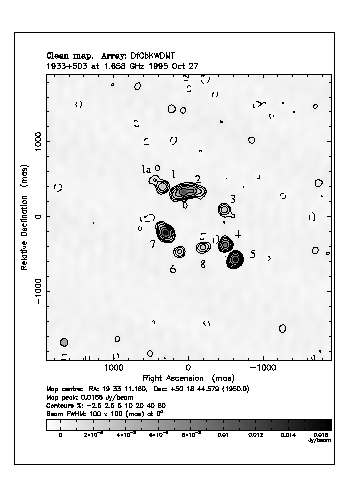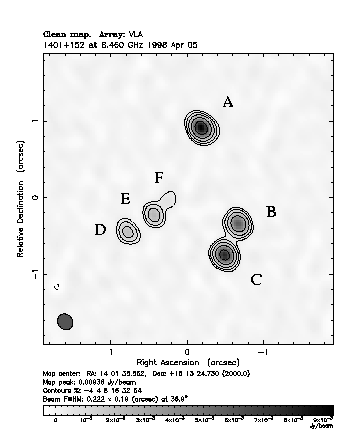Figure 7. At left is the MERLIN image of 10-component lens system CLASS B1933 + 503, with components labeled. Not all components are visible in this L-band map, as they are resolved out by the high resolution of the MERLIN interferometer. At right is shown the quad lens CLASS B1359 + 154, which in addition to gravitationally lensed components A - D, shows radio emission E and F from the lensing galaxy. (Courtesy Dan Marlow, CLASS.)
The final lens shown is the CLASS quadruple image system B1359 + 154, [A9] which was discovered in 1998 in the latest phase of CLASS. In addition to the classic quad morphology (components A - D), emission is also seen from the lensing galaxy itself (components E - F). Furthermore, CLASS B1359 + 154 is like CLASS B1608 + 656 in that the best-fit lens model has two distinct mass components, and single deflector models cannot sufficiently reproduce the observed component configuration or brightnesses (even with an external shear term added).
See also the CASTLES web page for an extensive gallery of optical/IR observations of lens systems.
We note that there are other systems with reported time delays, or that are being monitored for variations, but have missing information (such as the redshift for one or more of the components). These, as well as newly discovered lenses, are sure to produce important information on the Hubble constant and the cosmology of the Univere in the near future.
| Further Reading and Internet Resources: | |
This brief perspective does not do justice to the rich mathematical and astrophysical elegance of the subject. There are, however, a number of excellent reviews available. For a comprehensive, if extremely mathematical, text on all aspects of gravitational lensing, see the excellent book by Schneider [A11]. Blandford and Naryan [A12] have also published an excellent review in the Annual Reviews of Astronomy and Astrophysics series. In the past year some useful comprehensive reviews on the subject have appeared, such as that by Bernardeau [A13], and a 1999 review by Wambsganss in the internet e-Journal Living Reviews in Relativity
There are also a number of internet resources related to the programs described in this article. The CLASS homepage and UPenn archive can be found at
The European and U.K. members of CLASS are part of the CERES network, which has a web site at
With the support of CERES, the puckishly titled ``Workshop on Golden Lenses'' was held at Jodrell Bank, England in June 1997; the proceedings of this conference can be found online at
Although I have taken the liberty of featuring our own work prominently in this perspective, there are a large number of other research groups tackling the problem of gravitational lensing, and many of these groups also have a significant presence on the World Wide Web. For example, the CASTLES group has been carefully compiling imaging and spectroscopic data on all known lenses [A14]. There are a large number of spectacular ground-based and HST images of gravitational lenses posted on the CASTLES web site:
Finally, the Astro-ph preprint archive at Los Alamos Natinonal Laboratory,
is a good source for up-to-date papers in the general field of astrophysics. Another database of note is the NASA Astrophysics Data System (ADS)
for article abstracts as well as for astronomical observations.
| Acknowledgements: | ||
I wish to thank my graduate student David Rusin for letting me nab his succinct summary of the mathematics of lensing. I would also like to thank him and all the other members of CLASS (especially the graduate students Leon Koopmans and Chris Fassnacht) for allowing me to showcase our work in this perspective. I would also like to thank ahead of time all of my colleagues in this field whose work I have left out for having forebearance with my peculiar choices for referencing. Due to the nature of this article, I have only referred to a few key, topical, or representative papers on the various facets of lensing. Caveat emptor.
| References: | ||
[A1] Peebles, P. J. E. (1993) Principles of Physical Cosmology (Univ. Press, Princeton).
[A2] Weinberg, S. (1972) Gravitation and Cosmology (Wiley, New York).
[A3] Caldwell, R. R., Dave, R. & Steinhardt, P. J. (1998) Phys. Rev. 80, 1582-1585.
[A4] Fassnacht, C. D. (1998) Ph.D. thesis (California Institute of Technology, Pasadena, CA).
[A9] Myers, S. T., Rusin, D., Fassnacht, C. D., Blandford, R. D.,
Pearson, T. J., Readhead, A. C. S., Jackson, N., Browne, I. W. A., Marlow, D.,
Wilkinson, P. N., et al. (1999) Astron. J., in press.
[A10] Sykes, C. M., Browne, I. W. A., Jackson, N., Marlow, D.,
Nair, S., Wilkinson, P. N., Blandford, R. D., Cohen, J.,
Fassnacht, C. D., Hogg, D. W., et al. (1998) Mon. Not. R. Astron. Soc.
301, 310-314.
[A11] Schneider, P., Ehlers, J., & Falco, E. E. (1992)
Gravitational Lenses (Springer, New York).
[A12] Blandford, R. & Narayan, R. (1992)
Annu. Rev. Astron. Astrophys. 30, 311-358.